Historia de las matemáticas para niños

Tablilla de barro babilónica YBC 7289 con anotaciones. La diagonal muestra una aproximación de la raíz cuadrada de 2 en cuatro cifras sexagesimales, que son como seis cifras decimales.
1 + 24/60 + 51/60² + 10/60³ = 1.41421296...

La matemática babilónica se refiere a los conocimientos matemáticos de los pueblos de Mesopotamia (actual Irak), desde los sumerios hasta la caída de Babilonia en el 539 a. C. Se le llama babilónica por la importancia de Babilonia como centro de estudio. Más tarde, estas matemáticas se unieron con las griegas y egipcias para formar las matemáticas helenísticas. Bajo el Imperio árabe, Bagdad en Mesopotamia volvió a ser un centro importante para las matemáticas islámicas.

Tenemos muchos textos de matemática babilónica, principalmente de dos épocas: la Antigua Babilonia (1830-1531 a. C.) y el seléucida (últimos siglos a. C.). El contenido de estas matemáticas se mantuvo casi igual por unos dos mil años. A diferencia de las pocas fuentes de matemática egipcia, conocemos la matemática babilónica gracias a unas 400 tablillas de arcilla descubiertas en 1850. Estas tablillas, escritas en escritura cuneiforme, se grababan en arcilla húmeda y luego se endurecían.

Las primeras pruebas de matemáticas escritas vienen de los antiguos sumerios, la primera civilización en Mesopotamia. Los sumerios desarrollaron un sistema complejo de metrología (medidas) desde el 3000 a. C. Desde el 2500 a. C., escribieron tablas de multiplicar en tablillas de arcilla y resolvieron problemas de geometría y división. Los primeros signos de los números babilónicos también son de esa época.

La mayoría de las tablillas de arcilla encontradas son de 1800 a 1600 a. C. y tratan temas como fracciones, álgebra, ecuaciones de segundo y tercer grado, y el cálculo de números regulares recíprocos (ver Plimpton 322). También incluyen tablas de multiplicar y métodos para resolver ecuaciones lineales y ecuaciones cuadráticas. La tablilla babilónica YBC 7289 muestra una aproximación de la raíz cuadrada de 2 con mucha precisión. Las matemáticas babilónicas usaban un sistema de numeración sexagesimal (base 60). De ahí viene que un minuto tenga 60 segundos, una hora 60 minutos, y un círculo 360 grados. A diferencia de egipcios, griegos y romanos, los babilonios tenían un verdadero sistema de valor posicional, donde la posición de un dígito cambiaba su valor, como en nuestro sistema decimal de numeración. Sin embargo, no tenían un símbolo para la coma decimal, por lo que el valor exacto de un número se deducía del contexto.

Papiro de Moscú.

La matemática egipcia se desarrolló en el Antiguo Egipto y fue una de las ciencias más avanzadas allí. Después del periodo helenístico, el griego reemplazó al egipcio como idioma de los estudiosos, y las matemáticas egipcias se mezclaron con las griegas y babilónicas para formar la matemática helénica. Más tarde, bajo la influencia árabe, el árabe se convirtió en el idioma de los estudiosos egipcios, y las matemáticas continuaron como parte de las matemáticas islámicas.

El texto matemático más antiguo que se ha encontrado es el papiro de Moscú, del Imperio Medio de Egipto (hacia 2000-1800 a. C.). Como muchos textos antiguos, contiene "problemas con palabras" o "problemas con historia", que parecen ser para entretener. Un problema importante en este papiro muestra cómo calcular el volumen de un tronco de pirámide: "Si te dicen: una pirámide truncada [de base cuadrada] de 6 de altura vertical, por 4 en la base [base inferior] y 2 en lo alto [base superior]. Haces el cuadrado de 4 y resulta 16. Doblas 4 y resulta 8. Haces el cuadrado de 2 y resulta 4. Sumas el 16, el 8 y el 4 y resulta 28. Tomas un tercio de 6 y resulta 2. Tomas 28 dos veces y resulta 56. Mira, es 56. Encontrarás lo correcto." Otro conjunto de reglas en el papiro es para calcular el volumen de una esfera.

El papiro de Rhind (hacia 1650 a. C.) es otro texto matemático egipcio clave, un manual de aritmética y geometría. Contiene fórmulas para calcular áreas y métodos para multiplicar, dividir y trabajar con fracciones. También muestra conocimientos sobre números compuestos y primos, media aritmética, geométrica y armónica, y una idea simple de la criba de Eratóstenes y la teoría de números perfectos (como el número 6). El papiro también explica cómo resolver ecuaciones lineales de primer orden, así como series aritméticas y series geométricas.

Además, tres elementos geométricos del papiro de Rhind sugieren los inicios de la geometría analítica: cómo obtener una aproximación de con un error pequeño; un intento antiguo de cuadrar el círculo; y el uso más antiguo conocido de un tipo de cotangente. El papiro también dice: "Reglas para estudiar la naturaleza y para comprender todo lo que existe, todo misterio, todo secreto."

Finalmente, el papiro de Berlín (hacia 1300 a. C.) muestra que los antiguos egipcios podían resolver una ecuación cuadrática.

Curiosamente, los papiros más recientes muestran una disminución en los conocimientos, que se reducen a procedimientos prácticos de cálculo y medida. Este era el estado de las matemáticas egipcias cuando los griegos entraron en contacto con ellas.

Se acredita a los pitagóricos la primera demostración general del teorema de Pitágoras.

La matemática griega, o matemática helénica, es la matemática escrita en griego desde el 600 a. C. hasta el 300 d. C. Los matemáticos griegos vivían en ciudades por todo el Mediterráneo Oriental, desde Italia hasta el Norte de África, unidos por un idioma y cultura comunes. Las matemáticas griegas después de Alejandro Magno a veces se llaman matemáticas helenísticas.

Las matemáticas griegas eran más avanzadas que las de culturas anteriores. Todos los registros de matemáticas pre-helénicas muestran el uso del razonamiento inductivo, es decir, usar observaciones repetidas para establecer reglas generales. Los matemáticos griegos, en cambio, usaban el razonamiento deductivo. Los griegos usaban la lógica para sacar conclusiones, o teoremas, a partir de definiciones y axiomas. La idea de las matemáticas como una red de teoremas basados en axiomas se ve claramente en los Elementos de Euclides (hacia el 300 a. C.).

Se cree que las matemáticas griegas comenzaron con Tales (hacia 624 a. C. - 546 a. C.) y Pitágoras (hacia 582 a. C. - 507 a. C.). Aunque su influencia puede ser discutida, probablemente se inspiraron en las matemáticas egipcias, mesopotámicas e indias. Según la leyenda, Pitágoras viajó a Egipto para aprender matemáticas, geometría y astronomía de los sacerdotes egipcios.

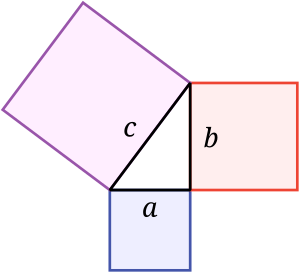
Tales usó la geometría para resolver problemas como calcular la altura de las pirámides y la distancia de los barcos desde la orilla. A Pitágoras se le atribuye la primera demostración del teorema que lleva su nombre, aunque el teorema ya existía antes. En su comentario sobre Euclides, Proclo dice que Pitágoras formuló el teorema y construyó ternas pitagóricas de forma algebraica antes que geométrica. La Academia de Platón tenía como lema "Que no pase nadie que no sepa Geometría".

Los Pitagóricos demostraron la existencia de números irracionales. Eudoxio (408 al 355 a. C.) desarrolló el método exhaustivo, un precursor de la integración moderna. Aristóteles (384 al 322 a. C.) fue el primero en escribir las leyes de la lógica. Euclides (hacia el 300 a. C.) dio el ejemplo más antiguo de la metodología matemática actual, con definiciones, axiomas, teoremas y demostraciones. Euclides también estudió las cónicas. Su libro Elementos recopila toda la matemática de su época. En los Elementos se tratan problemas fundamentales de la matemática, siempre con lenguaje geométrico. Además de teoremas de geometría, también aborda problemas aritméticos, algebraicos y de análisis matemático. Los Elementos incluyen una demostración de que la raíz cuadrada de dos es un número irracional y otra sobre la infinitud de los números primos. La Criba de Eratóstenes (hacia 230 a. C.) se usó para descubrir números primos.

Arquímedes de Siracusa (hacia 287-212 a. C.) usó el método exhaustivo para calcular el área bajo un arco de parábola usando la suma de una serie infinita y dio una aproximación muy precisa de pi. También estudió la espiral, fórmulas para el volumen de superficies de revolución y un sistema ingenioso para expresar números muy grandes.

Muchos matemáticos griegos hicieron sus propios estudios y aportaron descubrimientos al conocimiento general de las matemáticas y otras ciencias. Además, hicieron algo fundamental: convirtieron las matemáticas en una ciencia racional, es decir, una ciencia lógica, rigurosa, basada en axiomas y postulados.

Los nueve capítulos sobre el arte matemático.

En el 212 a. C., el emperador Qin Shi Huang ordenó quemar todos los libros de fuera del estado de Qin. No todos obedecieron, pero por esta razón se sabe muy poco sobre la matemática en la China antigua. El libro de matemáticas más antiguo que sobrevivió fue el I Ching, que usa trigramas y hexagramas con fines filosóficos, matemáticos y místicos. Estos objetos matemáticos están hechos de líneas enteras o divididas llamadas yin (femenino) y yang (masculino).

La obra más antigua sobre geometría en China viene del canon filosófico mohista, hacia el 330 a. C., recopilado por los seguidores de Mozi (470-390 a. C.). El Mo Jing describió varios aspectos de la física y también algo de matemáticas.

Después de la quema de libros, la dinastía Han (202 a. C.–220 d. C.) produjo obras matemáticas que probablemente se basaron en trabajos perdidos. La más importante es Los nueve capítulos sobre el arte matemático, cuyo título completo apareció hacia el 179 d. C., pero ya existía antes en partes. La obra contiene 246 problemas que tratan sobre agricultura, negocios, usos geométricos para medir pagodas, ingeniería, agrimensura y conceptos de triángulos rectángulos y π (pi). También usa el principio de Cavalieri sobre volúmenes, más de mil años antes de que Cavalieri lo formulara en Occidente. Se crearon pruebas sobre el Teorema de Pitágoras y una forma matemática de la eliminación de Gauss-Jordan. Liu Hui hizo un comentario sobre esta obra en el siglo III.

En resumen, las obras matemáticas del astrónomo e inventor Zhang Heng (78–139 d. C.) del período Han también contenían una fórmula para , diferente de los cálculos de Liu Hui. Zhang Heng usó su fórmula de para encontrar volúmenes esféricos. También están los trabajos del matemático y teórico de la música Jing Fang (78–37 a. C.); usando la coma pitagórica, Jing notó que 53 quintas justas se acercan a 31 octavas. Esto llevó al descubrimiento del temperamento igual, que divide la octava en 53 partes iguales, y no se volvió a calcular con tanta precisión hasta el siglo XVII por el alemán Nicholas Mercator.

Los chinos también usaron diagramas combinatorios complejos como el cuadrado mágico y el círculo mágico, descritos en tiempos antiguos y mejorados por Yang Hui (1238–1398 d. C.).

En el siglo V, Zu Chongzhi de las dinastías meridionales y septentrionales calculó el valor de con siete decimales, siendo el valor más exacto de durante casi 1000 años.

Teorema de Brahmagupta.

La matemática india fue muy importante para la cultura occidental antes del Renacimiento, especialmente por sus cifras, incluyendo el número cero (0), para indicar la ausencia de una unidad en la notación posicional.

Las primeras matemáticas conocidas en la historia de la India son de 3000-2600 a. C., de la cultura del valle del Indo (civilización Harappa) en el norte de la India y Pakistán. Esta civilización desarrolló un sistema de medidas y pesos uniforme que usaba el sistema decimal, una tecnología avanzada con ladrillos para representar razones, calles en ángulos rectos y formas geométricas como cuboides, barriles, conos, cilindros y diseños de círculos y triángulos. Los instrumentos matemáticos incluían una regla decimal precisa, estructuras para medir el horizonte y el cielo, y un instrumento para medir la posición de las estrellas para la navegación. La escritura de Harappa no ha sido descifrada, por lo que se sabe poco de sus matemáticas escritas. Hay pruebas arqueológicas que sugieren que esta civilización usaba un sistema de numeración de base octal y conocía el valor de π.

Sin embargo, fue durante el período clásico (siglos I al VIII) cuando los matemáticos indios alcanzaron su madurez. Antes de esto, los hindúes tuvieron contacto con el mundo griego. La campaña de Alejandro Magno en la India fue en el siglo IV a. C.. Además, la expansión del budismo en China y del mundo árabe aumentó los contactos de la India con el exterior. A pesar de esto, las matemáticas hindúes se desarrollaron de forma original, enfocándose más en el cálculo numérico que en la lógica rigurosa.

Los avances en matemática india después de los Sulba Sutras son los Siddhantas, tratados astronómicos del período Gupta (siglos IV y V d. C.) con fuerte influencia helénica. Son importantes porque contienen las primeras relaciones trigonométricas basadas en una semicuerda, como en la trigonometría moderna, en lugar de una cuerda completa, como en la trigonometría ptolemaica. Con algunas alteraciones y errores de traducción, las palabras «seno» y «coseno» vienen del sánscrito jiya y kojiya.

El Suria-sidhanta (hacia el año 400) introdujo las funciones trigonométricas de seno, coseno y arcoseno, y estableció reglas para determinar las trayectorias de los astros que coinciden con sus posiciones actuales. Los ciclos cosmológicos del texto, copias de trabajos anteriores, correspondían a un año sideral medio de 365.2563627 días, solo 1.4 segundos más que el valor actual. Este trabajo fue traducido del árabe al latín en la Edad Media.

Aryabhata.

En el siglo V, Aryabhata escribió el Aryabhatiya, un libro para complementar las reglas de cálculo en astronomía y medida. Escrito en verso, no tenía un rigor lógico estricto. Aunque casi la mitad de sus entradas son incorrectas, en el Aryabhatiya aparece por primera vez el sistema decimal posicional. Siglos después, el matemático árabe Abu Rayhan Biruni lo describió como "una mezcla de guijarros comunes y cristales valiosos". En 499, Aryabhata introdujo la función verseno, produjo las primeras tablas trigonométricas del seno, desarrolló técnicas y algoritmos de álgebra y resolvió ecuaciones lineales, además de cálculos astronómicos basados en un sistema geocéntrico. Una traducción al árabe de su Ariabhatiya estuvo disponible desde el siglo VIII, seguida de una traducción al latín en el siglo XIII. También calculó el valor de π con once decimales (3,14159265359).

En el siglo VII, Brahmagupta identificó el teorema de Brahmagupta, la identidad de Brahmagupta y la fórmula de Brahmagupta. Por primera vez en Brahma-sphuta-siddhanta, explicó claramente los dos usos del número 0: como símbolo para rellenar un espacio en el sistema posicional y como una cifra. También explicó el sistema de numeración indoarábigo. Gracias a una traducción de este texto indio (hacia el 770), las matemáticas islámicas tuvieron acceso a este sistema, que luego adaptaron usando los numerales arábigos. Los estudiantes árabes llevaron este conocimiento a Europa hacia el siglo XII, y finalmente reemplazó los sistemas de numeración anteriores en todo el mundo. En el siglo X, un comentario de Jalaiuda sobre la obra de Pingala incluyó un estudio de la sucesión de Fibonacci y del triángulo de Pascal, y describió la formación de una matriz.

En el siglo XII, Bhaskara II estudió varias áreas de las matemáticas. Sus trabajos describen el concepto preliminar de infinitesimal y coeficiente diferencial. También estableció el teorema de Rolle (un caso especial del teorema del valor medio), estudió la ecuación de Pell, e investigó la derivada de la función seno. Hasta qué punto sus aportes anticiparon la invención del cálculo es un tema de debate entre los historiadores.

Desde el siglo XII, Mádhava, fundador de la Escuela de Kerala, encontró la llamada serie de Madhava-Leibniz y, usando 21 términos, calculó el valor del número π a 3,14159265359. Mádhava también encontró la serie de Madhava-Gregory para el arcotangente, la serie de potencias Madhava-Newton para el seno y el coseno, así como aproximaciones de Taylor para estas funciones. En el siglo XVI, Jyesthadeva recopiló muchos desarrollos y teoremas de la Escuela de Kerala en los Yukti-bhāṣā. Sin embargo, la Escuela no formuló una teoría sistemática de la derivada o la integración, y no hay pruebas directas de que sus resultados se transmitieran fuera de Kerala.

Los avances en matemáticas y otras ciencias se detuvieron en la India después de la conquista musulmana de la India.

Quipukamayuq con su quipu y una yupana, los principales instrumentos que usaron los incas en matemáticas.

Las matemáticas de los incas se refieren a los conocimientos numéricos y geométricos, y los instrumentos que desarrollaron y usaron en el imperio inca antes de la llegada de los españoles. Se caracterizan principalmente por su habilidad para calcular en el ámbito económico. Los quipus y yupanas muestran la importancia que tuvo la aritmética en la administración del estado inca. Esto se tradujo en una aritmética sencilla pero eficaz para fines contables, basada en el sistema decimal; conocieron el cero, y dominaron la suma, la resta, la multiplicación y la división. Su matemática era principalmente práctica, usada para la gestión, estadísticas y medición. No era una matemática teórica como la griega, sino útil para las necesidades de una administración centralizada.

Además, la construcción de caminos, canales y monumentos, así como el diseño de ciudades y fortalezas, requirió el desarrollo de una geometría práctica. Esta fue esencial para medir longitudes y superficies, y para el diseño arquitectónico. También desarrollaron importantes sistemas de medición de longitud y capacidad, usando partes del cuerpo humano como referencia. Además, emplearon objetos o acciones que permitían apreciar el resultado de otra manera, pero de forma útil y efectiva.

Numeración maya.

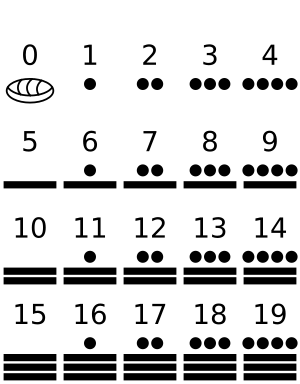
Los mayas usaban un sistema de numeración vigesimal (de base 20) con una raíz mixta, similar a otras civilizaciones de Mesoamérica. El sistema numérico de rayas y puntos, base de la numeración maya, se usaba en Mesoamérica desde el 1000 a. C. Los mayas lo adoptaron en el Preclásico Tardío y añadieron el símbolo para el cero. Esta podría ser la aparición más temprana conocida del concepto de cero explícito en el mundo, aunque es posible que el sistema babilónico lo precediera. El primer uso explícito del cero se registró en monumentos del 357 d. C. Al principio, el cero servía como notación posicional, indicando la ausencia de un conteo específico en el calendario. Más tarde, se convirtió en un número que se podía usar para cálculos y se incluyó en textos jeroglíficos por más de mil años, hasta que su uso fue eliminado por los españoles.

En el sistema de numeración de base, un punto representa la unidad. Dos, tres y cuatro puntos representan 2, 3 y 4, y una raya horizontal representa 5. En el período Posclásico, el símbolo de una concha (o caracol) representaba el cero; en el período Clásico se usaron otros símbolos. Los mayas podían escribir cualquier número del 0 al 19 combinando estos símbolos. El valor exacto de un número se determinaba por su posición vertical; al subir una posición, el valor básico de la unidad se multiplicaba por veinte. Así, el símbolo más bajo representaba las unidades, el siguiente símbolo (en la segunda posición) representaba una multiplicación por veinte de la unidad, y el símbolo en la tercera posición representaba una multiplicación por 400, y así sucesivamente. Por ejemplo, el número 884 se escribe con cuatro puntos en el nivel más bajo (4 x 1), cuatro puntos en el nivel siguiente (4 x 20), y dos puntos en el tercer nivel (2 x 400). Con este sistema, los mayas podían escribir números muy grandes. Las sumas sencillas se hacían sumando los puntos y rayas en dos columnas, y el resultado se ponía en una tercera columna.

Codex Vigilanus, con los primeros números arábigos.

Página del Compendio de cálculo por compleción y comparación escrito por Al-Juarismi.

La matemática islámica, también conocida como matemática árabe o matemática musulmana, creció mucho a medida que los musulmanes conquistaban nuevos territorios. El imperio islámico se expandió rápidamente por las orillas del Mediterráneo, desde Persia (Irán) hasta los Pirineos.

El imperio islámico, que abarcaba Oriente Medio, Asia Central, África del Norte, la Península Ibérica y parte de la India, hizo grandes aportes a las matemáticas en el siglo VIII. Aunque la mayoría de los textos islámicos sobre matemáticas se escribieron en árabe, no todos fueron escritos por árabes. Así como el griego se usaba en el mundo helenístico, el árabe era el idioma escrito de los intelectuales no árabes en el mundo islámico de esa época. Junto con los árabes, muchos otros matemáticos islámicos importantes eran persas.

En el siglo IX, Al-Juarismi escribió varios libros importantes sobre los números arábigos y sobre cómo resolver ecuaciones. Su libro Sobre los cálculos con números arábigos, escrito alrededor del año 825, junto con el trabajo de Al-Kindi, fueron clave para que las matemáticas árabes y los números arábigos se conocieran en Occidente. La palabra algoritmo viene de la latinización de su nombre, algoritmi, y la palabra álgebra del título de uno de sus trabajos, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (Compendio de cálculo por compleción y comparación). A Al-Juarismi a menudo se le llama "el padre del álgebra" por sus importantes contribuciones. Explicó detalladamente cómo resolver ecuaciones de segundo grado con soluciones positivas, y fue el primero en enseñar el álgebra en sus formas más básicas. También introdujo el método fundamental de "reducción" y "balance", que se refiere a mover términos restados al otro lado de una ecuación, o cancelar términos iguales en lados opuestos. Esta operación fue descrita originalmente por Al-Juarismi como al-jabr. Su álgebra no era solo una serie de problemas sin resolver, sino una explicación que comenzaba con las condiciones básicas para todos los tipos posibles de ecuaciones, que luego serían estudiadas.

El desarrollo posterior del álgebra vino de la mano de Al-Karaji. En su tratado al-Fakhri extendió la metodología para incluir potencias y raíces de cantidades desconocidas. La primera demostración por inducción matemática conocida aparece en un libro escrito por Al-Karaji en el 1000 d. C., donde demuestra el teorema del binomio, el triángulo de Pascal, y la suma de cubos integrales. El historiador de las matemáticas, F. Woepcke, elogió a Al-Karaji por haber sido "el primero en introducir la teoría del cálculo algebraico." También en el siglo X Abul Wafa tradujo las obras de Diofanto al árabe y desarrolló la función tangente. Ibn al-Haytham fue el primer matemático en deducir la fórmula de la suma de las ecuaciones cuárticas, usando un método que puede generalizarse para determinar la fórmula general de la suma de cualquier potencia entera. Desarrolló una integración para calcular el volumen de un paraboloide y pudo generalizar sus resultados para las integrales de polinomios de más de cuarto grado. Incluso se acercó mucho a la fórmula general de la integral de polinomios, aunque no le interesaban los polinomios de grado mayor que cuatro.

A finales del siglo XI, Omar Khayyam escribió Discusiones sobre las dificultades en Euclides, un libro sobre los defectos en los Elementos de Euclides, especialmente el postulado de las paralelas, y sentó las bases de la geometría analítica y la geometría no euclídea. También fue el primero en encontrar la solución geométrica a la ecuación cúbica e influyó en la reforma del calendario.