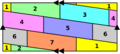
Teorema de los cuatro colores para niños
El Teorema de los Cuatro Colores es una idea fascinante en el mundo de las matemáticas, específicamente en una rama llamada teoría de grafos. Este teorema nos dice algo muy interesante sobre cómo podemos colorear mapas.
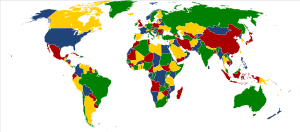
Imagina que tienes un mapa con diferentes países o regiones. El teorema de los cuatro colores afirma que siempre puedes colorear cualquier mapa geográfico usando solo cuatro colores diferentes (o menos). La única regla es que dos regiones que se tocan por un borde (no solo por una esquina) no pueden tener el mismo color.
A veces, con solo tres colores es suficiente para un mapa sencillo. Pero hay mapas más complejos donde se necesita un cuarto color. Esto ocurre, por ejemplo, cuando una región está rodeada por un número impar de regiones que se tocan entre sí, formando un círculo.
Mucho antes de que se demostrara el teorema de los cuatro colores, ya se había probado el Teorema de los Cinco Colores. Este teorema, que es más sencillo de demostrar, dice que cinco colores son suficientes para colorear cualquier mapa. Fue demostrado en el siglo XIX por un matemático llamado Heawood.
El desafío de los cuatro colores, conocido como el "problema del mapa de cuatro colores", fue propuesto por primera vez en 1852 por un estudiante llamado Francis Guthrie. La idea se hizo muy conocida cuando el matemático Arthur Cayley mencionó que había intentado resolverlo en 1878. Finalmente, el teorema fue demostrado a mediados de los años 70 por Kenneth Appel y Wolfgang Haken.
Contenido
¿Cómo funciona el teorema de los cuatro colores?
Para entender bien el teorema, hay algunas cosas importantes que considerar:
Regiones continuas
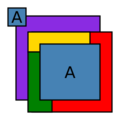
Cada "país" o región en el mapa debe ser una sola pieza, es decir, una región continua. En el mundo real, algunos países tienen partes separadas (como Alaska, que es parte de Estados Unidos pero no está conectada directamente). Si permitiéramos regiones no continuas, cuatro colores podrían no ser suficientes. Por ejemplo, si un país tiene dos partes separadas y cada una de esas partes toca a otras cuatro regiones diferentes, se necesitarían más de cuatro colores para que todas las partes del mismo país tuvieran el mismo color.
Mapas y grafos
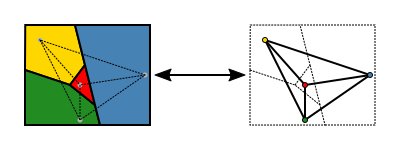
El teorema de los cuatro colores se puede entender mejor usando la teoría de grafos. Piensa en cada región de un mapa como un "punto" o vértice. Si dos regiones se tocan, dibujamos una "línea" o arista entre sus vértices correspondientes.
Cuando hacemos esto, creamos un dibujo llamado grafo. Este grafo es "plano", lo que significa que puedes dibujarlo en una superficie sin que las líneas se crucen. El problema de colorear un mapa se convierte entonces en el problema de colorear los vértices de este grafo. La regla es que dos vértices conectados por una línea no pueden tener el mismo color.
Así, el Teorema de los Cuatro Colores se puede expresar de esta manera en la teoría de grafos:
- Si tienes un grafo plano, puedes colorear sus vértices con un máximo de cuatro colores, de modo que no haya dos vértices conectados que tengan el mismo color.
Historia del descubrimiento
La idea del teorema de los cuatro colores comenzó como una suposición, o conjetura.
Los primeros pasos
En 1852, Francis Guthrie, un estudiante, formuló la conjetura. Él y su hermano, Frederick, intentaron probarla, pero no lo lograron. Incluso el famoso matemático William Rowan Hamilton recibió la conjetura, pero tampoco pudo resolverla.
En 1879, Alfred Bray Kempe anunció que había encontrado una demostración. Sin embargo, en 1890, otro matemático, Percy John Heawood, descubrió un error en la prueba de Kempe. Aunque Heawood no pudo probar la conjetura de los cuatro colores, sí logró demostrar que con cinco colores siempre se podía colorear cualquier mapa. Esto se conoce como el Teorema de los Cinco Colores.
La demostración con ordenador
La conjetura de los cuatro colores fue finalmente demostrada en 1976 por Kenneth Appel y Wolfgang Haken. Lo más sorprendente de su demostración fue que utilizaron un ordenador para verificar una gran cantidad de casos.
Esta forma de demostrar un teorema generó mucha discusión entre los matemáticos. Algunos no estaban de acuerdo porque la prueba era tan larga y compleja que una persona no podía revisarla completamente a mano. Había que confiar en que el programa de ordenador, el compilador y el propio ordenador funcionaran perfectamente.
Además, algunos matemáticos consideraron que la prueba carecía de "elegancia". Una crítica famosa de la época decía que "una buena prueba matemática es como un poema, ¡pero esto es una guía telefónica!".
Mejoras y verificaciones posteriores
Desde la demostración original, se han hecho mejoras. En 1996, un equipo de matemáticos (Neil Robertson, Daniel P. Sanders, Paul Seymour y Robin Thomas) creó un algoritmo más eficiente que redujo el número de casos a comprobar a 633. Aunque sigue siendo un número grande, es una mejora. Esta nueva prueba también necesita ser ejecutada por un ordenador.
En 2005, Georges Gonthier verificó el teorema usando un programa informático especial llamado "asistente de pruebas" (Coq). Esto significó que ya no era necesario confiar en varios programas diferentes, sino solo en el núcleo de este asistente de pruebas.
¿Por qué no más de cuatro colores?
Las ideas detrás de la demostración del teorema son complejas, pero se basan en algunos principios clave:
- Grafos triangulares: Los matemáticos demostraron que si el teorema funciona para mapas donde todas las regiones son como triángulos (es decir, tienen tres bordes), entonces funciona para todos los mapas.
- Vértices de bajo grado: En cualquier grafo plano, siempre debe haber al menos un vértice (una región) que esté conectado a 5 o menos otras regiones.
- El argumento de Kempe: Kempe intentó demostrar que no puede existir un mapa que necesite 5 colores. Su idea era que si existiera un mapa así, se podría encontrar una región que, al quitarla, permitiría colorear el resto del mapa con 4 colores. Luego, al intentar volver a poner la región, se usarían unas "cadenas de Kempe" (caminos de colores alternos) para reorganizar los colores de las regiones vecinas y así poder colorear la región original con uno de los cuatro colores. Aunque su argumento tenía un fallo para el caso de 5 vecinos, fue la base para la demostración posterior.
Falsas refutaciones
El Teorema de los Cuatro Colores ha sido famoso por atraer muchos intentos de pruebas y refutaciones incorrectas a lo largo de su historia. Al principio, algunos periódicos se negaron a informar sobre la prueba de Appel-Haken, por miedo a que resultara ser falsa, como muchas otras antes.
Algunas supuestas pruebas, como las de Kempe y Tait, fueron examinadas por el público durante más de una década antes de que se demostrara que estaban equivocadas. Pero muchas otras, hechas por aficionados, nunca llegaron a publicarse.
[[multiple image | align = right | image1 = 4CT Non-Counterexample 1.svg | width1 = 150 | alt1 = | caption1 = | image2 = 4CT Non-Counterexample 2.svg | width2 = 150 | alt2 = | caption2 = | footer = En el primer mapa, que parece necesitar más de cuatro colores, la sustitución de las regiones rojas con cualquiera de los otros cuatro colores no funcionaría. Sin embargo, los colores pueden reordenarse, como se ve en el segundo mapa, para usar solo cuatro. ]]
Generalmente, los intentos de "contraejemplos" (ejemplos que supuestamente demuestran que el teorema es falso) más sencillos intentan crear una región que toque a todas las demás. Esto obligaría a colorear las regiones restantes con solo tres colores. Como el teorema es cierto, esto siempre es posible. Sin embargo, la persona que dibuja el mapa se concentra en la región grande y no se da cuenta de que las regiones restantes sí pueden colorearse con tres colores.
Otros intentos de refutación fallan porque no cumplen las reglas del teorema. Por ejemplo, usan una región que tiene varias partes desconectadas, o permiten que regiones del mismo color se toquen solo en un punto (cuando la regla es que no se toquen por un borde).
Galería de imágenes
-
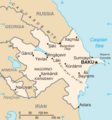
Ejemplo de un mapa de Azerbaiyán con regiones no continuas.
-
Este mapa, con regiones no continuas (las dos "A" pertenecen al mismo país), necesitaría cinco colores.
-
Uniendo las flechas simples y las flechas dobles, se obtiene un toro con siete regiones colindantes, con lo que son necesarios siete colores.
-
Esta construcción muestra un toro dividido en el máximo de siete regiones, cada una de las cuales toca a las otras.
Véase también
En inglés: Four color theorem Facts for Kids
