Pirámide (geometría) para niños

Datos para niños Pirámides
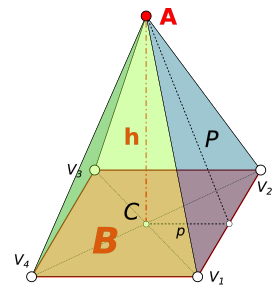Pirámide recta de base cuadrada y sus principales elementos
Caras	n + 1
Polígonos que forman las caras	Base poligonal y triángulos laterales
Aristas	2n
Vértices	n + 1
Grupo de simetría	Cnv
Poliedro dual	Autodual
Símbolo de Schläfli	∨{n}
Propiedades
Poliedro convexo
Desarrollo

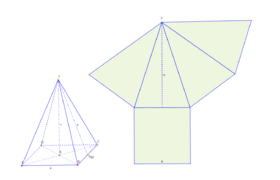En geometría, una pirámide es una figura de tres dimensiones. Está formada por una base que es un polígono (una figura plana con lados rectos, como un cuadrado o un triángulo). Sus lados, llamados caras laterales, son triángulos que se unen en un punto en la parte superior. Este punto se llama ápice o cúspide.

Las pirámides son poliedros, lo que significa que son cuerpos geométricos con caras planas. El número de lados de la base de una pirámide determina cuántas caras triangulares tendrá. Por ejemplo, una pirámide con una base cuadrada tendrá cuatro caras triangulares.

¿Qué es una pirámide en geometría?

Una pirámide es un cuerpo geométrico que se forma al unir todos los puntos de un polígono (la base) con un punto que está fuera del plano de ese polígono (el ápice). Piensa en las famosas pirámides de Egipto; son un ejemplo de pirámides con base cuadrada.

Partes de una pirámide

Para entender mejor una pirámide, veamos sus partes principales:

• Base (B): Es el polígono que forma la parte inferior de la pirámide. Puede ser un cuadrado, un triángulo, un pentágono, etc.
• Vértice de la pirámide (A): También conocido como ápice o cúspide. Es el punto más alto de la pirámide, donde se unen todas las caras triangulares.
• Altura (h): Es la distancia perpendicular desde el ápice hasta el centro de la base. Imagina una línea recta que baja desde la punta de la pirámide hasta el medio de su base.
• Apotema de la pirámide (P): Es la altura de una de las caras triangulares laterales. Va desde el ápice hasta el punto medio de uno de los lados de la base.
• Apotema de la base (p): Es la distancia desde el centro de la base hasta el punto medio de uno de sus lados.
• Arista lateral: Es la línea que une cada vértice de la base con el ápice de la pirámide.
• Cara lateral: Son los triángulos que forman los lados de la pirámide.

Tipos de pirámides

Las pirámides se pueden clasificar de diferentes maneras, según la forma de su base o la posición de su ápice.

Pirámides recta (1) y oblicuas: (2) aguda, (3) rectángula y (4) obtusa

¿Cómo se clasifican las pirámides por la posición de su ápice?

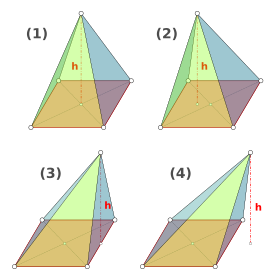
• Pirámide recta: Si el ápice está justo encima del centro de la base. Las pirámides de Egipto son un buen ejemplo.
• Pirámide oblicua: Si el ápice no está directamente sobre el centro de la base. Parece que está inclinada.
• Pirámide aguda: La proyección del ápice cae dentro de la base.
• Pirámide en ángulo recto (o rectangular): La proyección del ápice cae sobre un lado o un vértice de la base.
• Pirámide obtusa: La proyección del ápice cae fuera de la base.

¿Cómo se clasifican las pirámides por la forma de sus caras?

• Pirámide de base regular: Su base es un polígono regular (todos sus lados y ángulos son iguales, como un cuadrado o un triángulo equilátero).
• Pirámide regular: Es una pirámide recta y de base regular. Todas sus caras laterales son triángulos idénticos. Ejemplos son el tetraedro (pirámide triangular), la pirámide cuadrada y la pirámide pentagonal.
• Pirámide convexa: Su base es un polígono convexo (todos sus ángulos interiores son menores de 180 grados).
• Pirámide cóncava: Su base es un polígono cóncavo (tiene al menos un ángulo interior mayor de 180 grados).

Pirámides rectas con base regular

Las pirámides rectas con base regular son las más comunes. Sus caras laterales son triángulos isósceles (tienen dos lados iguales).

• La pirámide triangular es un tetraedro regular si todas sus caras son triángulos equiláteros. Es uno de los sólidos platónicos, que son figuras geométricas perfectas.
• Las pirámides cuadradas y pentagonales también pueden ser especiales si están hechas de polígonos regulares.

Pirámide pentagrámica

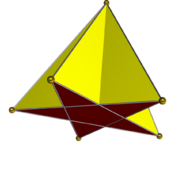
Las pirámides estrelladas son pirámides rectas cuya base es un polígono estrellado. Por ejemplo, una pirámide pentagrámica tiene una base con forma de estrella de cinco puntas.

¿Cómo calcular el área de una pirámide?

Para calcular el área total de una pirámide, necesitamos sumar el área de su base y el área de todas sus caras laterales.

Área de la base (A_b)

Si la base es un polígono regular, puedes dividirlo en triángulos. El área de la base se calcula con la fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A_b = \frac{n}{4} \ l^2 \cdot \cot \left ( \frac{\pi}{n} \right ) Donde n es el número de lados de la base y l es la longitud de un lado de la base.

Área lateral (A_l)

El área lateral es la suma de las áreas de todas las caras triangulares. Como son triángulos, su área es (base x altura) / 2. En este caso, la "altura" de cada triángulo es la apotema de la pirámide (a_p). 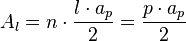Donde n es el número de caras laterales, l es la longitud de un lado de la base, y p es el perímetro de la base.

Teorema de Pitágoras:
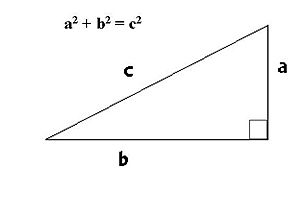
Altura de la pirámide: h = a.
Apotema de la base: a_b = b.
Apotema de la pirámide: a_p = c

Puedes encontrar la apotema de la pirámide (a_p) usando el teorema de Pitágoras si conoces la altura de la pirámide (h) y la apotema de la base (a_b):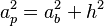

Área total (A)

El área total de la pirámide es la suma del área de la base y el área lateral: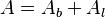

¿Cómo calcular el volumen de una pirámide?

El volumen de una pirámide es la cantidad de espacio que ocupa. Se calcula con una fórmula sencilla que depende del área de su base y de su altura.

La fórmula general para el volumen de cualquier pirámide es: 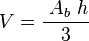Donde A_b es el área de la base y h es la altura de la pirámide.

Esta fórmula fue descubierta por el matemático indio Aryabhata alrededor del año 499 a.C.

Demostración del volumen de una pirámide

Podemos entender por qué la fórmula del volumen es así de forma visual.

Descomposición de un prisma recto de base triangular en tres pirámides del mismo volumen (roja, azul y verde)

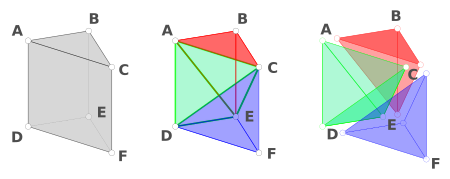
• Usando un prisma triangular:

Imagina un prisma con base triangular. Puedes dividir este prisma en tres pirámides que tienen el mismo volumen. Si el volumen del prisma es "Área de la base x altura", entonces el volumen de cada pirámide es un tercio de eso.

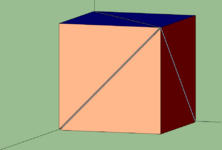
• Usando un cubo:

Cubo dividido en tres pirámides iguales

El mismo cubo una vez descompuesto

También puedes dividir un cubo en tres pirámides iguales. Si tomas un vértice del cubo como el ápice de las pirámides, y las tres caras que se unen a ese vértice como las bases, verás que las tres pirámides tienen el mismo volumen. Como las tres juntas forman el cubo, el volumen de cada pirámide es un tercio del volumen del cubo.

Centro de gravedad de una pirámide

El centro de gravedad de una pirámide (si es uniforme en densidad) se encuentra en su altura. Está a una distancia de la base igual a un cuarto de su altura total. Es decir, si la pirámide mide 12 cm de alto, su centro de gravedad estará a 3 cm de la base.

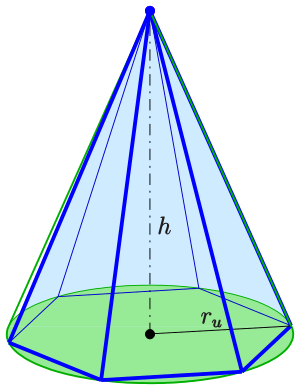
Relación con el cono circular

Pirámide para aproximar un cono

Un cono es como una pirámide con una base circular. Puedes imaginar un cono como una pirámide con una base que tiene un número infinito de lados muy pequeños. A medida que el número de lados de la base de una pirámide regular aumenta, la forma de la base se parece cada vez más a un círculo, y la pirámide se parece cada vez más a un cono. Por eso, la fórmula del volumen del cono es muy similar a la de la pirámide: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V_{\mathrm{Cono}} = \frac 1 3 \pi r_u^2 \cdot h Donde r_u es el radio de la base circular y h es la altura.

Véase también

En inglés: Pyramid (geometry) Facts for Kids

• Tronco de pirámide
• Tetraedro
• Cono
• Bipirámide (cuando dos pirámides se unen por sus bases)