Media geométrica para niños
La media geométrica es un tipo especial de promedio que se usa en matemáticas y estadística. Imagina que tienes varios números. Para encontrar su media geométrica, los multiplicas todos y luego calculas la raíz n-ésima de ese resultado. La "n" es la cantidad de números que tienes.
Esta media es muy útil cuando los datos crecen o cambian de forma multiplicativa, como en las progresiones geométricas, para calcular promedios de porcentajes de crecimiento o para entender el interés compuesto.
Contenido
- Media Geométrica: Un Promedio Especial
- Véase también
Media Geométrica: Un Promedio Especial
La media geométrica es diferente de la media aritmética (el promedio que usas más a menudo, sumando y dividiendo). La media geométrica es ideal para situaciones donde los números se relacionan por multiplicación, no por suma.
¿Cómo se calcula la Media Geométrica?
Para calcular la media geométrica de un grupo de números, sigue estos pasos:
- Multiplica todos los números entre sí.
- Al resultado de esa multiplicación, le sacas la raíz que corresponda a la cantidad de números que multiplicaste.
Por ejemplo, si tienes los números 2 y 18:
- Multiplicas 2 por 18, lo que da 36.
- Como son dos números, calculas la raíz cuadrada de 36, que es 6.
Así, la media geométrica de 2 y 18 es 6.
Otro ejemplo con tres números: 1, 3 y 9.
- Multiplicas 1 x 3 x 9, lo que da 27.
- Como son tres números, calculas la raíz cúbica de 27, que es 3.
La media geométrica de 1, 3 y 9 es 3.
La fórmula general se ve así:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{x} = \sqrt[n]{x_1 \cdot x_2 \cdots x_n}
Donde Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x_1, x_2, \dots, x_n son los números y 
es la cantidad de números.
¿Cuándo usamos la Media Geométrica?
La media geométrica es muy útil cuando comparamos cosas que tienen diferentes escalas de medida.
Comparando Empresas: Un Ejemplo Práctico
Imagina que quieres comparar dos empresas. Una se califica de 0 a 5 por su cuidado del medio ambiente, y la otra de 0 a 100 por su estabilidad económica.
Si usaras la media aritmética, la calificación económica tendría mucho más peso porque sus números son más grandes. Un pequeño cambio en la calificación económica (por ejemplo, de 80 a 90) afectaría mucho más el promedio que un gran cambio en la calificación ambiental (por ejemplo, de 2 a 5).
La media geométrica ayuda a que los cambios porcentuales tengan el mismo efecto, sin importar la escala. Así, un aumento del 20% en la calificación ambiental (de 4 a 4.8) tiene el mismo impacto en la media geométrica que un aumento del 20% en la estabilidad económica (de 60 a 72). Esto hace que la comparación sea más justa.
La Media Geométrica y la Geometría
Esta media tiene un significado visual en la geometría.
- Para dos números, a y b, su media geométrica es la longitud del lado de un cuadrado que tiene la misma área que un rectángulo con lados de longitud a y b.
- Para tres números, a, b y c, su media geométrica es la longitud de la arista de un cubo que tiene el mismo volumen que una caja rectangular (llamada ortoedro) con lados de longitud a, b y c.
La media geométrica es una de las tres "medias pitagóricas", junto con la media aritmética y la media armónica. Para números positivos, la media armónica es la más pequeña, la media aritmética es la más grande, y la media geométrica siempre está en el medio.
Propiedades de la Media Geométrica
- Si tomas el logaritmo de la media geométrica, obtendrás la media aritmética de los logaritmos de los números originales.
- La media geométrica de números positivos siempre es igual o menor que su media aritmética. Solo son iguales si todos los números son idénticos.
Ventajas
- Toma en cuenta todos los números del grupo.
- Es menos afectada por números muy grandes o muy pequeños (valores extremos) que la media aritmética.
Desventajas
- Es un poco más difícil de entender que la media aritmética.
- Su cálculo es más complejo.
- Si uno de los números es 0, la media geométrica siempre será 0. Si hay números negativos, el cálculo puede ser complicado o imposible en los números reales.
La media geométrica es importante cuando varias cantidades se multiplican para obtener un resultado final.
Media Geométrica Ponderada
Así como la media aritmética puede tener "pesos" para darle más importancia a ciertos números, la media geométrica también puede tenerlos. Estos pesos se usan como exponentes en la fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \bar{x} = \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}}
Aquí, las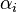 
son los "pesos" que se le dan a cada número.
Ejemplo Práctico: Crecimiento de Ingresos
Imagina una empresa que aumentó sus ingresos un 21% el año pasado y espera aumentarlos un 28% este año. ¿Cuál es el promedio anual de aumento porcentual?
No es simplemente (21% + 28%) / 2 = 24.5%. Si los ingresos iniciales fueran 100, después de dos años serían 100 * (1 + 0.21) * (1 + 0.28) = 100 * 1.21 * 1.28 = 154.88.
Para encontrar el promedio anual de aumento (i), usamos la media geométrica: 100 * (1 + i)2 = 154.88 (1 + i)2 = 1.5488 1 + i = Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{1.5488} = 1.244507 i = 0.244507 = 24.451%
Este es el valor de la media geométrica de 1.21 y 1.28, que es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{(1.21 \cdot 1.28)} .
¿Dónde más aparece la Media Geométrica?
En Geometría
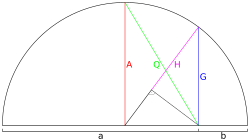
- En un triángulo rectángulo:
* La altura desde el ángulo recto a la hipotenusa es la media geométrica de las dos partes en que divide la hipotenusa. * Un cateto es la media geométrica de la hipotenusa completa y la parte de la hipotenusa que está justo debajo de ese cateto.
- El lado de un cuadrado que tiene la misma área que un rectángulo es la media geométrica de los lados del rectángulo.
- El radio de un círculo que tiene la misma área que una elipse es la media geométrica de los semiejes de la elipse.
En Pesas
Si tienes una sustancia y la pesas con dos balanzas diferentes que dan resultados u y v, el peso más preciso w puede ser la media geométrica de u y v, es decir,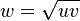 
.
Véase también
En inglés: Geometric mean Facts for Kids
- Media
- Media aritmética
- Media armónica
- Media ponderada
