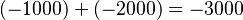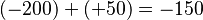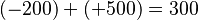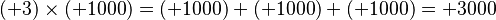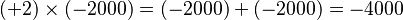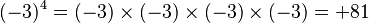robot de la enciclopedia para niños

Número negativo para niños

Enciclopedia para niños

Un número negativo es un tipo de número que tiene un valor menor que cero. Piensa en ellos como lo opuesto a los números positivos, como 7 o 2.5. Los números negativos se usan para representar cosas como pérdidas, deudas, o temperaturas muy frías.

Se escriben con un signo de resta «−» delante, por ejemplo: −4, −2.5, o −√8. Se leen como "menos cuatro" o "cuatro negativo". A veces, a los números positivos se les pone un signo de suma «+» para que se distingan mejor, como +3. Si un número no tiene signo, se entiende que es positivo.

Por ejemplo, si alguien gana 20.000 pesos pero gasta 25.000, al final ha perdido 5.000 pesos. Esto se puede expresar como un cambio de −5.000 pesos en sus ahorros.

Los números negativos también se usan para medir temperaturas. Cuando la temperatura es de 0 °C, el agua se congela. Si hace más frío, la temperatura baja de cero, por ejemplo, a −10 °C. El mercurio, un metal líquido, se congela a unos −39 °C.

¿Para qué sirven los números negativos?

Los números negativos son muy útiles en matemáticas y en la vida diaria. Nos permiten hacer cálculos que antes no eran posibles, como restar un número más grande de uno más pequeño.

Ejemplo: Imagina que juegas a un juego. Si el primer día ganas 50 puntos y al día siguiente pierdes 200 puntos, en total has perdido 150 puntos. Esto se puede escribir como 50 − 200 = −150 puntos. Así, una pérdida se puede ver como una "ganancia negativa".

Números con signo: Positivos, Negativos y Cero

Los números que usamos para contar, como 1, 2, 3, se llaman números naturales. Si les ponemos un signo "menos" «−» delante, se convierten en números enteros negativos, como −1, −2, −3.

Todos los números positivos (como los que tienen decimales o fracciones) también tienen su versión negativa si les ponemos el signo «−». Para diferenciarlos, a veces a los positivos se les pone un signo «+», como +5 o +2/3. Si un número no tiene signo, se asume que es positivo.

El cero es especial: no es ni positivo ni negativo. Se puede escribir con un signo «+» o «−», pero no cambia nada, así que normalmente se deja sin signo.

La recta numérica: ¿Cómo se ordenan los números?

Los números negativos son más pequeños que todos los números positivos y también que el cero. Para entender cómo se ordenan, usamos la recta numérica:

Integers-line.svg

En la recta numérica, los números negativos están a la izquierda del cero. Cuanto más a la izquierda estén, más pequeños son.

Para comparar números negativos, usamos el concepto de valor absoluto.

El valor absoluto de un número es el número sin su signo, siempre positivo. Se representa con dos barras verticales, por ejemplo,


−5

Ahora podemos entender cómo se ordenan los números:

Para comparar dos números diferentes con signo:

  • Si tienen signos distintos, el número con el signo «−» es siempre menor que el que tiene el signo «+».
  • Si tienen el mismo signo:
    • Si el signo es «+», el número con el valor absoluto más pequeño es el menor. Por ejemplo, +1 es menor que +3.
    • Si el signo es «−», el número con el valor absoluto más grande es el menor. Por ejemplo, −5 es menor que −2.

El cero es menor que los números positivos y mayor que los números negativos.

Ejemplo.

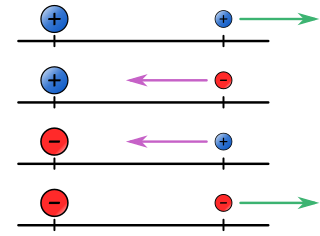
  1. Para comparar +4 y −5: Tienen signos diferentes, así que −5 es menor que +4.
  2. Para comparar +3 y +1: Tienen el mismo signo (+). El que tiene el valor absoluto más pequeño es el menor: +1 es menor que +3.
  3. Para comparar −2 y −5: Tienen el mismo signo (−). El que tiene el valor absoluto más grande es el menor: −5 es menor que −2.

Operaciones con números negativos

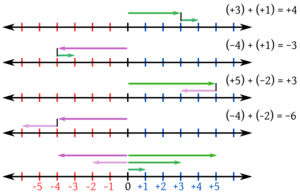
Podemos sumar, restar, multiplicar y dividir números con signo. También podemos calcular potencias. Para no confundirnos, es bueno usar paréntesis, por ejemplo, para sumar −4 y +3, escribimos `(-4) + (+3)`.

Suma de números con signo

Archivo:AdditionIntegers
La suma de dos números con signo puede verse como movimientos en la recta numérica.
Archivo:AdditionRules-2
El valor absoluto y el signo de un número se representan por el tamaño del círculo y su color.

Sumar números negativos es parecido a sumar positivos. Si debes 1000 pesos a un banco y 2000 pesos a otro, en total debes 3000 pesos. Esto se escribe:

(-1000)+(-2000)=-3000

Para sumar números con signos diferentes, piensa en una deuda y una ganancia. Si debes 200 euros y recibes 50 euros, tu deuda se reduce a 150 euros. Si recibes 500 euros, pagas la deuda y te sobran 300 euros.

(-200)+(+50)=-150
(-200)+(+500)=300

Para sumar números con signo, sigue estos pasos:

Para sumar dos números con signo:

  • Si tienen el mismo signo: El resultado tendrá ese mismo signo. Su valor absoluto será la suma de los valores absolutos de los números.
  • Si tienen signos diferentes:
    • El signo del resultado será el signo del número con el valor absoluto más grande.
    • El valor absoluto del resultado será la resta del valor absoluto más grande menos el más pequeño.

Ejemplo.

  1. (+4.5) + (−2.3): Signos diferentes. +4.5 tiene mayor valor absoluto. El signo es «+». Restamos 4.5 − 2.3 = 2.2. Resultado: +2.2.
  2. (+1) + (+5): Mismo signo (+). El signo es «+». Sumamos 1 + 5 = 6. Resultado: +6.
  3. (−6) + (+3/4): Signos diferentes. −6 tiene mayor valor absoluto. El signo es «−». Restamos 6 − 3/4 = 21/4. Resultado: −21/4.
  4. (−4) + (−7): Mismo signo (−). El signo es «−». Sumamos 4 + 7 = 11. Resultado: −11.

Resta de números con signo

Restar números con signo es fácil si lo convertimos en una suma.

Para restar dos números con signo (minuendo menos sustraendo), se suma el minuendo con el sustraendo, pero cambiándole el signo.

Ejemplo.

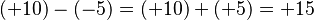
  1. (+10)-(-5)=(+10)+(+5)=+15
  2. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (-7.4)-(+6)=(-7.4)+(-6)=-13.4
  3. (-4) - (-8) = (-4) + (+8) = +4

Multiplicación de números con signo

Archivo:SignsRuleCoulomb
Regla de los signos. La fuerza entre dos cargas eléctricas depende del producto de sus signos.

Multiplicar un número positivo por otro es como repetir una suma:

(+3)\times(+1000) = (+1000) + (+1000) + (+1000) = +3000
(+2)\times(-2000) = (-2000) + (-2000) = -4000

Esto significa que el triple de una ganancia de 1000 pesos es una ganancia de 3000 pesos. Y el doble de una deuda de 2000 pesos es una deuda de 4000 pesos.

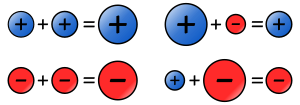
Para multiplicar números con signo, se usa la regla de los signos:

En la multiplicación de dos números con signo:

  • El valor absoluto del resultado es el producto de los valores absolutos de los números.
  • El signo del resultado es «+» si los signos de los números son iguales, y «−» si son diferentes.

Regla de los signos para multiplicar

  • (+) × (+)=(+) Más por más es más.
  • (+) × (−)=(−) Más por menos es menos.
  • (−) × (+)=(−) Menos por más es menos.
  • (−) × (−)=(+) Menos por menos es más.

Ejemplo.

  1. (+4.5) × (−6): Signos diferentes, el resultado es «−». Multiplicamos 4.5 × 6 = 27. Resultado: −27.
  2. (+5) × (+3): Mismo signo, el resultado es «+». Multiplicamos 5 × 3 = 15. Resultado: +15.
  3. (−9) × (−2): Mismo signo, el resultado es «+». Multiplicamos 9 × 2 = 18. Resultado: +18.

División de números con signo

La división de números con signo sigue las mismas reglas que la multiplicación.

En la división de dos números con signo (dividendo entre divisor):

  • El valor absoluto del resultado es la división de los valores absolutos del dividendo y el divisor.
  • El signo del resultado se determina con la regla de los signos: «+» si los signos son iguales y «−» si son diferentes.

Ejemplo.

  1. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (-36) \div 5 = -(36 \div 5) = -7.2
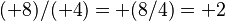
  2. (+8) / (+4) = +(8/4) = +2
  3. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (-31.2) \div (-5.2) = +(31.2 \div 5.2) = +6

Potencias con números negativos

Una potencia es multiplicar un número por sí mismo varias veces.

(-3)^4 = (-3) \times (-3) \times (-3) \times (-3) = +81

Cuando la base es un número negativo:

  • Si el exponente es un número entero par (como 2, 4, 6...), el resultado siempre será positivo.
  • Si el exponente es un número entero impar (como 1, 3, 5...), el resultado siempre será negativo.

Ejemplo.

  1. (+4)+(1/3): La base es positiva, el resultado es «+». El valor absoluto es 41/3. Resultado: +1.587...
  2. (−5)+(2/7): La base es negativa, el exponente es una fracción con denominador impar y numerador par. El signo es «+». El valor absoluto es 52/7. Resultado: +1.583...
  3. (+6)−3: La base es positiva, el resultado es «+». El valor absoluto es 1/(63). Resultado: +1/216.
  4. (−9)+(1/6): La base es negativa y el exponente es una fracción con denominador par. Esta potencia no existe en los números reales.
  5. (−2.3)−10/2: La base es negativa y el exponente es un número entero impar (se simplifica a −5). El signo es «−». El valor absoluto es 1/(2.35). Resultado: −0.0155...

Galería de imágenes

  • 20050501 1315 2558-Bimetall-Zeigerthermometer

    Temperaturas negativas, 'Termómetro marcando una temperatura positiva'. Si la temperatura a la que el agua se congela es 0 °C, las temperaturas más bajas se representan con números negativos y las más altas con positivos.

Véase también

Kids robot.svg En inglés: Negative number Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Número_negativo&oldid=5043106»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Número negativo para Niños. Enciclopedia Kiddle.