Geometría algebraica para niños

La geometría algebraica es una rama de las matemáticas que une dos grandes áreas: el álgebra abstracta (que estudia las reglas de las operaciones matemáticas) y la geometría analítica (que usa coordenadas para describir formas). Imagina que es como un puente que conecta el mundo de las ecuaciones con el mundo de las formas y figuras.

Esta área de las matemáticas se enfoca en estudiar los conjuntos de soluciones de sistemas de ecuaciones algebraicas. Cuando tienes una ecuación con varias variables (como 'x', 'y', 'z'), las soluciones no son solo números, sino que forman figuras geométricas. La geometría algebraica busca entender estas figuras, sus propiedades y cómo se relacionan entre sí. No solo se trata de encontrar una solución, sino de comprender todas las soluciones posibles y la forma que crean.

Los objetos principales que estudia la geometría algebraica son las variedades algebraicas. Estas son las formas geométricas que aparecen cuando resuelves sistemas de ecuaciones que usan polinomios (expresiones como x² + 3y - 5). Algunos ejemplos de estas formas son las líneas rectas, circunferencias, parábolas, elipses, hipérbolas, y curvas más complejas como las curvas elípticas. En estas curvas algebraicas planas, un punto pertenece a la curva si sus coordenadas (sus valores de 'x' y 'y') hacen que la ecuación sea verdadera.

La geometría algebraica es muy importante en las matemáticas modernas. Se conecta con otras áreas como el análisis complejo (que estudia funciones con números especiales), la topología (que estudia las propiedades de las formas que no cambian al estirarlas o doblarlas) y la teoría de números (que estudia las propiedades de los números).

Historia de la geometría algebraica

La idea de usar coordenadas para ubicar puntos en un plano o espacio, desarrollada por Descartes, es fundamental para la geometría algebraica. Un punto en una variedad algebraica es simplemente un conjunto de coordenadas que satisface las ecuaciones que definen esa forma.

Sin embargo, la forma en que entendemos las coordenadas ha cambiado mucho desde el siglo XIX. Al principio, se pensaba que las coordenadas solo podían ser números reales. Pero luego se aceptaron los números complejos (que incluyen la raíz cuadrada de números negativos), y después, elementos de cualquier campo (un conjunto de números donde se pueden hacer sumas, restas, multiplicaciones y divisiones). Las coordenadas homogéneas de la geometría proyectiva también ampliaron la idea de cómo se pueden describir los puntos, haciendo la geometría algebraica aún más rica.

Ramas de la geometría algebraica en el siglo XX

En el siglo XX, la geometría algebraica se dividió en varias áreas de estudio:

• La rama principal se enfoca en estudiar los puntos de las variedades algebraicas usando números complejos o números de un cuerpo algebraicamente cerrado (un tipo especial de campo donde todas las ecuaciones polinómicas tienen solución).
• La geometría algebraica real estudia los puntos de una variedad algebraica que son números reales.
• La geometría diofántica y la geometría aritmética estudian los puntos de una variedad algebraica usando coordenadas de campos que no son algebraicamente cerrados, como los números racionales (fracciones) o los campos finitos (conjuntos de números con una cantidad limitada de elementos).
• Una parte importante de la teoría de la singularidad se dedica a estudiar los puntos "especiales" o "extraños" de las variedades algebraicas, donde la forma no es suave.
• La geometría algebraica computacional es un área más reciente que combina la geometría algebraica con la álgebra computacional. Utiliza algoritmos y software de computadora para estudiar las propiedades de las variedades algebraicas de forma práctica.

Gran parte del desarrollo moderno de la geometría algebraica se ha centrado en las propiedades "intrínsecas" de las variedades, es decir, aquellas que no dependen de cómo se dibujan o se colocan en un espacio. Esto es similar a lo que ocurre en otras áreas de la geometría. Un gran avance en esta dirección fue la teoría de esquemas de Alexander Grothendieck. Esta teoría permite estudiar las variedades algebraicas de una manera más general, extendiendo la idea de lo que es un "punto". Por ejemplo, la prueba de Andrew Wiles del último teorema de Fermat es un ejemplo de lo poderosa que es esta forma de pensar.

Ceros de polinomios simultáneos

En la geometría algebraica clásica, el interés principal son los conjuntos de puntos donde una o más ecuaciones polinómicas se hacen cero al mismo tiempo. Esto significa que estos puntos satisfacen todas las ecuaciones a la vez.

Por ejemplo, una esfera de radio r en el espacio tridimensional se puede definir como el conjunto de todos los puntos (x, y, z) que cumplen la ecuación:

Imagina un círculo "inclinado" en el espacio tridimensional. Este se puede definir como el conjunto de todos los puntos (x, y, z) que satisfacen dos ecuaciones polinómicas al mismo tiempo:

Variedades afines

Para entender mejor, empezamos con un cuerpo k. En la geometría algebraica clásica, este cuerpo era siempre C (los números complejos), pero muchos resultados también funcionan si k es un cuerpo algebraicamente cerrado. Definimos 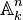, llamado el n-espacio afín sobre k, como kⁿ. Esto es, simplemente, un conjunto de puntos donde cada punto tiene 'n' coordenadas que pertenecen al cuerpo 'k'.

Una función 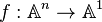se llama regular si se puede escribir como un polinomio. Es decir, si existe un polinomio p tal que para cualquier punto (t₁,...,t_n) en 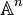, el valor de la función es f(t₁,...,t_n)=p(t₁,...,t_n).

Decimos que un polinomio se anula en un punto si, al reemplazar las variables del polinomio con las coordenadas del punto, el resultado es cero. Si tenemos un conjunto de polinomios S, el conjunto anulador de S (o locus anulador), que se escribe V(S), es el conjunto de todos los puntos donde cada polinomio de S se anula.

Un subconjunto de 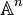que es un V(S) para algún S se llama conjunto algebraico afín. La letra V viene de "variedad". A veces, un V(S) se llama variedad algebraica afín si no se puede dividir en dos conjuntos algebraicos afines más pequeños.

Si tenemos un conjunto V que sabemos que es una variedad, nos gustaría saber qué polinomios lo definen. Definimos I(V) como el conjunto de todos los polinomios cuyo conjunto anulador contiene a V. I(V) siempre es un Ideal (un tipo especial de conjunto de polinomios).

Funciones regulares

Así como las funciones continuas son importantes en los espacios topológicos, y las funciones suaves en las variedades diferenciables, en la geometría algebraica hay una clase natural de funciones llamadas regulares. Una función regular sobre un conjunto algebraico V (que está dentro de 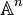) es una función que se obtiene al "restringir" una función regular de 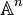a solo los puntos de V.

Las funciones regulares en V también forman un anillo (una estructura matemática donde se pueden sumar y multiplicar elementos), que se llama el anillo coordenado de V. Este anillo se puede entender como el resultado de dividir el anillo de funciones regulares de 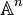por el ideal I(V).

El espacio proyectivo

Imagina la variedad V(y=x²), que es una parábola. Si la dibujas, verás que a medida que 'x' se hace muy grande o muy pequeña, la curva se extiende hacia el infinito. Ahora compara esto con V(y=x³), que es una ecuación cúbica. Su comportamiento "al infinito" es diferente. Sin embargo, es difícil describir este comportamiento si solo nos quedamos en el espacio afín.

Para solucionar esto, los matemáticos usan el espacio proyectivo. Este espacio es como el espacio afín, pero le añade "puntos en el infinito". Estos puntos extra nos ayudan a entender mejor el comportamiento de las variedades cuando se extienden indefinidamente. Por ejemplo, la curva V(y=x³) tiene un punto "singular" (un punto donde la curva no es suave) en uno de esos puntos extra, mientras que V(y=x²) es suave incluso en el infinito.

Los primeros geómetras algebraicos se dieron cuenta de que el espacio proyectivo tiene propiedades mucho mejores que el espacio afín. Por ejemplo, el Teorema de Bézout, que habla sobre cuántos puntos de intersección tienen dos variedades, se entiende mejor en el espacio proyectivo. Por eso, el espacio proyectivo es muy importante en la geometría algebraica.

El punto de vista moderno

El estudio moderno de la geometría algebraica ha cambiado la forma en que se ven sus objetos básicos. Las variedades ahora se entienden dentro de un concepto más amplio llamado esquema, desarrollado por Alexander Grothendieck. Esta idea surgió al pensar que si ciertas estructuras algebraicas (las k-álgebras reducidas finitamente generadas) eran objetos geométricos, quizás cualquier anillo conmutativo (un tipo de estructura algebraica) también podría serlo. Esta nueva perspectiva ha sido muy útil y es la base de la investigación actual en geometría algebraica.

Esta superficie de Togliatti es una superficie algebraica de quinto grado. La imagen representa una porción de su lugar geométrico real

Véase también

En inglés: Algebraic geometry Facts for Kids