Descomposición en fracciones simples para niños

Enciclopedia para niños

El método de descomposición en fracciones simples es una técnica matemática que nos ayuda a simplificar fracciones que tienen polinomios (expresiones con letras y números) tanto arriba (numerador) como abajo (denominador). Imagina que tienes una fracción complicada y quieres convertirla en una suma de fracciones más sencillas. Este método es muy útil para resolver problemas más avanzados en matemáticas.

Para poder usar este método, es muy importante que el grado (el exponente más alto de la letra) del polinomio de abajo (el denominador) sea mayor que el grado del polinomio de arriba (el numerador).

Contenido

¿Cómo funciona la descomposición en fracciones simples?
- Tipos de factores en el denominador
¿Cómo encontramos los números que faltan?
Véase también

¿Cómo funciona la descomposición en fracciones simples?

Para que este método funcione, la parte de abajo de la fracción (el denominador) debe poder escribirse como una multiplicación de expresiones más sencillas. Estas expresiones pueden ser de dos tipos:

Factores lineales: Son expresiones como (x + un número) o (un número * x + otro número).
Factores cuadráticos: Son expresiones como (un número * x² + otro número * x + un tercer número) que no se pueden simplificar más.

Una vez que el denominador está factorizado, la fracción original se puede escribir como una suma de fracciones más simples. Cada una de estas fracciones nuevas tendrá uno de los factores del denominador original.

Tipos de factores en el denominador

Existen diferentes situaciones, dependiendo de cómo sean los factores del denominador:

Factores lineales diferentes

Esto ocurre cuando el denominador se puede escribir como una multiplicación de expresiones lineales que no se repiten. Por ejemplo, si el denominador es (x+1)(x+2).

Factores lineales repetidos

Aquí, el denominador tiene expresiones lineales que se repiten. Por ejemplo, si el denominador es (x+1)(x+1) o (x+1)³.

Factores cuadráticos diferentes

En este caso, el denominador tiene expresiones cuadráticas que no se pueden simplificar más y que son distintas entre sí. Por ejemplo, (x²+1)(x²+2).

Factores cuadráticos repetidos

Similar al caso anterior, pero las expresiones cuadráticas se repiten. Por ejemplo, (x²+1)(x²+1) o (x²+1)².

¿Cómo encontramos los números que faltan?

Cuando descomponemos una fracción, aparecen unas letras (como A, B, C) que representan números que necesitamos encontrar. A estos números se les llama "constantes".

Para hallar estas constantes, podemos seguir estos pasos:

Primero, igualamos la fracción original a la suma de las fracciones simples con las constantes desconocidas.
Luego, multiplicamos toda la ecuación por el denominador original para eliminar las fracciones.
Después, podemos asignar valores a la letra 'x' que hagan que algunas partes de la ecuación se vuelvan cero, lo que nos ayuda a encontrar las constantes más fácilmente.
Si no es posible hacer que se vuelvan cero, podemos desarrollar la expresión y comparar los coeficientes (los números que acompañan a las letras) de ambos lados de la ecuación. Esto nos dará un sistema de ecuaciones que podemos resolver para encontrar los valores de las constantes.

Ejemplo 1: Factores lineales diferentes

Imagina que queremos descomponer la fracción: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x+3}{(x+1)(x+2)}

Podemos escribirla como una suma de dos fracciones más simples: 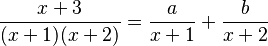$\frac{x+3}{(x+1)(x+2)}=\frac{a}{x+1}+\frac{b}{x+2}$

Nuestro objetivo es encontrar los valores de 'a' y 'b'.

1. Multiplicamos toda la ecuación por Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x+1)(x+2) para quitar los denominadores: 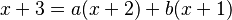$x+3= a (x+2)+ b (x+1)$

2. Ahora, elegimos valores para 'x' que nos ayuden a encontrar 'a' y 'b'. * Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = -2 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -2+3 = a (-2+2)+b(-2+1) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a(0) + b(-1) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = -b Así que, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b = -1 .

* Si $x = -1$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -1+3 = a (-1+2)+b(-1+1) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 = a(1) + b(0) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 = a Así que, $a = 2$ .

3. ¡Listo! Hemos encontrado los valores. La fracción descompuesta es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x+3}{(x+1)(x+2)}=\frac{2}{x+1}+\frac{-1}{x+2}

Ejemplo 2: Factores lineales repetidos

Vamos a descomponer la fracción: 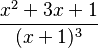$\frac{x^2+3x+1}{(x+1)^3}$

Como el factor Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x+1) se repite tres veces, la descomposición será: 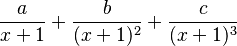$\frac{a}{x+1}+\frac{b}{(x+1)^2}+\frac{c}{(x+1)^3}$

1. Multiplicamos por 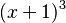$(x+1)^3$ para eliminar los denominadores: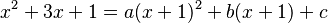 $x^2+3x+1=a(x+1)^2+b(x+1)+c$

2. Asignamos valores a 'x' para encontrar 'a', 'b' y 'c'. * Si $x = -1$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (-1)^2+3(-1)+1 = a(-1+1)^2+b(-1+1)+c Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1-3+1 = a(0)+b(0)+c Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -1 = c Así que, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c = -1 .

* Si 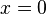$x = 0$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (0)^2+3(0)+1 = a(0+1)^2+b(0+1)+c Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a(1)^2+b(1)+c Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a+b+c Como ya sabemos que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c = -1 , sustituimos: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a+b-1 , lo que nos da Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a+b = 2 .

* Si $x = 1$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (1)^2+3(1)+1 = a(1+1)^2+b(1+1)+c Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1+3+1 = a(2)^2+b(2)+c Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5 = 4a+2b+c Sustituimos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c = -1 : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5 = 4a+2b-1 , lo que nos da Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4a+2b = 6 .

3. Ahora tenemos un sistema de dos ecuaciones con 'a' y 'b': * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a+b = 2 * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4a+2b = 6

Podemos resolverlo. Por ejemplo, de la primera ecuación, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b = 2-a . Sustituimos en la segunda: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4a+2(2-a) = 6 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4a+4-2a = 6 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2a+4 = 6 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2a = 2 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a = 1

Ahora, encontramos 'b': Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b = 2-a = 2-1 = 1 .

4. Finalmente, la descomposición es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{x^2+3x+1}{(x+1)^3} = \frac{1}{x+1}+\frac{1}{(x+1)^2}+\frac{-1}{(x+1)^3}

Ejemplo 3: Factores cuadráticos diferentes

Consideremos la fracción: 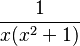$\frac{1}{x(x^2+1)}$

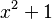Aquí tenemos un factor lineal ( $x$ ) y un factor cuadrático ( $x^2+1$ ) que no se puede simplificar más. La descomposición será: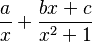 $\frac{a}{x}+\frac{bx+c}{x^2+1}$

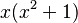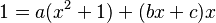
1. Multiplicamos por $x(x^2+1)$ : $1=a(x^2+1)+(bx+c)x$

2. Asignamos valores a 'x': * Si 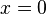$x = 0$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a(0^2+1)+(b(0)+c)(0) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a(1)+0 Así que, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a = 1 .

* Si $x = 1$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a(1^2+1)+(b(1)+c)(1) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a(2)+b+c Como $a=1$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = 2(1)+b+c , lo que nos da Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -1 = b+c .

* Si $x = -1$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a((-1)^2+1)+(b(-1)+c)(-1) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = a(1+1)+(-b+c)(-1) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = 2a+b-c Como $a=1$ : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 = 2(1)+b-c , lo que nos da Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -1 = b-c .

3. Tenemos un sistema de dos ecuaciones para 'b' y 'c': * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b+c = -1 * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b-c = -1

Si sumamos ambas ecuaciones: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (b+c) + (b-c) = -1 + (-1) Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2b = -2 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b = -1

Ahora, sustituimos 'b' en la primera ecuación: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): -1+c = -1 $c = 0$

4. Finalmente, la descomposición es: 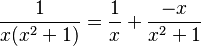$\frac{1}{x(x^2+1)}=\frac{1}{x}+\frac{-x}{x^2+1}$

Véase también

En inglés: Partial fraction decomposition Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Descomposición_en_fracciones_simples&oldid=4692872»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Descomposición en fracciones simples para Niños. Enciclopedia Kiddle.