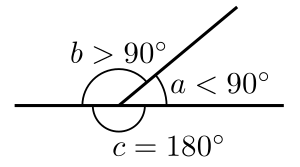Geometría para niños

La geometría es una rama de las matemáticas que estudia las formas, tamaños y posiciones de las figuras en el plano y en el espacio. Se ocupa de elementos como puntos, rectas, planos, polígonos, poliedros, curvas y superficies.

La geometría es muy útil en muchas áreas. Es la base del dibujo técnico y ayuda a entender cómo funcionan instrumentos como el compás y el sistema de posicionamiento global (GPS). Sus ideas se usan en física aplicada, arquitectura, geografía, cartografía, astronomía, navegación y hasta en la creación de artesanía.

Historia de la Geometría

Esta sección es un extracto de Historia de la geometría.

La Geometría como una de las Artes Liberales y Euclides.

La geometría es una de las ciencias más antiguas que existen. Al principio, era un conjunto de conocimientos prácticos para medir longitudes, áreas y volúmenes.

La civilización babilónica fue una de las primeras en estudiar geometría. La invención de la rueda les ayudó a entender la circunferencia y a descubrir el número π (pi). También crearon un sistema para medir el tiempo y calcular el área de figuras como el trapecio.

En el antiguo Egipto, la geometría estaba muy avanzada. Euclides, un matemático griego del siglo III a. C., organizó la geometría de una forma lógica y sistemática. Sus ideas, conocidas como geometría euclidiana, se describen en su famoso libro Los Elementos, que fue una guía por muchos siglos.

El estudio de las estrellas y los planetas en la astronomía y la cartografía (hacer mapas) también impulsó la geometría por más de mil años. Más tarde, René Descartes unió el álgebra con la geometría, creando la geometría analítica. Esto permitió representar figuras geométricas con ecuaciones. Matemáticos como Leonhard Euler y Carl Friedrich Gauss exploraron más a fondo las formas, lo que llevó al desarrollo de la topología y la geometría diferencial.

Conceptos Fundamentales de la Geometría

Un teorema descubierto y probado por Arquímedes: una esfera tiene ²⁄₃ del volumen de su cilindro circunscrito

La geometría busca ir más allá de lo que vemos a simple vista. Para ello, usa un método muy preciso llamado sistema axiomático. El primer sistema así lo creó Euclides. Más tarde, a principios del siglo XX, David Hilbert propuso otro sistema más completo.

En estos sistemas, los conceptos como "punto", "recta" y "plano" se vuelven ideas abstractas. Esto significa que cualquier grupo de objetos que cumpla con las definiciones y reglas básicas (axiomas) también cumplirá con todos los teoremas de esa geometría.

A continuación, veremos algunos de los conceptos más importantes en geometría.

Axiomas y Postulados: Las Reglas del Juego

La geometría esférica es un ejemplo de geometría no euclidiana.

En la geometría euclidiana, los axiomas y postulados son afirmaciones que relacionan conceptos como el punto, la recta y el plano. Euclides propuso cinco postulados. El quinto, el postulado de las paralelas, fue muy debatido y llevó al descubrimiento de nuevas geometrías, como la elíptica (de Bernhard Riemann) y la hiperbólica (de Nikolái Lobachevski).

En la geometría analítica, los axiomas se definen usando ecuaciones y se basan en el análisis matemático y el álgebra. Aquí, un punto, una recta o un plano pueden ser representados por una función matemática.

Ilustración del postulado de las paralelas de Euclides.

Euclides usó un enfoque abstracto en su libro Elementos. Introdujo axiomas o postulados que describen propiedades básicas de puntos, líneas y planos. A partir de ellos, dedujo otras propiedades de forma lógica. Este método riguroso se conoce como geometría axiomática. En el siglo XIX, el descubrimiento de las geometrías no euclidianas por matemáticos como Nikolai Ivanovich Lobachevsky, János Bolyai y Carl Friedrich Gauss renovó el interés en esta área. En el siglo XX, David Hilbert usó el razonamiento axiomático para dar una base moderna a la geometría.

Puntos: Los Ladrillos Básicos

Los puntos son considerados los elementos más básicos en la geometría euclidiana. Euclides los definió como "aquello que no tiene parte". En muchas áreas de la geometría, como la geometría analítica y la topología, se considera que todos los objetos están formados por puntos.

Líneas: Caminos Rectos o Curvos

Euclides describió una línea como "longitud sin ancho". En las matemáticas modernas, el concepto de línea depende de cómo se defina la geometría. Por ejemplo, en geometría analítica, una línea en el plano es el conjunto de puntos cuyas coordenadas cumplen una ecuación lineal. En espacios curvos, una línea se generaliza a una "geodésica".

Planos: Superficies Infinitas

Un plano es una superficie plana que se extiende infinitamente en dos dimensiones. Los planos se usan en todas las áreas de la geometría. Se pueden estudiar sin considerar distancias o ángulos, o como un espacio donde se analizan las relaciones entre puntos y líneas.

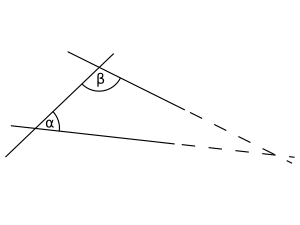
Ángulos: La Inclinación entre Líneas

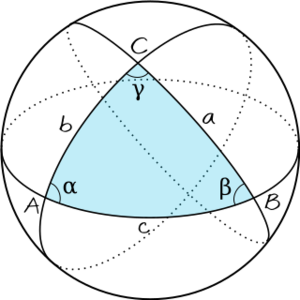
Euclides definió un ángulo plano como la inclinación entre dos líneas que se encuentran en un plano y no son rectas entre sí. Hoy en día, un ángulo es la figura formada por dos "rayos" (lados del ángulo) que comparten un punto final común, llamado vértice.

Ángulos agudos (a), obtusos (b) y rectos (c). Los ángulos agudos y obtusos también se denominan ángulos oblicuos.

En la geometría euclidiana, los ángulos se usan para estudiar polígonos y triángulos. El estudio de los ángulos en un triángulo o en un círculo es la base de la trigonometría.

Curvas: Formas que se Doblan

Una curva es un objeto de una dimensión que puede ser recto (como una línea) o no. Las curvas en un espacio de dos dimensiones se llaman curvas planas, y las de tres dimensiones, curvas espaciales.

En topología, una curva se define mediante una función matemática. En la geometría diferencial, se usa una definición similar, pero se requiere que la función sea "diferenciable". La geometría algebraica estudia las curvas algebraicas, que se definen con ecuaciones polinómicas.

Superficies: Formas Bidimensionales

Una esfera es una superficie que se puede definir paramétricamente (como x Plantilla:= r sin θ cos φ, y Plantilla:= r sin θ sin φ, z Plantilla:= r cos θ) o en forma implícita (como x² + y² + z² − r² Plantilla:= 0.)

Una superficie es un objeto de dos dimensiones, como una esfera o un paraboloide. En geometría diferencial y topología, las superficies se describen como "parches" bidimensionales que se unen. En geometría algebraica, se describen con ecuaciones polinómicas.

Variedades: Generalizando Formas

Una variedad es una idea más general que las curvas y superficies. En topología, una variedad es un espacio donde cada punto se parece a un espacio euclidiano. Las variedades se usan mucho en física, por ejemplo, en la relatividad general.

Longitud, Área y Volumen: Midiendo el Tamaño

La longitud, el área y el volumen describen el tamaño o la extensión de un objeto en una, dos y tres dimensiones, respectivamente.

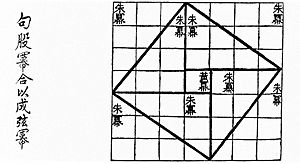
En la geometría euclidiana, la longitud de un segmento de línea se puede calcular con el teorema de Pitágoras.

El área y el volumen pueden definirse como cantidades básicas o calcularse a partir de las longitudes. Los matemáticos han encontrado muchas fórmulas para el área y el volumen de diferentes objetos. En el cálculo, el área y el volumen se pueden definir usando integrales.

Métricas y Medidas: Distancias y Tamaños

Comprobación visual del teorema de Pitágoras para el triángulo (3, 4, 5) como en el Zhoubi Suanjing 500-200 a. C. El teorema de Pitágoras es una consecuencia de la métrica euclidiana].

El concepto de longitud o distancia se puede generalizar con las "métricas". Por ejemplo, la métrica euclidiana mide la distancia en el plano euclidiano, mientras que la métrica hiperbólica mide la distancia en el plano hiperbólico.

Además, los conceptos de longitud, área y volumen se amplían con la teoría de la medida, que estudia cómo asignar un tamaño o "medida" a conjuntos, siguiendo reglas similares a las del área y volumen clásicos.

Congruencia y Similitud: Formas Iguales o Parecidas

La congruencia y la similitud describen cuándo dos formas tienen características parecidas. En la geometría euclidiana, la similitud se usa para objetos que tienen la misma forma, mientras que la congruencia se usa para objetos que son iguales en tamaño y forma.

Estos conceptos se generalizan en la geometría de transformación, que estudia las propiedades de los objetos geométricos que se mantienen iguales después de diferentes tipos de cambios.

Construcciones con Compás y Regla: Dibujando Formas

Los geómetras clásicos se enfocaron en cómo construir objetos geométricos usando solo un compás y una regla, en un número limitado de pasos. Algunos problemas eran muy difíciles o imposibles de resolver solo con estos instrumentos, lo que llevó a usar otras curvas y dispositivos mecánicos.

Dimensión: Más Allá de lo que Vemos

El copo de nieve de Koch, con dimensión fractal = log4 / log3 y dimensión topológica = 11

Mientras que la geometría tradicional se limitaba a una línea (una dimensión), un plano (dos dimensiones) y nuestro mundo (tres dimensiones), los matemáticos y físicos han usado dimensiones superiores por casi dos siglos. Por ejemplo, la posición de un tornillo se puede describir con cinco coordenadas.

En topología general, el concepto de dimensión se ha extendido a la dimensión infinita y a números reales positivos (en geometría fractal).

Simetría: Belleza y Orden en las Formas

Un mosaico del plano hiperbólico

La simetría en geometría es tan antigua como la propia ciencia. Formas simétricas como el círculo, los polígonos regulares y los sólidos platónicos eran muy importantes para muchos filósofos antiguos. Los patrones simétricos aparecen en la naturaleza y en el arte, como en los dibujos de Leonardo da Vinci y MC Escher.

En el siglo XIX, se estudió intensamente la relación entre simetría y geometría. El Programa de Erlangen de Felix Klein propuso que la simetría, a través de los "grupos de transformación", define lo que es la geometría. En la geometría euclidiana, la simetría se ve en las congruencias (movimientos que no cambian la forma ni el tamaño).

Un tipo diferente de simetría es la dualidad en la geometría proyectiva. Esto significa que en muchos teoremas, si cambias "punto" por "plano", "unir" por "encontrar", etc., el resultado sigue siendo un teorema verdadero.

Topología y Geometría

El nudo de trébol

La topología, que se desarrolló mucho en el siglo XX, es un tipo de geometría transformacional. En topología, las transformaciones que mantienen las propiedades de las figuras son los "homeomorfismos". Esto se suele explicar diciendo que "la topología es la geometría de la página de goma", porque puedes estirar o doblar una figura sin romperla, y sus propiedades topológicas se mantienen.

Tipos de Geometría

Desde los antiguos griegos, ha habido muchas contribuciones a la geometría, especialmente a partir del siglo XVIII. Esto ha llevado a la creación de muchas ramas de la geometría con enfoques muy diferentes. Podemos clasificar los tipos de geometría de varias maneras:

Geometrías según el Espacio

Los antiguos griegos solo conocían la geometría euclídea, que fue organizada por Euclides en sus Elementos. Esta geometría se basaba en cinco postulados básicos. Los primeros cuatro eran muy aceptados, pero el quinto postulado (el de las paralelas) fue cuestionado. Al intentar demostrarlo, se descubrió que existían otras geometrías donde este postulado no se cumplía. Así surgieron diferentes familias de geometrías:

• La geometría absoluta: Se basa solo en los primeros cuatro postulados de Euclides.
• La geometría euclídea: Es la geometría que se obtiene al aceptar también el quinto postulado. Los griegos estudiaron dos variantes:
  • Geometría euclídea del plano
  • Geometría euclídea del espacio
• La geometría clásica: Recopila resultados de las geometrías euclídeas.

A partir del siglo XIX, se concluyó que podían definirse geometrías no euclídeas, como:

• La geometría elíptica
• La geometría esférica
• La geometría finita
• La geometría hiperbólica
• La geometría riemanniana

Geometrías por Transformaciones

En el siglo XIX, Felix Klein desarrolló el Programa de Erlangen, que propuso otra forma de ver la geometría: estudiar qué propiedades de las figuras se mantienen iguales bajo diferentes tipos de transformaciones matemáticas. Esto llevó a identificar grupos de operaciones y a clasificar la geometría según las transformaciones que no cambian las propiedades de los objetos. Algunas de estas ramas son:

• Geometría afín
• Geometría conforme
• Geometría convexa
• Geometría discreta
• Geometría de incidencia
• Geometría ordenada
• Geometría proyectiva

Geometría por Tipo de Representación

Aunque Euclides se centró en conceptos que se podían dibujar (puntos, líneas, círculos), el desarrollo de otras ramas de las matemáticas permitió aplicar sus herramientas a problemas geométricos. Así nacieron:

• La geometría algebraica
• La geometría analítica
• La geometría descriptiva
• La Topología geométrica
• La geometría diferencial, que incluye ramas como:
  • Geometría diferencial discreta
  • La geometría de curvas y superficies
    • La Geometría diferencial de curvas
    • La Geometría diferencial de superficies
  • La Geometría diferencial de hipersuperficies
  • Geometría diferencial de variedades
  • La geometría de Riemann
• La Geometría fractal
• Geometría sintética

Aplicaciones de la Geometría

Además de las ramas teóricas, la geometría tiene muchas aplicaciones prácticas hoy en día, como:

• Geometría computacional
• Geometría constructiva de sólidos
• Geometría molecular

Aprender Geometría

Aprender geometría ayuda a desarrollar habilidades para visualizar y para argumentar de forma lógica.

Es importante que los profesores busquen un equilibrio entre enseñar a visualizar y a argumentar, ya que ambas habilidades son clave. La idea no es solo aprender fórmulas de memoria, sino que los estudiantes aprendan a pensar de manera lógica.

Desde pequeños, los seres humanos creamos ideas sobre el mundo físico que nos rodea. Esto nos impulsa a querer entenderlo. El estudio de la geometría contribuye mucho a desarrollar esas habilidades de visualización espacial. Aunque la geometría es muy antigua, no fue hasta la década de 1950 que los educadores matemáticos se interesaron en cómo la capacidad matemática se relaciona con la capacidad espacial.

Algunas dificultades que los estudiantes pueden tener al estudiar geometría incluyen: resolver problemas con álgebra, calcular perímetros, áreas y volúmenes (porque no saben qué fórmula usar), y entender lo que dice un problema. En los cursos más avanzados, la principal dificultad suele ser interpretar los problemas. En los cursos iniciales, las dificultades pueden ser comprender las fórmulas de perímetro, área y volumen, aprender las definiciones, resolver problemas con álgebra o extraer información de un dibujo geométrico.

Galería de imágenes

• 

  Alegoría de la geometría, de Hans Sebald Beham (s. XVI).

Véase también

En inglés: Geometry Facts for Kids