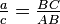Seno (trigonometría) para niños
Datos para niños Seno |
||
|---|---|---|
 Gráfica de Seno
|
||
| Definición | sen (x) | |
| Dominio |  |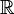
|
| Imagen | [-1,1] | |
| Cálculo infinitesimal | ||
| Derivada | cos x | |
| Función primitiva | -cos x + c | |
| Función inversa | arcsen x | |
En matemática, el seno es una de las seis funciones trigonométricas principales. También se les llama funciones circulares. Es una función que toma cualquier número real como entrada y siempre da un resultado entre -1 y 1.
Se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = \sin (x) . A veces se abrevia como sen en español y sin en inglés.
Contenido
- ¿De dónde viene la palabra "seno"?
- ¿Qué es el seno en un triángulo?
- Relaciones importantes del seno
- Seno de la suma de dos ángulos
- Seno del ángulo doble
- Seno del ángulo mitad
- ¿Cómo se usa el seno en la programación y calculadoras?
- Representación gráfica del seno
- Otros temas relacionados
- Véase también
¿De dónde viene la palabra "seno"?
La palabra "seno" tiene una historia interesante. Un matemático de la India llamado Aryabhata (que vivió hace mucho tiempo, entre los años 476 y 550) estudió un concepto similar. Él lo llamó ardhá-jya, que significaba "media cuerda".
Cuando los científicos árabes tradujeron sus trabajos, usaron la palabra jiba. Como en árabe escrito a menudo se omiten las vocales, se abrevió a jb. Más tarde, algunos traductores pensaron que jb era la abreviatura de jiab, que significa "bahía" o "cavidad".
A finales del siglo XII, un traductor italiano llamado Gerardo de Cremona tradujo estos textos al latín. Él usó la palabra latina sinus, que también significa "hueco", "cavidad" o "bahía". Con el tiempo, esta palabra sinus se convirtió en el "seno" que usamos hoy en español.
¿Qué es el seno en un triángulo?
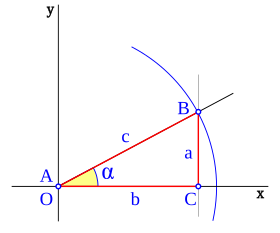
En trigonometría, el seno de un ángulo en un triángulo rectángulo se define de una forma especial. Es la relación entre la longitud del cateto opuesto a ese ángulo y la longitud de la hipotenusa.
Por ejemplo, si tienes un ángulo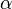 
en un triángulo rectángulo, el seno de 
se calcula así:
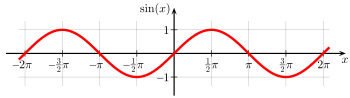
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin \alpha=\frac{\text{cateto opuesto}}{\text{hipotenusa}}
Lo interesante es que esta relación no cambia, no importa qué tan grande o pequeño sea el triángulo, siempre y cuando el ángulo sea el mismo.
Si dibujamos un triángulo dentro de un círculo de radio uno (llamado círculo goniométrico), el valor del seno de un ángulo es simplemente la altura del punto donde el triángulo toca el círculo.
Relaciones importantes del seno
El seno se relaciona con otras funciones trigonométricas de varias maneras. Aquí te mostramos algunas de las más comunes:
- El seno es una función impar. Esto significa que si cambias el signo del ángulo, el signo del seno también cambia:
:Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin \; (-x) = -\sin (x)
- El seno es una función periódica. Esto quiere decir que su gráfica se repite cada cierto intervalo. Para el seno, se repite cada
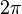(o 360 grados).
:Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin \; \alpha=\;\;\;\sin \; ( \alpha + 2 k \pi ) ,\;\; k \in \mathbb{Z} Donde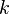 
es cualquier número entero.
Seno y coseno
El coseno es otra función trigonométrica muy relacionada con el seno. La gráfica del coseno es como la del seno, pero un poco desplazada.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin \alpha=\cos\left(\alpha- \frac{\pi}{2}\right)
También, hay una identidad muy famosa que conecta el seno y el coseno:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin^2 \alpha + \cos^2 \alpha = 1
Esto significa que el cuadrado del seno de un ángulo más el cuadrado del coseno del mismo ángulo siempre es igual a 1.
Seno y tangente
La tangente de un ángulo también se puede expresar usando el seno y el coseno.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \tan \alpha = \frac{\sin \alpha}{\cos \alpha}
A partir de esto, podemos encontrar una relación para el seno:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin \alpha = \cfrac {\tan \alpha}{\sqrt{1 + \tan^2\alpha}}
Seno y cosecante
El seno y la cosecante son funciones inversas. Esto significa que si multiplicas el seno de un ángulo por la cosecante del mismo ángulo, el resultado es 1.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin \alpha = \cfrac{1}{\csc \alpha}
Seno de la suma de dos ángulos
Si quieres calcular el seno de la suma de dos ángulos, puedes usar esta fórmula:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin\left(\alpha +\beta\right)=\sin\alpha\cos\beta +\cos\alpha\sin\beta
Seno del ángulo doble
Si tienes un ángulo y quieres saber el seno del doble de ese ángulo, puedes usar esta fórmula:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin\left(2\alpha\right)=2\sin\alpha\cos\alpha
Seno del ángulo mitad
Para encontrar el seno de la mitad de un ángulo, se usa esta fórmula:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \vert \sin \theta \vert=\sqrt{\frac{1-\cos(2\theta)}{2}}
El signo dependerá de en qué parte del círculo se encuentre la mitad del ángulo.
¿Cómo se usa el seno en la programación y calculadoras?
Muchas calculadoras y lenguajes de programación tienen una función para calcular el seno. Es importante saber si tu calculadora está configurada para usar grados sexagesimales o radianes, ya que el resultado será diferente.
Por ejemplo:
- Seno de 45 grados es aproximadamente 0,7071.
- Seno de 45 radianes es aproximadamente 0,8509.
Para cambiar entre grados y radianes, puedes usar estas fórmulas:
- Radianes = Grados *
/180 - Grados = Radianes * 180/
Puedes comprobar el modo de tu calculadora con valores conocidos:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin \pi = 0 si está en modo radianes.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sin 90 = 1 si está en modo grados.
Representación gráfica del seno
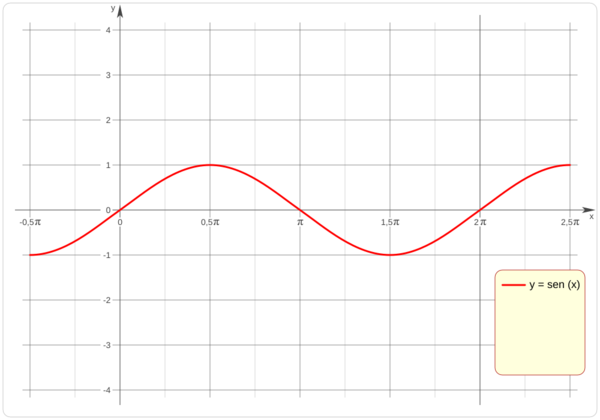
La gráfica de la función seno es una curva que sube y baja de forma regular, como una ola. Se llama sinusoide. Esta forma de onda es muy común en la naturaleza, como en las ondas de sonido, las ondas de luz o las mareas.
Otros temas relacionados
- Función impar
- Función periódica
- Sinusoide
- Período de oscilación
- Teorema del seno
- Trigonometría
- Función trigonométrica
Véase también
En inglés: Sine and cosine Facts for Kids
