Historia de la geometría para niños
La geometría es una de las ciencias más antiguas que existen. Al principio, era un conjunto de conocimientos prácticos para medir longitudes, áreas y volúmenes. Imagina que necesitabas saber cuánto terreno tenías o cuánto espacio ocupaba algo; ¡para eso servía la geometría!
La civilización babilónica fue una de las primeras en estudiar geometría. Cuando inventaron la rueda, empezaron a investigar las circunferencias y descubrieron el número pi (π). También crearon un sistema para medir ángulos y el tiempo, basándose en que el año tiene 365 días. Además, sabían cómo calcular el área de figuras como el trapecio.
En el antiguo Egipto, la geometría estaba muy avanzada. Los griegos, como el historiador Heródoto, contaban que los egipcios la habían "inventado". Usaban fórmulas prácticas para medir terrenos después de las inundaciones anuales del río Nilo. De hecho, la palabra "geometría" viene del griego y significa "medición de la tierra". Un ejemplo de su conocimiento es cómo trazaban líneas rectas usando una cuerda con nudos para formar triángulos perfectos.
Más tarde, en el siglo III antes de Cristo, un matemático griego llamado Euclides organizó la geometría de una manera muy lógica. Escribió un libro llamado Los Elementos, que fue la base de la geometría durante muchísimos siglos. En este libro, Euclides partía de ideas muy básicas y claras (llamadas postulados) y, a partir de ellas, demostraba todo lo demás.
El estudio de las estrellas (astronomía) y la creación de mapas (cartografía) también ayudaron a la geometría, ya que se necesitaban formas de ubicar planetas y estrellas. Mucho después, en el siglo XVII, René Descartes unió la geometría con el álgebra, creando la geometría analítica. Esto permitió representar figuras geométricas, como curvas, usando ecuaciones y números. Más tarde, matemáticos como Leonhard Euler y Carl Friedrich Gauss exploraron la estructura interna de las formas, lo que llevó a nuevas ramas como la topología y la geometría diferencial.
Contenido
Orígenes de la Geometría
Geometría en Babilonia

Los babilonios, conocidos por inventar la rueda, también investigaron la relación entre la longitud de una circunferencia y su diámetro, lo que les llevó a un valor aproximado de pi. Dividieron la circunferencia en 360 partes, dando origen al grado sexagesimal, que usamos hoy para medir ángulos. También sabían cómo dibujar un hexágono regular y tenían conocimientos sobre los "triángulos pitagóricos", mucho antes de que Pitágoras naciera. En 2021, se encontraron pruebas de que los babilonios ya usaban la trigonometría 1500 años antes que los griegos.
Geometría en Egipto
La geometría en el antiguo Egipto era muy práctica. Los egipcios usaban "recetas" o algoritmos para calcular volúmenes, áreas y longitudes. Esto les servía, por ejemplo, para medir y reconstruir las parcelas de tierra después de las inundaciones anuales del Nilo. De ahí viene el nombre "geometría", que significa "medición de la tierra".
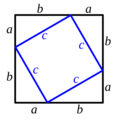
Para trazar líneas rectas y ángulos perfectos, los agrimensores egipcios usaban una cuerda con doce nudos a distancias iguales. Con ella, podían formar triángulos rectángulos con lados de 3, 4 y 5 unidades. Se cree que ellos ya conocían la relación numérica de estos lados (3² + 4² = 5²), que es una base del famoso Teorema de Pitágoras.
Geometría en Grecia
La geometría griega fue la primera en ser formal y lógica. Los griegos no solo querían saber cómo medir, sino también por qué las cosas eran así.
Antes de Euclides
Antes de Euclides, los matemáticos griegos ya buscaban la verdad de las ideas geométricas a través del razonamiento. Querían demostrar que una afirmación era cierta basándose en otras afirmaciones que ya sabían que eran verdad. Esto sentó las bases de la lógica matemática.
Euclides y Los Elementos
Euclides, que trabajó en la famosa Biblioteca de Alejandría, resolvió el problema de cómo empezar a demostrar cosas en geometría. Propuso un sistema donde algunas ideas básicas se aceptaban como verdaderas porque eran muy claras (los postulados). A partir de ellas, dedujo todos los demás resultados.
Su obra más importante, Los elementos, es un modelo de cómo construir un sistema de conocimiento paso a paso. Con solo cinco postulados y algunas definiciones, Euclides construyó toda la geometría y aritmética conocidas en su tiempo. Su libro, con trece volúmenes, fue la referencia principal de la geometría hasta el siglo XIX.
Uno de los postulados de Euclides, el quinto postulado, causó muchos debates. Aunque parecía cierto, muchos pensaban que quizás se podía demostrar a partir de los otros cuatro. Durante siglos, los matemáticos intentaron probar si este postulado era realmente necesario o si era un teorema que se podía deducir.
Después de Euclides
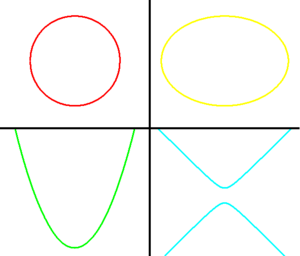
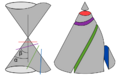
Después de Euclides, otros grandes matemáticos griegos continuaron desarrollando la geometría. Arquímedes estudió a fondo las secciones cónicas (formas que se obtienen al cortar un cono, como círculos, elipses, parábolas e hipérbolas). También introdujo curvas como la espiral que lleva su nombre y calculó el volumen de la esfera.
Apolonio de Perge también trabajó en las secciones cónicas y en cómo trazar líneas que tocan círculos (tangencias).
Tres problemas clásicos sin resolver
La geometría griega se encontró con tres problemas famosos que no pudo resolver usando solo la regla y el compás "ideales", que eran los únicos instrumentos permitidos.
- Duplicación del cubo: La leyenda cuenta que una peste asolaba Atenas y el oráculo de Delfos dijo que para detenerla debían duplicar el altar cúbico de Apolo en Delos. Los atenienses construyeron un altar con el doble de lado, pero el volumen resultó ser ocho veces mayor (porque 2x2x2=8). Nadie supo cómo construir un cubo con exactamente el doble de volumen que otro dado, usando solo regla y compás.
- Trisección del ángulo: Este problema consiste en dividir un ángulo cualquiera en tres partes iguales, usando solo regla y compás. Aunque es posible para algunos ángulos específicos, se demostró en el siglo XIX que es imposible de resolver para un ángulo cualquiera.
- Cuadratura del círculo: Se trata de construir un cuadrado que tenga exactamente la misma área que un círculo dado, usando solo regla y compás. Anaxágoras fue uno de los primeros en intentarlo. Este problema se convirtió en el símbolo de lo imposible en matemáticas. En 1882, se demostró que es imposible porque el número pi (π) es un número especial que no puede construirse con regla y compás.
Geometría en India
En la India, el texto Baudhayana Shulba Sutras, escrito entre los siglos VIII y V a. C., ya mencionaba los triángulos pitagóricos y el Teorema de Pitágoras.
Más tarde, en el año 628, el matemático Brahmagupta escribió una obra astronómica que incluía importantes ideas geométricas. Por ejemplo, su famoso teorema sobre los cuadriláteros cíclicos (figuras de cuatro lados inscritas en un círculo) y una fórmula para calcular su área.
Geometría en China
Uno de los textos matemáticos chinos más antiguos, el Suàn shù shū (186 a. C.), ya hablaba de progresiones geométricas. El astrónomo Zhang Heng (78-139 d. C.) usó fórmulas geométricas y fue el primero en intentar calcular el valor de pi con mayor precisión. Más tarde, Zu Chongzhi (429-500 d. C.) mejoró aún más la aproximación de pi.
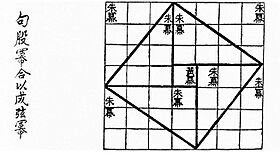
Los Nueve Capítulos sobre el Arte Matemático
Este importante libro chino, editado por Liu Hui en el siglo III d. C., contenía muchos problemas de geometría. Incluía cómo calcular áreas de cuadrados y círculos, volúmenes de figuras tridimensionales y el uso del Teorema de Pitágoras. Liu Hui también calculó pi con gran precisión y describió el principio de Cavalieri para calcular volúmenes.
Geometría en la Edad Media
Durante la Edad Media, las matemáticas avanzaron en la India y el mundo árabe, especialmente en Trigonometría y Álgebra. Sin embargo, en geometría no hubo muchas novedades. En Europa, aunque la geometría era una de las siete Artes liberales, las escuelas se limitaban a enseñar los Elementos de Euclides.
Geometría Proyectiva
En el Renacimiento, artistas y arquitectos como Leonardo da Vinci y Alberto Durero necesitaban nuevas formas de representar la realidad en sus obras. Esto llevó al estudio de la perspectiva y a la creación de la Geometría proyectiva. Sus principios fueron establecidos por Gérard Desargues en el siglo XVII. Esta nueva geometría fue estudiada por Blaise Pascal, pero no se hizo tan popular hasta el siglo XIX con Gaspard Monge y Jean-Victor Poncelet.
Geometría Cartesiana
La geometría analítica, creada por René Descartes, fue un gran cambio en la geometría moderna. Descartes propuso un nuevo método para resolver problemas geométricos usando ecuaciones algebraicas.
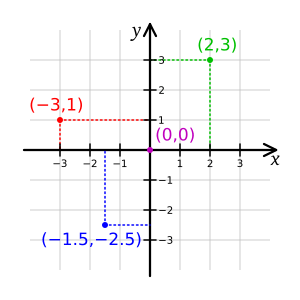
En este método, se usan dos líneas perpendiculares (llamadas ejes) en un plano. Cada punto del plano se puede ubicar con dos números, llamados coordenadas (x,y). La coordenada 'x' indica la distancia al eje vertical, y la 'y' la distancia al eje horizontal. Los signos positivo o negativo indican la dirección.
Lo más innovador de la geometría analítica es que permite representar figuras geométricas con ecuaciones. Por ejemplo, una línea recta se puede expresar con una ecuación de primer grado (como 2x + 6y = 0), y un círculo o una elipse con ecuaciones de segundo grado (como x² + y² = 4). Esto unió la geometría con el álgebra de una manera muy poderosa.
Evolución de la Geometría
El fin de un método
La geometría analítica cambió la forma de estudiar geometría. El antiguo método, que partía de axiomas y deducía teoremas, fue reemplazado por el método algebraico. Este nuevo enfoque estudiaba los objetos geométricos como representaciones de ecuaciones. El método antiguo solo volvió a usarse con las geometrías no euclidianas, pero ya no fue la principal herramienta de investigación.
Límites del álgebra
El método algebraico permitió estudiar curvas más complejas. Sin embargo, este método, que dio origen a la Geometría algebraica, tardó en desarrollarse plenamente. Esto se debió a la dificultad de resolver ecuaciones de quinto grado o mayores, un problema que no se solucionó hasta el siglo XIX.
El Cálculo Infinitesimal
El Cálculo Infinitesimal, desarrollado por Isaac Newton y Gottfried Leibniz, también tuvo una relación muy cercana con la geometría. Al principio, no se distinguía entre una curva y una función. Leonhard Euler fue el primero en ver la diferencia y en aplicar estos estudios a las superficies.
Más adelante, la geometría se usó mucho en la Mecánica y otras ramas de la Física, especialmente para resolver Ecuaciones Diferenciales. Se estudió la curvatura de las curvas, un concepto importante para entender cómo se doblan las formas.
Geometría Moderna
Carl Friedrich Gauss
Carl Friedrich Gauss fue un genio que hizo grandes aportaciones a la geometría. En su juventud, descubrió cómo construir un polígono regular de 17 lados, lo que lo llevó a dedicarse a las matemáticas.
Gauss también fue pionero en el análisis complejo, que estudia números que tienen una parte "imaginaria", dándoles una interpretación geométrica. Pero su mayor contribución a la geometría fue la creación de la geometría diferencial.
Gauss estableció la idea fundamental de la curvatura de una superficie. Gracias a esto, y al concepto de geodésica (la distancia más corta entre dos puntos sobre una superficie), demostró que existen superficies donde los triángulos formados por geodésicas no cumplen las reglas de Euclides. Esto significaba que era posible crear geometrías no euclídeas, es decir, geometrías diferentes a la de Euclides. Aunque Gauss no publicó sus descubrimientos de inmediato, fue el primero en concebir estas nuevas geometrías.
El fin de los grandes problemas antiguos
La discusión sobre el Quinto Postulado
Como se mencionó, Gauss fue el primero en crear una geometría donde el Quinto postulado de Euclides no se cumplía. Sin embargo, fueron János Bolyai y Nikolai Ivanovich Lobachevsky, de forma independiente, quienes publicaron sus propias geometrías no euclidianas.
Esto significaba dos cosas importantes: 1. El Quinto Postulado de Euclides es independiente de los otros cuatro; no se puede deducir de ellos. 2. Existen modelos de espacio donde, por un punto fuera de una línea, pueden pasar varias líneas paralelas a la dada, o ninguna. Esto es muy diferente a lo que nuestra intuición nos dice, pero es lógicamente válido.
Este descubrimiento causó una gran conmoción en las matemáticas del siglo XIX.
La trisección del ángulo y la duplicación del cubo
Un avance en el Álgebra por Évariste Galois en el siglo XIX resolvió estos dos problemas antiguos. Galois demostró que no se puede encontrar una fórmula general para resolver ecuaciones de quinto grado o mayores usando solo operaciones básicas.
Su teoría también demostró que todo lo que se puede construir con regla y compás tiene una forma matemática muy específica. La trisección de un ángulo y la duplicación de un cubo requieren polinomios que no tienen esa forma, por lo tanto, es imposible resolverlos solo con regla y compás.
La cuadratura del círculo
En 1882, el matemático Carl Louis Ferdinand von Lindemann demostró que el número pi (π) es un número "trascendente". Esto significa que no puede ser la raíz de ninguna ecuación polinómica con números enteros. Como resultado, no es posible construir un cuadrado con la misma área que un círculo dado usando solo regla y compás.
Geometría Intrínseca
La geometría intrínseca se interesa por las propiedades de las formas "desde dentro", sin depender de cómo se ven en un espacio más grande.
Leonhard Euler descubrió en 1752 una propiedad sorprendente de los poliedros (figuras con caras planas, como los cubos). Demostró que el número de vértices (puntos), aristas (líneas) y caras siempre cumple la relación V - A + C = 2. Esto era especial porque no dependía de las longitudes o áreas.
Más tarde, Carl Friedrich Gauss estableció el "teorema egregium", que significa "teorema notable". Este teorema dice que la curvatura de Gauss de una superficie no depende de cómo esa superficie esté colocada en el espacio. Es una propiedad propia de la superficie.
Nuevos espacios con propiedades extrañas
La geometría no euclidiana surgió de la imposibilidad de demostrar el Quinto postulado de Euclides. Matemáticos como Nikolai Ivanovich Lobachevsky y János Bolyai desarrollaron estas nuevas geometrías.
La cinta de Möbius, descubierta en 1858, es un ejemplo de una superficie "no orientable", lo que significa que no tiene un "lado" definido (interior o exterior). Si una hormiga camina sobre ella, puede recorrer toda la superficie sin cruzar un borde.
Bernhard Riemann
En 1854, Bernhard Riemann dio una conferencia muy importante sobre geometría. En ella, se preguntó qué pasaría si aumentáramos el número de dimensiones del espacio.
Variedades riemannianas y el tensor curvatura
Riemann introdujo el concepto de "variedad diferenciable", que es una generalización de la idea de superficie a cualquier número de dimensiones. Una superficie es una variedad de 2 dimensiones, una curva es de 1 dimensión.
Una "variedad riemanniana" es una variedad diferencial a la que se le añade una "métrica". Una métrica es como una regla que permite calcular longitudes y ángulos en cada punto de la variedad. Esto permite definir conceptos como la longitud de arco de una curva o el ángulo entre dos curvas. También se puede generalizar el concepto de geodésica, que es la curva más corta entre dos puntos sobre una superficie o variedad.
El punto clave de la conferencia de Riemann fue la definición del "tensor curvatura seccional", una herramienta que permite "medir la curvatura" de una variedad en cualquier número de dimensiones.
El modelo del Universo
En la segunda parte de su conferencia, Riemann se preguntó cómo debería ser el espacio físico en el que vivimos. Sus ideas, muy avanzadas para su época, fueron fundamentales para que Albert Einstein y Henri Poincaré desarrollaran la Teoría de la Relatividad.
La visión de Riemann permitió estudiar todas las geometrías, tanto la euclidiana como las no euclidianas, bajo un mismo enfoque. La geometría pasó a ser el estudio de las variedades, dejando de centrarse solo en triángulos, círculos y polígonos.
Felix Klein
Felix Klein fue otra figura clave en la geometría del siglo XIX. En 1871, descubrió que la geometría euclidiana y las no euclidianas podían verse como casos especiales de una geometría más general. Esto significaba que si la geometría euclidiana era lógica y no tenía contradicciones, las geometrías no euclidianas también lo eran.
Pero la contribución más importante de Klein fue su famoso Programa de Erlangen, donde dio una nueva definición de lo que es la geometría.
El Programa de Erlangen
En 1872, Klein propuso una idea sencilla pero muy profunda: cada geometría es el estudio de ciertas propiedades que no cambian cuando se aplican un tipo específico de transformaciones. A estas propiedades que no cambian las llamó "invariantes".
Klein descubrió que, por ejemplo:
- La geometría euclidiana estudia las propiedades que no cambian con los movimientos rígidos (como simetrías, giros y traslaciones).
- La Geometría proyectiva estudia las propiedades que no cambian con las proyectividades.
Klein afirmó que, en lugar de pensar "tengo una geometría, entonces hay un grupo de transformaciones", es al revés: uno elige qué tipo de transformaciones va a permitir (es decir, define el grupo), y a partir de ahí se construye toda la geometría. Este descubrimiento fue fundamental porque permitió clasificar las geometrías y entender que los diferentes métodos (sintético y algebraico) en realidad estudian la misma geometría.
Galería de imágenes
-
La Geometría como una de las Artes Liberales y Euclides.
-
Página de Analysis Geometrica, un tratado de geometría publicado en 1698 por el matemático español Antonio de Omerique.
Véase también
 En inglés: History of geometry Facts for Kids
En inglés: History of geometry Facts for Kids