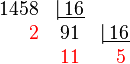Notación posicional para niños
La notación posicional es un sistema de numeración en el cual cada dígito posee un valor que depende de su posición relativa, la cual está determinada por la base, que es el número de dígitos necesarios para escribir cualquier número. Un ejemplo de numeración posicional es el habitualmente usado sistema decimal (base 10), necesitándose diez dígitos diferentes, los cuales deberán estar constituidos de un símbolo (grafema), cuyo valor en orden creciente es: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Para los números escritos en sistemas de bases menores, se usan solo los dígitos de menor valor; para los escritos con bases mayores que 10, se utilizan letras: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, ...
Contenido
Historia
El primer sistema de numeración posicional está documentado a comienzos del II milenio a. C. y fue utilizado por los eruditos de Babilonia. Posteriormente, a finales del I milenio a. C., lo emplearon los matemáticos chinos. Los sacerdotes astrónomos de la civilización maya lo usaron entre los siglos IV y IX de nuestra era: un sistema vigesimal con un dígito de valor cero, aunque con algunas peculiaridades que lo privaron de posibilidad operatoria.
La civilización india es la cuna de la notación posicional que usamos, aunque fueron los árabes los que impulsaron la gran innovación, utilizando la notación numérica indostánica: un sistema decimal con un dígito de valor nulo: el cero. Leonardo de Pisa (Fibonacci) introdujo en Occidente este sistema en el siglo XI.
Por cuestiones técnicas, en informática se optó por un sistema numérico en base dos, utilizándose solo dos dígitos: 0 y 1, pero empleando la notación posicional por su gran simplicidad operativa.
Características
Utilizando la notación posicional, el mismo dígito 5 toma diferente valor en los números 5, 50 y 500. Esto es una consecuencia de la descomposición de números en múltiplos de factores bn, donde b es la base y n cualquier número entero.
De forma más intuitiva, se descomponen en unidades de distintos órdenes, de tal forma que b unidades de cualquier orden equivalen a una de un orden inmediatamente superior. El orden que sirve de guía es la unidad propiamente dicha (b0)
Por convenio, los dígitos en esta notación se escriben de izquierda a derecha (incluso en idiomas que normalmente escriben de derecha a izquierda), empezando por los órdenes superiores y acabando en la unidad como tal, marcando la carencia de unidades con un 0 (cero). Así, en sistema decimal:
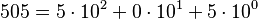
Si existen órdenes menores que la unidad, se escribe una coma (, ') o un punto en determinados idiomas (.) para separarlos de las unidades, y se continúa escribiendo de mayor a menor, acabando con las unidades de menor orden.
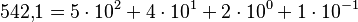
Los números negativos se marcan con un signo menos delante:
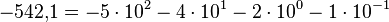
Si es necesario especificar la base, se escribe como subíndice entre paréntesis (lógicamente, en base decimal):

Los números periódicos (que poseen un grupo de cifras que se repite) tienen infinitos órdenes cada vez más pequeños cuyos múltiplos siguen un patrón. Este grupo de cifras (llamado período) se puede escribir una vez y marcar con un arco en la parte superior, o indicando con puntos suspensivos que el número continúa:
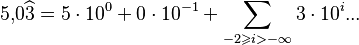
de forma menos rigurosa:
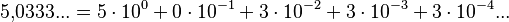
En la práctica se suele usar esta última solución o directamente redondear o truncar el número.
Tabla de conversión entre bases numéricas
|
Binario |
Base 3 |
Base 4 |
Base 5 |
Base 6 |
Base 7 |
Oct |
Base 9 |
Dec |
Base 11 |
Base 12 |
Base 13 |
Base 14 |
Base 15 |
Hex |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
10 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
11 |
10 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
100 |
11 |
10 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
|
101 |
12 |
11 |
10 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
|
110 |
20 |
12 |
11 |
10 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
|
111 |
21 |
13 |
12 |
11 |
10 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
|
1000 |
22 |
20 |
13 |
12 |
11 |
10 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
|
1001 |
100 |
21 |
14 |
13 |
12 |
11 |
10 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
|
1010 |
101 |
22 |
20 |
14 |
13 |
12 |
11 |
10 |
A |
A |
A |
A |
A |
A |
|
1011 |
102 |
23 |
21 |
15 |
14 |
13 |
12 |
11 |
10 |
B |
B |
B |
B |
B |
|
1100 |
110 |
30 |
22 |
20 |
15 |
14 |
13 |
12 |
11 |
10 |
C |
C |
C |
C |
|
1101 |
111 |
31 |
23 |
21 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
D |
D |
D |
|
1110 |
112 |
32 |
24 |
22 |
20 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
E |
E |
|
1111 |
120 |
33 |
30 |
23 |
21 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
F |
|
10000 |
121 |
100 |
31 |
24 |
22 |
20 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
10 |
Algoritmos para cambio de base
Estos algoritmos se basan en la descomposición en factores de bn arriba mencionada. Por comodidad, todos los cálculos se hacen en base decimal, pero los cálculos funcionarían igual en cualquier otra base.
De base hexadecimal a base decimal
Simplemente multiplíquese cada dígito por la potencia dependiente, y después se evalúe el resultado como en una cuenta normal, en base decimal.
![\mbox{5B2,E}_{(16)} = [5 \cdot 16^2 + 11 \cdot 16^1 + 2 \cdot 16^0 + 14 \cdot 16^{-1}]_{(10)} = [1280 + 176 + 2 + 0{,}875]_{(10)} = 1458{,}875_{(10)}](/images/math/6/5/5/655572462a428fbb156ebe339d4db05b.png)
(recuérdese que B(16) = 11(10); E(16) = 14(10))
De base decimal a base hexadecimal
Divídase el número por su base hasta que ya no sea posible. Leyendo el primer cociente y los restos en orden inverso, se puede leer el número en la base foránea.
Para decimales, son necesarios algoritmos más complejos.
Ventajas de la notación posicional
Mediante la notación posicional decimal se puede escribir cualquier valor numérico entero con solo diez dígitos diferentes (tantos como indica la base), por muy grande o pequeño que sea, aunque es imprescindible un dígito de valor nulo, el cero, para poder operar fácilmente.
Véase también
 En inglés: Place value Facts for Kids
En inglés: Place value Facts for Kids