Geometría diferencial para niños
En matemáticas, la geometría diferencial es una rama que estudia las formas y los espacios usando herramientas del análisis matemático (como el cálculo) y del álgebra. Imagina que quieres entender cómo se curvan las superficies o cómo se mueven las cosas en un espacio que no es plano. La geometría diferencial te da las herramientas para hacerlo.
Esta área de las matemáticas se enfoca en objetos llamados variedades diferenciables. Piensa en ellas como una versión más general de las superficies que conoces, pero que pueden tener muchas más dimensiones y no siempre están dentro de un espacio más grande. Por ejemplo, la superficie de la Tierra es una variedad.
Mientras que la topología diferencial se ocupa de las propiedades de las formas que no cambian si las estiras o las doblas sin romperlas, la geometría diferencial añade la posibilidad de medir cosas como distancias, ángulos y cómo de curvado está un espacio. Esto se logra añadiendo estructuras especiales, como una "métrica" o una "conexión".
La geometría diferencial es muy importante en la física, especialmente en la teoría de la relatividad general de Albert Einstein. En esta teoría, el espacio-tiempo (el espacio y el tiempo juntos) se describe como una variedad diferenciable. Esto ayuda a entender cómo la gravedad afecta el movimiento de los objetos. También se usa en química, economía, ingeniería, gráficos por ordenador y aprendizaje automático.
Contenido
Historia de la Geometría Diferencial
La historia de la geometría diferencial es muy antigua y está ligada al estudio de las formas y el espacio. Desde hace mucho tiempo, los matemáticos han intentado entender cómo medir y describir superficies curvas.
Primeros Pasos: Antigüedad hasta el Renacimiento
El estudio de las formas curvas comenzó en la antigüedad clásica. Los matemáticos griegos antiguos ya sabían mucho sobre la forma de la Tierra, que es una geometría esférica. Por ejemplo, Eratóstenes calculó la circunferencia de la Tierra hace más de 2000 años. Ptolomeo creó mapas usando la proyección estereográfica para representar la Tierra.
Desde los tiempos de Euclides, se sabía que una línea recta es el camino más corto entre dos puntos. Aplicando esto a la superficie de la Tierra, se descubrió que los grandes círculos (como el ecuador) son los caminos más cortos entre dos puntos en la superficie terrestre. Estas ideas fueron los cimientos de la geometría diferencial.
Arquímedes también usó un método llamado "agotamiento" para calcular áreas de formas curvas, como el círculo, y volúmenes de sólidos como esferas y conos.
Durante el Renacimiento, Gerardus Mercator desarrolló su famosa proyección de Mercator para hacer mapas. Él sabía que su mapa no podía representar perfectamente las distancias en la Tierra, porque es imposible aplanar una esfera sin distorsionarla. Esto es una idea clave en geometría diferencial.
La Era del Cálculo: Siglos XVII y XVIII
El verdadero avance de la geometría diferencial llegó con el desarrollo del cálculo por Gottfried Leibniz e Isaac Newton alrededor del año 1600. Gracias a la geometría analítica de René Descartes, que usaba coordenadas para describir formas, se pudieron estudiar curvas y superficies de manera más precisa.
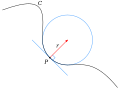
Matemáticos como Pierre de Fermat, Newton y Leibniz empezaron a investigar conceptos como los puntos de inflexión (donde una curva cambia de dirección) y los círculos osculantes (círculos que "tocan" una curva de la mejor manera posible en un punto, ayudando a medir su curvatura).
Los hermanos Bernoulli, Jacob y Johann, también hicieron contribuciones importantes. Johann Bernoulli escribió el primer libro de texto sobre cálculo diferencial, donde explicaba cómo calcular tangentes y puntos de inflexión en curvas.
Alexis Clairaut comenzó a estudiar las curvas espaciales (curvas en tres dimensiones) y la idea de "curvatura" y "doble curvatura", que son conceptos importantes para entender cómo se doblan las superficies.
Leonhard Euler, un alumno de Johann Bernoulli, hizo muchas contribuciones. Estudió las geodésicas (los caminos más cortos en una superficie curva) y desarrolló la idea de la "geometría intrínseca", que estudia las propiedades de una superficie desde dentro, sin necesidad de verla en un espacio más grande. Euler también notó que los objetos que se mueven sin fuerzas externas en una superficie siguen una trayectoria geodésica, una idea que más tarde sería fundamental para la teoría de la relatividad general de Einstein.
En el siglo XVIII, la escuela francesa, liderada por Gaspard Monge, también contribuyó al estudio de curvas y superficies.
Geometría Intrínseca y No Euclidiana: Siglo XIX
La geometría diferencial se convirtió en un campo de estudio propio en el siglo XIX, gracias a los trabajos de Carl Friedrich Gauss y Bernhard Riemann. También fue importante el trabajo de Nikolái Lobachevski sobre la geometría hiperbólica y la geometría no euclidiana.
En 1827, Gauss publicó Disquisitiones generales circa superficies curvas, una obra clave. Gauss es considerado el inventor de la geometría no euclidiana y de la geometría diferencial intrínseca. Introdujo conceptos como el mapa de Gauss y la curvatura de Gauss, y demostró el Theorema egregium, que muestra que la curvatura de Gauss es una propiedad intrínseca de la superficie (no depende de cómo esté incrustada en el espacio).
Gauss ya pensaba que la geometría euclidiana (la geometría plana que aprendemos en la escuela) no era la única posible. Al mismo tiempo, János Bolyai y Lobachevski descubrieron la geometría hiperbólica, demostrando que existían geometrías diferentes a la de Euclides. La geometría esférica de la Tierra es un ejemplo de geometría elíptica, otro tipo de geometría no euclidiana.
Bernhard Riemann, alumno de Gauss, llevó estas ideas más allá en su trabajo Sobre las hipótesis que fundamentan la geometría. Introdujo la métrica de Riemann y el tensor de curvatura de Riemann, y comenzó el estudio de la geometría diferencial en dimensiones superiores. Riemann también sugirió que las propiedades del espaciotiempo podrían medirse analizando las masas dentro de él, anticipando el principio de equivalencia de Einstein.
Después de Riemann, el estudio de la geometría diferencial se hizo más sistemático, usando el cálculo tensorial. Matemáticos como Sophus Lie y Jean Gaston Darboux desarrollaron la teoría de grupos de Lie. Elwin Christoffel introdujo los símbolos de Christoffel para describir la derivada covariante, una forma de derivar en espacios curvos. A finales del siglo XIX, Tullio Levi-Civita y Gregorio Ricci-Curbastro desarrollaron el cálculo tensorial, que fue el lenguaje que usó Einstein para su teoría de la relatividad general.
Variedades Diferenciables: Formas Generales

Una variedad es un objeto matemático que extiende la idea de curvas y superficies a más de dos dimensiones. Imagina que, aunque una variedad puede ser muy compleja en su conjunto, si te acercas mucho a cualquier punto de ella, se parece a un espacio plano.
Para describir una variedad, se usan "mapas" o "cartas". Una colección de estos mapas se llama "atlas". Cada mapa te permite ver una pequeña parte de la variedad como si fuera un trozo de un espacio plano.
Sobre una variedad, se pueden añadir diferentes estructuras:
- Una variedad topológica tiene una forma básica que permite definir qué puntos están "cerca" unos de otros.
- Una variedad diferenciable es una variedad topológica donde los mapas están conectados de forma "suave", es decir, puedes pasar de un mapa a otro sin saltos bruscos. Esto permite usar el cálculo.
- Una métrica Riemanniana es una estructura que permite medir distancias y ángulos en la variedad.
- Una conexión ayuda a entender cómo se relacionan los puntos cercanos y permite definir una forma especial de derivación llamada derivada covariante.
Aplicaciones de la Geometría Diferencial
La geometría diferencial tiene muchas aplicaciones importantes:
- En física, es fundamental para la teoría de la relatividad general de Einstein, donde describe la curvatura del espacio-tiempo causada por la masa y la energía. También se usa en la teoría cuántica de campos.
- En ingeniería, se utiliza para diseñar formas complejas, como las alas de los aviones o las carrocerías de los coches.
- En gráficos por ordenador y visión por ordenador, ayuda a crear modelos 3D y a analizar imágenes.
- En aprendizaje automático, se usa para entender la estructura de grandes conjuntos de datos.
Galería de imágenes
Véase también
 En inglés: Differential geometry Facts for Kids
En inglés: Differential geometry Facts for Kids