Teorema para niños
Un teorema es una idea o afirmación en matemáticas o lógica que ha sido demostrada como verdadera. Para demostrar un teorema, se parte de algunas ideas iniciales que se aceptan como ciertas (llamadas axiomas o hipótesis). A partir de ellas, se usa la lógica para llegar a una nueva afirmación que es la conclusión del teorema.
Piensa en un teorema como una regla o un hecho que ha sido probado paso a paso. Demostrar teoremas es muy importante en la lógica matemática. Los teoremas pueden escribirse con símbolos especiales o con palabras claras.
Los teoremas suelen tener condiciones iniciales que deben cumplirse. La parte final del teorema es una afirmación lógica o matemática que es verdadera si se cumplen esas condiciones. Lo interesante de un teorema es cómo conecta las ideas iniciales con la conclusión.
A veces, una afirmación es tan obvia después de demostrar un teorema que se le llama corolario. Es como una consecuencia inmediata del teorema principal.
Contenido
¿Qué es un Teorema?
Para que algo sea un teorema, necesita un conjunto de reglas básicas y un método para sacar conclusiones. Estas reglas básicas se llaman axiomas. El proceso de sacar conclusiones se llama inferencia. Así, un teorema se obtiene a partir de los axiomas o de otros teoremas que ya han sido demostrados.
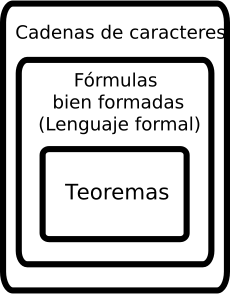
En la lógica, cualquier afirmación que se demuestra se considera un teorema. Una demostración es una serie de pasos lógicos. Cada paso es un axioma o una conclusión que se obtiene de pasos anteriores usando reglas de deducción. Si el último paso no es un axioma, entonces es un teorema.
En resumen, un teorema es una afirmación que no es un axioma, pero que puede ser el resultado final de una demostración lógica.
Teoremas y la Verdad
Hasta hace poco más de cien años, se pensaba que las matemáticas se basaban en verdades tan obvias que no necesitaban prueba. Por ejemplo, se creía que todos los números naturales tienen un siguiente, o que solo una línea puede pasar por dos puntos diferentes. Estas ideas básicas se llamaban postulados o axiomas.
Se pensaba que cualquier teorema demostrado a partir de estos axiomas era una verdad absoluta. Por ejemplo, que la suma de los ángulos interiores de un triángulo siempre es 180 grados.
Sin embargo, los matemáticos descubrieron que podían crear geometrías no euclidianas. En estas geometrías, la suma de los ángulos de un triángulo puede ser diferente de 180 grados, ¡y aun así no hay contradicciones! Esto mostró que la "verdad" de un teorema depende de las reglas (axiomas) que se usen.
Hoy en día, un teorema es una afirmación que se puede probar usando los axiomas y las reglas de inferencia de una teoría matemática específica. Así, el teorema del triángulo se reformula: Bajo los axiomas de la geometría euclidiana, la suma de los ángulos interiores de un triángulo es igual a 180 grados.
Esto significa que la validez de un teorema depende solo de que su demostración sea correcta. No depende de si los axiomas son "verdaderos" en el mundo real, sino de si la lógica es impecable. Esta forma de pensar permite usar resultados matemáticos en áreas que parecen no tener relación.
¿Cómo se presentan los Teoremas?
Muchos teoremas matemáticos son afirmaciones condicionales. Esto significa que tienen la forma "Si A, entonces B". Aquí, "A" es la hipótesis (la condición que debe cumplirse) y "B" es la conclusión (lo que se afirma si la hipótesis es verdadera). El teorema no dice que "B" sea siempre cierto, solo que "B" es cierto si "A" lo es.
Por ejemplo, el teorema "Si n es un número natural par, entonces n/2 es un número natural" tiene como hipótesis "n es un número natural par" y como conclusión "n/2 es también un número natural".
Aunque los teoremas se pueden escribir con símbolos, a menudo se explican con palabras para que sean más fáciles de entender. Lo mismo ocurre con las demostraciones. Los matemáticos prefieren una prueba que no solo demuestre que un teorema es válido, sino que también explique "por qué" es cierto.
Es común que una teoría matemática se base en un conjunto de axiomas. Estos axiomas son las ideas fundamentales de la teoría. La teoría de la prueba es una rama de las matemáticas que estudia estos lenguajes formales, axiomas y la estructura de las demostraciones.
Tipos de Teoremas

Algunos teoremas son "triviales" porque se derivan de las definiciones o axiomas de forma muy sencilla. No tienen ideas sorprendentes. Otros, en cambio, son "profundos". Sus demostraciones pueden ser largas y difíciles, o pueden conectar áreas de las matemáticas que parecían muy diferentes. Un teorema puede ser fácil de decir, pero muy difícil de probar. Un ejemplo famoso es el Último teorema de Fermat.
Hay teoremas cuyas demostraciones son tan complejas que solo se pueden verificar con la ayuda de computadoras. Dos ejemplos son el teorema de los cuatro colores y la conjetura de Kepler. Al principio, algunos matemáticos no aceptaban estas pruebas, pero ahora son más comunes.
Teoremas Relacionados
Si tenemos dos afirmaciones, p y q, podemos formar teoremas relacionados al intercambiar la hipótesis y la conclusión, o al usar sus negaciones:
- Teorema directo: Si p es cierto, entonces q es cierto.
- Teorema recíproco: Si q es cierto, entonces p es cierto.
- Teorema inverso: Si p no es cierto, entonces q no es cierto.
- Teorema contrarrecíproco: Si q no es cierto, entonces p no es cierto.
Terminología en Matemáticas
En matemáticas, no todas las afirmaciones demostradas se llaman teoremas. Solo las que son interesantes o importantes para la comunidad matemática. Las afirmaciones menos importantes tienen otros nombres:
- Lema: Es una afirmación más pequeña que se usa para demostrar un teorema más grande. A veces, un lema se vuelve tan importante que se le considera un teorema por sí mismo, como el lema de Gauss.
- Corolario: Es una afirmación que se deduce de forma muy sencilla de un teorema que ya ha sido demostrado.
- Proposición: Es una afirmación o resultado que no está directamente asociado a un teorema en particular. Muchos expertos usan "proposición" como sinónimo de "teorema".
- Conjetura o hipótesis: Es una afirmación matemática que se cree que es verdadera, pero que aún no ha sido demostrada. Ejemplos famosos son la conjetura de Goldbach y la hipótesis de Riemann.
Teoremas en Otras Ciencias
En campos como la física o la economía, a veces se usan afirmaciones importantes que se deducen de otras ideas básicas y se les llama "teoremas". Sin embargo, estas áreas no siempre están tan formalizadas como las matemáticas. Por eso, el término "teorema" debe usarse con cuidado en esos casos.
Presentación de un Teorema
Un teorema y su demostración suelen presentarse de la siguiente manera:
- Teorema (A veces se incluye el nombre de quien lo demostró y el año).
- Enunciado del teorema (La afirmación que se va a probar).
- Demostración
- Descripción de los pasos lógicos para probar el teorema.
- Fin
El final de la demostración se puede indicar con las letras Q.E.D. (que significa "lo que se quería demostrar") o con un símbolo como un cuadrado "□" o "∎".
Es común que antes de un teorema se den definiciones para explicar los términos que se usarán. También pueden presentarse lemas o proposiciones que se usarán en la demostración del teorema principal.
Los corolarios de un teorema se presentan justo después del teorema o después de su demostración. A veces, los corolarios también tienen sus propias demostraciones cortas.
Datos Curiosos sobre los Teoremas
Se calcula que cada año se demuestran más de 250,000 teoremas nuevos.
Hay una frase famosa que dice: "Un matemático es un dispositivo para convertir el café en teoremas". Se atribuye a menudo a Paul Erdős, un matemático muy conocido por la gran cantidad de teoremas que demostró y por su amor al café.
Algunos consideran que la demostración más larga de un teorema es la clasificación de grupos simples finitos. Ocupa miles de páginas en cientos de artículos escritos por muchos autores. Otro teorema con una demostración muy larga, generada por computadora, es el teorema de los cuatro colores. Es una de las demostraciones más largas que se conocen para un teorema que es fácil de entender.
Teoremas Famosos
Aquí tienes algunos de los teoremas más conocidos:
- Teorema de Pitágoras
- Teorema de Tales
- Teorema de Fermat-Wiles
- Teorema de Bayes
- Teorema del binomio
- Teorema de incompletitud de Gödel
- Teorema del límite central
- Teorema de los números primos
- Teorema de la divergencia
- Teorema de Stokes
- Teorema de Taylor
- Teorema de Rolle
Véase también
 En inglés: Theorem Facts for Kids
En inglés: Theorem Facts for Kids
- Axioma
- Sistema axiomático
- Tautología
- Teoría