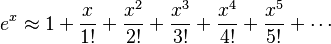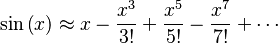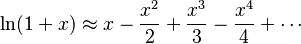robot de la enciclopedia para niños

Cálculo diferencial para niños

Enciclopedia para niños

El cálculo diferencial es una parte de las matemáticas que estudia cómo cambian las funciones. Imagina que tienes una gráfica que muestra cómo crece una planta con el tiempo. El cálculo diferencial te ayuda a saber qué tan rápido está creciendo la planta en un momento exacto. Su herramienta principal es la derivada.

Este campo de estudio se interesa mucho en los cambios muy, muy pequeños. Piensa en un cambio tan diminuto que casi llega a cero. Para entender esto, el cálculo diferencial usa un concepto clave llamado límite. Un límite es el valor al que se acerca algo, sin necesariamente tocarlo. Esta idea del límite es lo que hace que el cálculo diferencial sea diferente del álgebra.

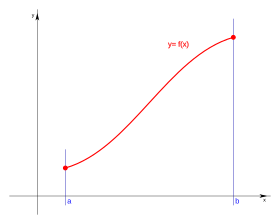
Desde el punto de vista de las funciones y la geometría, la derivada de una función en un punto específico nos dice qué tan rápido cambia esa función a medida que su variable se modifica. Es como medir la inclinación de una curva en un punto exacto. Esta inclinación se llama pendiente de la recta tangente a la gráfica en ese punto. Las derivadas también nos ayudan a saber si una función está subiendo o bajando, y dónde tiene sus puntos más altos o más bajos.

Lo contrario de una derivada se llama primitiva o integral.

Diferenciación: ¿Cuándo podemos calcular una derivada?

Una función puede ser "diferenciable" en un punto si su derivada existe en ese lugar. Si una función no es continua (es decir, tiene saltos o huecos) en un punto, entonces no puede ser diferenciable allí. Sin embargo, una función puede ser continua y aun así no ser diferenciable. Por ejemplo, la función que representa el valor absoluto de un número (como f(x) = |x|) es continua en x = 0, pero no es diferenciable en ese punto porque su gráfica tiene una "esquina" afilada.

La Derivada: Midiendo el Cambio Instantáneo

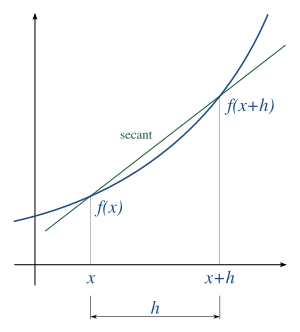
Archivo:Derivative
Recta secante entre los puntos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x+h) y f(x).

Las derivadas se definen usando el concepto de límite de las pendientes de las rectas secantes. Imagina que tienes una curva y quieres saber su inclinación en un punto exacto. Es difícil hacerlo directamente porque solo conoces ese punto.

Para resolver esto, tomamos dos puntos en la curva: el punto que nos interesa (x, f(x)) y otro punto muy, muy cercano (x+h, f(x+h)). La recta que une estos dos puntos se llama recta secante. Calculamos la pendiente de esta recta. Luego, hacemos que el segundo punto se acerque cada vez más al primer punto, es decir, hacemos que 'h' se vuelva muy, muy pequeño, casi cero.

La fórmula para la pendiente de la recta secante es: 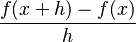f(x+h)-f(x)\over h

Cuando 'h' se acerca a cero, la recta secante se convierte en la recta tangente a la curva en el punto que nos interesa. La pendiente de esta recta tangente es la derivada de la función en ese punto. Se escribe así:

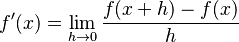
f'(x)=\lim_{h\to 0}{f(x+h)-f(x)\over h}

Si la derivada existe para cada punto 'x', entonces podemos decir que la derivada es una nueva función. Calcular esto directamente puede ser complicado porque no podemos dividir por cero. Por suerte, existen reglas generales que nos facilitan encontrar las derivadas de la mayoría de las funciones.

Funciones con Varias Variables

Cuando una función depende de más de una variable (por ejemplo, el volumen de una caja depende de su largo, ancho y alto), usamos el concepto de derivada parcial. Una derivada parcial nos dice cómo cambia la función cuando solo una de sus variables cambia, mientras las demás se mantienen fijas. Se representa con un símbolo especial, una 'd' redondeada: 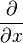\frac{\partial}{\partial x}.

Historia del Cálculo Diferencial

Los primeros problemas que llevaron al desarrollo del cálculo diferencial surgieron en la antigua Grecia, hace más de 2000 años. Sin embargo, no fue hasta el siglo XVII que se encontraron métodos sistemáticos para resolverlos. Esto fue gracias al trabajo de dos grandes matemáticos: Isaac Newton y Gottfried Wilhelm Leibniz.

Ellos unieron ideas de matemáticos anteriores y crearon lo que hoy conocemos como "diferenciación" e "integración". También desarrollaron reglas para trabajar con las derivadas y demostraron que la diferenciación y la integración son operaciones inversas.

Desde el siglo XVII, muchos matemáticos han contribuido al cálculo diferencial. En el siglo XIX, matemáticos como Augustin Louis Cauchy, Bernhard Riemann y Karl Weierstrass hicieron que el cálculo fuera más riguroso y preciso.

Aplicaciones Importantes del Cálculo Diferencial

La Recta Tangente a una Función

La recta tangente a una función en un punto es la mejor aproximación recta a la función en ese lugar. Es como si acercaras una regla a una curva en un punto y la regla tocara la curva solo en ese punto.

Si conocemos la ecuación de la recta tangente Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): T_a(x) a una función f(x) en un punto a, podemos usar esta recta para estimar el valor de la función cerca de ese punto. Cuanto más cerca estemos del punto a, más precisa será nuestra estimación.

Para una función f(x) que se puede derivar en el punto a, la ecuación de la recta tangente es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): T_a(x)=f(a)+f'(a)(x-a)

Usando Derivadas para Dibujar Gráficas

Las derivadas son muy útiles para entender y dibujar las gráficas de funciones. Por ejemplo, los puntos donde una función alcanza su valor más alto o más bajo (llamados extremos locales) tienen una primera derivada igual a cero.

Existen pruebas, como el criterio de la primera derivada y el criterio de la segunda derivada, que nos ayudan a saber si un punto es un máximo, un mínimo o ninguno de los dos. Una vez que encontramos estos puntos importantes, es mucho más fácil tener una idea general de cómo se ve la gráfica de la función.

Aproximación Local con Polinomios (Serie de Taylor)

Así como podemos aproximar una función con una recta tangente, si la función es "suave" (es decir, se puede derivar muchas veces), podemos aproximarla con polinomios de grados más altos (grado dos, tres, etc.). Esta aproximación se llama "desarrollo polinómico de Taylor".

La fórmula general es: 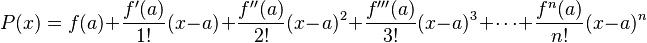P(x) = f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\cdots + \frac{f^{n}(a)}{n!}(x-a)^n

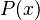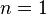Aquí, P(x) es el polinomio que mejor se acerca a la función en el punto x=a. Si n=1, esta fórmula nos da la ecuación de la recta tangente que vimos antes.

Cuando a=0, esta aproximación se llama "desarrollo de MacLaurin". Algunos ejemplos importantes son:

  • e^x \approx 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!}+ \cdots
  • \sin\left( x \right) \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots
  • \ln(1+x)\approx x -\frac{x^2}2+\frac{x^3}3-\frac{x^4}4+\cdots

El símbolo 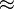\approx significa "aproximadamente igual". Si la función se puede derivar infinitas veces y añadimos infinitos términos al polinomio, entonces la aproximación se convierte en una igualdad exacta.

Encontrando Puntos Especiales en Funciones

FunEsc Dominio 04.svg

Cuando estudiamos una función, podemos identificar diferentes tipos de puntos:

  • Puntos frontera: Los límites de su dominio.
  • Puntos interiores: Los que están dentro del dominio.
  • Puntos críticos: Incluyen puntos singulares y estacionarios.
  • Puntos de inflexión: Donde la curva cambia su concavidad (de abrirse hacia arriba a abrirse hacia abajo, o viceversa).

Puntos Críticos

Un punto crítico es un punto singular o estacionario.

Puntos Singulares

Son los valores donde la derivada de la función 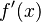f'(x) tiene algún tipo de interrupción o no existe.

Puntos Estacionarios

Son los valores de la variable donde la derivada 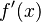f'(x) es igual a cero. Es decir, si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x_i)=0 , entonces 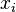x_i es un punto estacionario.

Si la segunda derivada de la función es positiva en un punto estacionario, ese punto es un mínimo local (el valor más bajo en esa zona). Si es negativa, es un máximo local (el valor más alto en esa zona). Si es cero, puede ser un máximo, un mínimo o un punto de inflexión. Encontrar estos puntos nos ayuda a resolver problemas de optimización, donde buscamos los valores más grandes o más pequeños posibles.

Galería de imágenes

  • NautilusCutawayLogarithmicSpiral

    La espiral logarítmica de la concha del Nautilus es una clásica imagen usada para representar el (de)crecimiento continuo, concepto clave del cálculo.

Véase también

Kids robot.svg En inglés: Differential calculus Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Cálculo_diferencial&oldid=4785150»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Cálculo diferencial para Niños. Enciclopedia Kiddle.