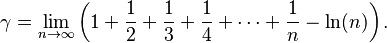Leonhard Euler para niños

Datos para niños Leonhard Euler
Leonhard Euler por Jakob Emanuel Handmann (hacia 1756) Deutsches Museum, Múnich
Información personal
Nombre de nacimiento	Leonhard Paul Euler
Nacimiento	15 de abril de 1707 Basilea, Suiza
Fallecimiento	18 de septiembre de 1783 San Petersburgo, Imperio ruso
Causa de muerte	Hemorragia cerebral
Sepultura	Smolensky Lutheran y Cementerio de San Lázaro de San Petersburgo
Residencia	Prusia, Rusia
Nacionalidad	Suiza
Religión	Protestantismo
Familia
Padres	Marguerite Brucker Paul Euler
Cónyuge	Katharina Gsell (1734-1773) Salome Abigail Gsell (1776-1783)
Hijos	Johann Euler
Educación
Educación	máster y doctor en Filosofía
Educado en	Universidad de Basilea
Supervisor doctoral	Johann Bernoulli
Información profesional
Área	Matemáticas, Física, y Filosofía
Cargos ocupados	Adjunct (1727-1730) Catedrático (desde 1731juliano, hasta 1741) Catedrático (desde 1766)
Empleador	Academia de Ciencias de Rusia Academia Prusiana de las Ciencias
Estudiantes doctorales	Johann Friedrich Hennert Nicolas Fuss Stepán Rumovski
Alumnos	Anders Johan Lexell, Stepán Rumovski, Johann Euler y Joseph-Louis Lagrange
Obras notables	teorema de Euler Teorema de rotación de Euler teorema geométrico de Euler Conjetura de Euler teorema de poliedros de Euler ecuaciones de Euler-Lagrange ecuación de Cauchy-Euler Función φ de Euler identidad de Euler Identidad de los cuatro cuadrados de Euler fórmula de Euler teorema de Euler función gamma integral de Gauss constante de Euler-Mascheroni Números afortunados de Euler diagrama de Euler circunferencia de los nueve puntos recta de Euler
Miembro de	Real Academia de las Ciencias de Suecia Academia Prusiana de las Ciencias (desde 1741) Royal Society (desde 1747) Academia de Ciencias de Francia (desde 1755) Academia de Ciencias de Turín (desde 1760) Academia Estadounidense de las Artes y las Ciencias (desde 1782)
Firma

Leonhard Paul Euler (Basilea, Suiza; 15 de abril de 1707 - San Petersburgo, Imperio ruso; 18 de septiembre de 1783) fue un matemático y físico suizo. Es considerado el matemático más importante del siglo XVIII y uno de los más grandes de la historia. Es muy conocido por el número de Euler (e), que aparece en muchas fórmulas de cálculo y física.

Euler vivió gran parte de su vida adulta en San Petersburgo (Rusia) y Berlín (Prusia). Hizo descubrimientos importantes en áreas como el cálculo y la teoría de grafos. También introdujo mucha de la terminología y notación matemática moderna, especialmente en el análisis matemático, como la idea de función matemática. Además, es famoso por sus trabajos en mecánica, óptica y astronomía.

Se calcula que todas sus obras completas podrían llenar entre sesenta y ochenta volúmenes. Una frase atribuida a Pierre Simon Laplace muestra la gran influencia de Euler: «Lean a Euler, lean a Euler, él es el maestro de todos nosotros».

La vida de Leonhard Euler

Sus primeros años y estudios

Leonhard Euler nació en Basilea, Suiza. Su padre, Paul Euler, era un pastor, y su madre, Marguerite Brucker, también era hija de un pastor. Tuvo dos hermanas menores. Poco después de su nacimiento, su familia se mudó al pueblo de Riehen, donde Euler pasó su infancia. El padre de Euler era amigo de la familia Bernoulli, una famosa familia de matemáticos. Entre ellos destacaba Johann Bernoulli, quien era considerado el matemático más importante de Europa en ese momento y tuvo una gran influencia en el joven Leonhard.

Euler comenzó su educación formal en Basilea, viviendo con su abuela materna. A los trece años, ingresó en la Universidad de Basilea. En 1723, obtuvo su título de maestro de Filosofía. En ese tiempo, Euler recibía clases particulares de Johann Bernoulli cada sábado. Bernoulli descubrió rápidamente el gran talento de su alumno para las matemáticas.

Al principio, Euler estudiaba teología, griego y hebreo, siguiendo los deseos de su padre, quien quería que fuera pastor. Pero Johann Bernoulli convenció a Paul Euler de que Leonhard estaba destinado a ser un gran matemático. En 1726, Euler terminó su doctorado con una tesis sobre la propagación del sonido. En 1727, participó en un concurso de la Academia de las Ciencias francesa para encontrar la mejor forma de colocar el mástil en un barco. Quedó en segundo lugar, detrás de Pierre Bouguer. Más tarde, Euler ganaría este premio doce veces.

Su etapa en San Petersburgo

Los hijos de Johann Bernoulli, Daniel y Nicolás, trabajaban en la Academia de las ciencias de Rusia en San Petersburgo. En julio de 1726, Nicolás falleció. Daniel ocupó el puesto de su hermano y recomendó a Euler para la vacante en Fisiología. En noviembre de ese año, Euler aceptó la oferta, aunque tardó en ir a San Petersburgo mientras intentaba, sin éxito, conseguir un puesto de profesor de Física en la Universidad de Basilea.

Sello del año 1957 de la antigua Unión Soviética conmemorando el 250.º aniversario del nacimiento de Euler. El texto dice: «250 años desde el nacimiento del gran matemático y académico Leonhard Euler».

Euler llegó a Rusia el 17 de mayo de 1727. Fue trasladado del departamento médico al de matemáticas, donde trabajó de cerca con Daniel Bernoulli. Euler aprendió ruso y se estableció en San Petersburgo. Incluso trabajó como médico para la Armada de Rusia.

La Academia de San Petersburgo, fundada por Pedro I de Rusia, buscaba mejorar la educación y la ciencia en Rusia. Para ello, atrajo a científicos extranjeros como Euler. La Academia tenía muchos recursos y una gran biblioteca. Admitía pocos estudiantes para facilitar la investigación y daba libertad a los profesores para sus estudios.

Sin embargo, la emperatriz Catalina I de Rusia, quien apoyaba la Academia, murió el mismo día que Euler llegó a Rusia. Su muerte dio más poder a la nobleza, ya que el nuevo emperador, Pedro II de Rusia, tenía solo doce años. La nobleza desconfiaba de los científicos extranjeros, redujo los fondos de la Academia y causó dificultades a Euler y sus colegas.

Las condiciones mejoraron un poco tras la muerte de Pedro II. Euler fue ascendiendo en la Academia, convirtiéndose en profesor de Física en 1731. Dos años después, Daniel Bernoulli regresó a Basilea, cansado de las dificultades en San Petersburgo. Euler lo sucedió como director del departamento de Matemáticas.

El 7 de enero de 1734, Euler se casó con Katharina Gsell (1707-1773). Ella era hija de un pintor suizo de la Academia de San Petersburgo. La pareja compró una casa junto al Río Nevá y tuvo trece hijos, aunque solo cinco llegaron a la edad adulta. El mayor, Johann Euler, fue matemático y astrónomo.

Su vida en Berlín

Preocupado por los cambios en Rusia, Euler se fue de San Petersburgo el 19 de junio de 1741. Aceptó un puesto en la Academia de Berlín, ofrecido por Federico II el Grande, rey de Prusia. Vivió veinticinco años en Berlín, donde escribió más de 380 artículos. También publicó dos de sus obras más importantes: la Introductio in analysin infinitorum (1748), sobre funciones matemáticas, y la Institutiones calculi differentialis (1755), sobre cálculo diferencial.

A Euler también se le ofreció ser tutor de la princesa de Anhalt-Dessau, sobrina de Federico. Euler le escribió más de 200 cartas, que luego se publicaron como Cartas de Euler sobre distintos temas de Filosofía Natural dirigidas a una Princesa alemana. Este libro explicaba temas de física y matemáticas, y mostraba la personalidad y creencias de Euler. Fue su obra más leída, publicada en Europa y Estados Unidos. La popularidad de estas Cartas demuestra la habilidad de Euler para explicar ciencia a un público general.

A pesar de su gran aporte a la Academia, Euler tuvo que dejar Berlín. Esto se debió, en parte, a un conflicto con el rey Federico. El rey veía a Euler como una persona poco sofisticada, especialmente comparado con los filósofos que había reunido en la Academia, como Voltaire. Euler, siendo un hombre religioso y trabajador, era muy tradicional en sus creencias, lo opuesto a Voltaire. Euler no era bueno en retórica y a veces debatía temas que no dominaba, lo que lo hacía blanco de los ataques de Voltaire. Por ejemplo, Euler tuvo discusiones sobre metafísica con Voltaire, de las que se retiraba molesto por su falta de habilidad para debatir. Federico también estaba descontento con las habilidades de ingeniería de Euler:

Quería tener una bomba de agua en mi jardín: Euler calculó la fuerza necesaria de las ruedas para elevar el agua a un depósito, desde el que caería después a través de canalizaciones para finalmente manar en el palacio de Sanssouci. Mi molino fue construido de forma geométrica y no podía elevar una bocanada de agua hasta más allá de cinco pasos hacia la reserva. ¡Vanidad de las vanidades! ¡Vanidad de la geometría!

Federico II el Grande

Problemas de visión

Retrato de Euler del año 1753 dibujado por Jakob Emanuel Handmann. El retrato sugiere problemas en el ojo derecho, así como un posible estrabismo. El ojo izquierdo parece sano, si bien más tarde Euler tuvo problemas de cataratas.

La vista de Euler empeoró a lo largo de su vida. En 1735, sufrió una fiebre grave, y tres años después quedó casi ciego del ojo derecho. Euler creía que esto se debía al trabajo de cartografía que hacía para la Academia de San Petersburgo.

La vista de su ojo derecho empeoró durante su estancia en Alemania. El rey Federico II lo llamaba el Cíclope. Más tarde, Euler desarrolló cataratas en su ojo izquierdo, el sano, lo que lo dejó casi ciego pocas semanas después del diagnóstico. A pesar de esto, sus problemas de visión no afectaron su productividad intelectual. Lo compensó con su gran capacidad de cálculo mental. Por ejemplo, podía calcular al instante preguntas de trigonometría y las primeras 6 potencias de los primeros 100 números primos sin papel ni lápiz.

Pasó los últimos años de su vida ciego, pero siguió trabajando. Dictó muchos de sus trabajos a su hijo mayor. Esto aumentó el respeto que la comunidad científica ya le tenía. El matemático francés François Arago dijo una vez:

Euler calculaba sin esfuerzo aparente, como los hombres respiran, o como las águilas se sostienen en el aire.

Regreso a Rusia y fallecimiento

Tumba de Euler en el Monasterio de Alejandro Nevski.

La situación en Rusia había mejorado mucho con Catalina la Grande. En 1766, Euler aceptó una invitación para volver a la Academia de San Petersburgo y vivir allí el resto de su vida. Sin embargo, su segunda etapa en Rusia estuvo marcada por la tragedia: un incendio en San Petersburgo en 1771 destruyó su casa y casi le cuesta la vida. En 1773, perdió a su esposa Katharina Gsell, después de cuarenta años de matrimonio. Euler se volvió a casar tres años después con Salome Abigail Gsell, hermana de su primera esposa. Este segundo matrimonio duró hasta la muerte del matemático.

El 18 de septiembre de 1783, Euler falleció en San Petersburgo tras sufrir un accidente cerebrovascular. Fue enterrado junto a su primera esposa en el Cementerio Luterano de la isla Vasilievski. Sus restos fueron trasladados más tarde al Monasterio de Alejandro Nevski.

El matemático y filósofo francés Nicolas de Condorcet escribió su elogio fúnebre para la Academia francesa:

…il cessa de calculer et de vivre — … dejó de calcular y de vivir.

Nikolaus von Fuss, ahijado de Euler y secretario de la Academia Imperial de San Petersburgo, escribió un relato de su vida y una lista de sus obras.

Contribuciones de Euler a las matemáticas y la ciencia

Ilustración de la obra Solutio problematis... a. 1743 propositi (Acta eruditorum, 1744).

Euler trabajó en casi todas las áreas de las matemáticas: geometría, cálculo, trigonometría, álgebra, teoría de números, además de física, teoría lunar y otras áreas. También hizo aportes importantes a la lógica matemática con su diagrama de conjuntos.

Fue uno de los matemáticos más productivos de la historia. Publicaba sin parar (unas 800 páginas de artículos al año en su época de mayor actividad, entre 1727 y 1783). Gran parte de su obra completa aún no se ha publicado. La recopilación y publicación de todos sus trabajos, llamados Opera Omnia, comenzó en 1911 y ya ha llegado a 76 volúmenes. Se le considera la persona con más trabajos y artículos en cualquier campo del saber. Si se imprimieran todos sus trabajos, muchos de ellos muy importantes, ocuparían entre 60 y 80 volúmenes. Según el matemático Hanspeter Kraft, presidente de la Comisión Euler de la Universidad de Basilea, no se ha estudiado más del 10% de sus escritos. Por todo esto, el nombre de Euler está asociado a muchísimas ideas matemáticas.

Se cree que fue quien dio origen al pasatiempo sudoku al crear una serie de reglas para el cálculo de probabilidades.

¿Qué notaciones matemáticas introdujo Euler?

Euler introdujo y popularizó varias formas de escribir en matemáticas en sus libros de texto. Lo más notable fue la idea de función matemática. Fue el primero en escribir para referirse a la función aplicada al valor . Esta nueva notación era más cómoda que los métodos anteriores de cálculo infinitesimal, iniciados por Newton y Leibniz.

También introdujo la notación moderna de las funciones trigonométricas, la letra (número e) como base del logaritmo natural, la letra griega para los sumatorios, y la letra para la unidad imaginaria. El uso de la letra griega (número π) para la relación entre la circunferencia y su diámetro también fue popularizado por Euler, aunque no fue el primero en usarla.

Avances en el análisis matemático

El desarrollo del cálculo era muy importante en el siglo XVIII. La familia Bernoulli había logrado muchos avances. Gracias a su influencia, el estudio del cálculo se convirtió en uno de los principales temas de trabajo de Euler. Aunque algunas de sus demostraciones no cumplen los estándares modernos de rigor matemático, sus ideas fueron grandes avances en este campo.

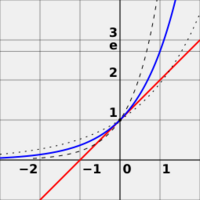
es el único número real a para el cual se cumple que el valor de la derivada de la función f (x) = a^x (curva azul) en el punto x = 0 es exactamente 1. En comparación se muestran las funciones 2^x (línea punteada) y 4^x (línea discontinua), que no son tangentes a la línea de pendiente 1 (en rojo).

El número e

Euler definió la constante matemática conocida como número . Es el número complejo para el cual la derivada (la pendiente de la línea tangente) de la función 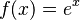en el punto 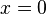es exactamente 1. Además, es el número real para el cual la función 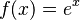es su propia derivada. La función 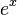también se llama función exponencial, y su función inversa es el logaritmo natural.

El número se puede representar de varias formas: como una serie infinita, un producto infinito, una fracción continua o como el límite de una sucesión. La representación más común en cálculo es el límite:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n, \quad e=\lim_{n\to 0}\left(1+n\right)^\frac{1}{n}

...y también la serie:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e=\sum_{n=0}^\infty \frac{1}{n!}\, .

Euler es muy conocido por su uso de las serie de potencias. Esto es, expresar funciones como una suma infinita de términos, como esta:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^x = \sum_{n=0}^\infty {x^n \over n!} = \lim_{n \to \infty}\left(\frac{1}{0!} + \frac{x}{1!} + \frac{x^2}{2!} + \cdots + \frac{x^n}{n!}\right).

Uno de los logros de Euler fue descubrir la expansión en series de potencias de la función arcotangente. Su uso audaz de las series de potencias le permitió resolver el famoso problema de Basilea en 1735, demostrando que:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim_{n \to \infty}\left(\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots + \frac{1}{n^2}\right) = \frac{\pi ^2}{6}.

Interpretación geométrica de la fórmula de Euler.

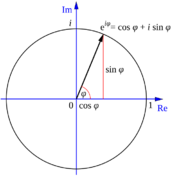
Euler introdujo el uso de la función exponencial y los logaritmos en las demostraciones. Descubrió cómo expresar funciones logarítmicas usando series de potencias. También definió logaritmos para números negativos y complejos, ampliando mucho su uso. Además, definió la función exponencial para números complejos y descubrió su relación con las funciones trigonométricas. Para cualquier número real φ, la fórmula de Euler dice que la función exponencial compleja se puede escribir así:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{i\varphi} = \cos \varphi + i\sin \varphi\, .

Un caso especial de esta fórmula (cuando Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \varphi = \pi ) es la identidad de Euler:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{i \pi} +1 = 0 \,

Richard Feynman la llamó «la fórmula más notable en matemáticas». Esto es porque relaciona las operaciones algebraicas principales con las importantes constantes 0, 1, , y . En 1988, los lectores de la revista The Mathematical Intelligencer la votaron como «la más bella fórmula matemática de la historia». Euler descubrió tres de las cinco primeras fórmulas de esa encuesta.

Euler también desarrolló la teoría de las funciones trascendentes (las que no se basan en operaciones algebraicas) al introducir la función gamma. Creó un nuevo método para resolver ecuaciones de cuarto grado. Descubrió cómo calcular integrales con límites complejos, lo que llevó al moderno análisis complejo. También inventó el cálculo de variaciones, incluyendo las ecuaciones de Euler-Lagrange.

Euler fue pionero en usar métodos analíticos para resolver problemas de teoría de números. Así, unió dos ramas de las matemáticas para crear un nuevo campo: la teoría analítica de números. Para esto, Euler creó la teoría de las series hipergeométricas, las series q, las funciones hiperbólicas trigonométricas y la teoría analítica de fracciones continuas. Por ejemplo, demostró que hay infinitos números primos usando la divergencia de series armónicas. También usó métodos analíticos para entender mejor cómo se distribuyen los números primos. El trabajo de Euler en esta área llevó al desarrollo del teorema de los números primos.

Otros aportes al cálculo

En su obra Introducción al análisis de los infinitos (1748), Euler hizo el primer estudio analítico completo del álgebra, la teoría de ecuaciones, la trigonometría y la geometría analítica.

Estudió el desarrollo de series de funciones y estableció que solo las series infinitas convergentes pueden evaluarse correctamente. También trabajó con superficies tridimensionales y demostró que las secciones cónicas se representan con la ecuación general de segundo grado en dos dimensiones.

Tenía una asombrosa habilidad con los números y un don para hacer cálculos mentales complejos. Se cuenta que una vez, cuando dos de sus alumnos no estaban de acuerdo en el resultado de una suma de series de diecisiete términos, se le preguntó a Euler. Él repasó el cálculo mentalmente y su respuesta fue la correcta.

También hizo aportes a la astronomía, la mecánica, la óptica y la acústica. Entre sus obras más destacadas están Instituciones del cálculo diferencial (1755), Instituciones del cálculo integral (1768-1770) e Introducción al álgebra (1770).

¿Qué descubrió Euler en la teoría de números?

El interés de Euler en la teoría de números surgió por la influencia de Christian Goldbach, su amigo en la Academia de San Petersburgo. Gran parte de los primeros trabajos de Euler en teoría de números se basaron en los de Pierre de Fermat. Euler desarrolló algunas ideas de Fermat, pero también descartó algunas de sus suposiciones.

Euler conectó la distribución de los números primos con sus ideas de análisis matemático. Demostró la divergencia de la suma de los inversos de los números primos. Al hacerlo, descubrió la conexión entre la función zeta de Riemann y los números primos. Esto se conoce como el producto de Euler para la función zeta de Riemann.

Euler también demostró las identidades de Newton, el pequeño teorema de Fermat, el teorema de Fermat sobre la suma de dos cuadrados. Hizo contribuciones importantes al teorema de los cuatro cuadrados de Joseph-Louis de Lagrange. También definió la función φ de Euler, que para cada número entero positivo, cuenta cuántos enteros positivos menores o iguales a él son coprimos (no tienen factores comunes) con él. Usando esta función, generalizó el pequeño teorema de Fermat a lo que se conoce como el teorema de Euler.

Contribuyó mucho a entender los números perfectos (teorema de Euclides-Euler), un tema que fascinó a los matemáticos desde los tiempos de Euclides. También avanzó en la investigación que más tarde se convertiría en el teorema de los números primos. Estos dos conceptos son teoremas fundamentales de la teoría de números, y sus ideas abrieron el camino para el matemático Carl Friedrich Gauss.

En 1772, Euler demostró que 2³¹ – 1 = 2 147 483 647 es un número primo de Mersenne. Este número fue el primo más grande conocido hasta 1867.

Aportes a la teoría de grafos y geometría

Mapa de la ciudad de Königsberg, en tiempos de Euler, que muestra, resaltado en verde, el lugar en donde se encontraban ubicados los siete puentes.

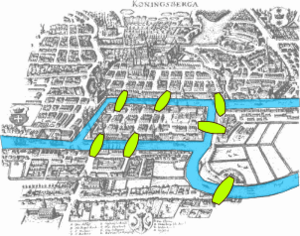
En 1736, Euler resolvió el famoso problema de los puentes de Königsberg. La ciudad de Königsberg, en Prusia Oriental (hoy Kaliningrado, Rusia), estaba en el río Pregel. Tenía dos grandes islas conectadas entre sí por un puente, y con las dos orillas del río por seis puentes más (siete puentes en total). El problema era si era posible recorrer todos los puentes una sola vez y volver al punto de partida. Euler demostró matemáticamente que no es posible. Esto se debe a que, en el modelo de grafo que representa el recorrido, el número de puentes es impar en más de dos de los puntos de conexión.

Esta solución se considera el primer teorema de la teoría de grafos y de grafos planares. Euler también introdujo el concepto de característica de Euler del espacio. Además, formuló una ecuación que relaciona el número de lados, vértices y caras de un polígono convexo con esta constante: el teorema de Euler para poliedros. Este teorema busca una relación entre el número de caras, aristas y vértices en los poliedros. Usó esta idea para demostrar que no existían más poliedros regulares que los sólidos platónicos ya conocidos. El estudio y la generalización de esta fórmula, especialmente por Cauchy y L'Huillier, dieron origen a la topología.

En el campo de la geometría analítica, descubrió que tres puntos importantes de un triángulo —baricentro, ortocentro y circuncentro— se encuentran en la misma línea recta. A esta línea se le llama «Recta de Euler» en su honor.

¿Cómo aplicó Euler las matemáticas?

Algunos de los mayores éxitos de Euler fueron al resolver problemas del mundo real usando el análisis matemático, lo que se conoce como matemática aplicada. Describió muchas aplicaciones de los números de Bernoulli, las series de Fourier, los diagramas de Venn, el número de Euler, las constantes y , las fracciones continuas y las integrales. Unió el cálculo diferencial de Leibniz con el método de fluxión de Newton. Desarrolló herramientas que facilitaron la aplicación del cálculo a problemas físicos. Euler ya usaba las series de Fourier antes de que Fourier las descubriera, y las ecuaciones de Lagrange del cálculo variacional, las ecuaciones de Euler-Lagrange.

Hizo grandes avances en la mejora de las aproximaciones numéricas para resolver integrales, inventando las aproximaciones de Euler. Las más notables son el método de Euler para resolver ecuaciones diferenciales ordinarias y la fórmula de Euler-Maclaurin. Este método consiste en aumentar la variable independiente paso a paso y encontrar la siguiente imagen con la derivada. También facilitó el uso de ecuaciones diferenciales, introduciendo la constante de Euler-Mascheroni:

Un interés particular de Euler fue aplicar las ideas matemáticas a la música. En 1739, escribió su obra Tentamen novae theoriae musicae. Esperaba incorporar las matemáticas a la teoría musical. Sin embargo, esta parte de su trabajo no atrajo mucha atención y fue descrita como «demasiado matemática para los músicos y demasiado musical para los matemáticos».

Aportes a la física y la astronomía

Euler ayudó a desarrollar la ecuación de la curva elástica, que es fundamental en la ingeniería. Además de aplicar sus herramientas analíticas a problemas de mecánica clásica, también las usó para los movimientos de los astros. Su trabajo en astronomía fue reconocido con varios premios de la Academia de Francia. Sus aportes incluyen la determinación precisa de las órbitas de los cometas y otros cuerpos celestes, mejorando la comprensión de su naturaleza. También calculó el paralaje solar. Formuló siete leyes o principios fundamentales sobre la estructura y dinámica del Sistema Solar. Afirmó que los cuerpos celestes y planetarios giran alrededor del Sol en órbitas elípticas. Sus cálculos también ayudaron a crear tablas de longitud más exactas para la navegación. También publicó trabajos sobre el movimiento de la Luna.

Euler hizo contribuciones importantes en óptica. No estaba de acuerdo con las teorías de Newton sobre la luz, que eran las más aceptadas en ese momento. Sus trabajos sobre óptica en la década de 1740 ayudaron a que la nueva teoría de la luz como onda, propuesta por Christiaan Huygens, se convirtiera en la dominante. Esta teoría se mantuvo hasta el desarrollo de la teoría cuántica de la luz.

En mecánica, Euler introdujo explícitamente los conceptos de partícula y masa puntual en su tratado de 1739. También usó la notación vectorial para la velocidad y la aceleración, sentando las bases de la mecánica hasta Lagrange. En la mecánica del sólido rígido, definió los «tres ángulos de Euler para describir la posición» y publicó el teorema principal del movimiento, que dice que siempre existe un eje de rotación instantáneo.

En hidrodinámica, estudió el flujo de un fluido ideal incompresible, detallando las ecuaciones de Euler de la hidrodinámica.

Más de cien años antes que Maxwell, Euler predijo el fenómeno de la presión de radiación, fundamental en la teoría unificada del electromagnetismo. En los cientos de trabajos de Euler, hay referencias a problemas y cuestiones muy avanzadas para su tiempo, que la ciencia de su época no podía resolver.

Lógica y diagramas de Euler

En el campo de la lógica, se le atribuye a Euler el uso de curvas cerradas para explicar el razonamiento silogístico (1768). Las representaciones de este tipo se llaman diagramas de Euler.

Arquitectura e ingeniería

En este campo, Euler desarrolló la ley que lleva su nombre sobre el pandeo de soportes verticales. Creó una nueva rama de la ingeniería con sus trabajos sobre la carga crítica de las columnas.

Creencias y filosofía de Euler

Euler y su amigo Daniel Bernoulli no estaban de acuerdo con las ideas de Leibniz y la corriente filosófica de Christian Wolff. Euler insistía en que el conocimiento se basa en leyes cuantitativas precisas, algo que el monismo y las teorías de Wolff no ofrecían. Sus creencias religiosas también pudieron influir en su rechazo a esas doctrinas, llegando a calificar las ideas de Wolff como «paganas y ateas». Sin embargo, tuvo una gran influencia debido al racionalismo temprano del filósofo René Descartes.

Gran parte de lo que sabemos sobre las creencias religiosas de Euler proviene de sus Cartas a una Princesa alemana y de un trabajo anterior llamado Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister (en español, Defensa de la revelación divina frente a las objeciones de los librepensadores). Estos trabajos muestran a Euler como un cristiano convencido que defendía la interpretación literal de la Biblia.

Obras importantes de Euler

Portada de la obra de Euler titulada Methodus inveniendi líneas curvas.

Euler tiene una bibliografía muy extensa. Aquí se mencionan algunas de sus obras más conocidas o importantes:

• Mechanica, sive motus scientia analytica exposita (1736).
• Solutio problematis ad geometriam situs pertinentis (1741).
• Methodus inveniendi líneas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti (1744).
• Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister — Defensa de la Revelación Divina frente a las objeciones del librepensador (1747).
• Introductio in analysin infinitorum (1748).
• Institutiones Calculi Differentialis (1765).
• Theoria motus corporum solidorum seu rigidorum (1765).
• Introducción a los elementos del álgebra (1765).
• Institutiones Calculi Integralis (1768-1770).
• Vollständige Anleitung zur Algebra (1770).
• Lettres à une Princesse d'Allemagne — Cartas a una Princesa alemana (1768-1772).

En 1911, la Academia Suiza de las Ciencias comenzó a publicar una colección definitiva de los trabajos de Euler titulada Opera Omnia. Hay un plan para ampliar la obra con la publicación de su correspondencia y manuscritos, aunque no hay fecha definida.

Reconocimientos y honores a Euler

Antiguo billete de 10 francos suizos con el retrato de Euler.

• La Iglesia Luterana conmemora a Euler en su Calendario de Santos el 24 de mayo. Esto es por ser un cristiano devoto (creyente en la infalibilidad de la Biblia) y un defensor convencido contra el ateísmo de su época.
• Varias calles en ciudades de todo el mundo llevan su nombre, como en París (Francia), Basilea (Suiza), Binzen (Alemania), Ciudad de México (México), Buenos Aires (Argentina), Padua (Italia) o Englewood (Estados Unidos).
• En su honor, Euler apareció en la sexta serie de los billetes de 10 francos suizos.
• Numerosos sellos postales de Suiza, Alemania y Rusia llevan su imagen.
• El cráter lunar Euler fue nombrado en su honor.
• El asteroide (2002) Euler también lleva su nombre por el gran matemático.

Véase también

En inglés: Leonhard Euler Facts for Kids