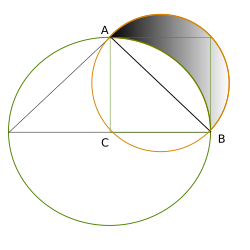Cuadratura del círculo para niños
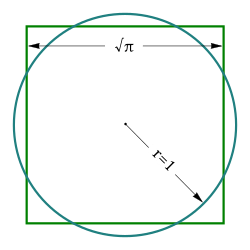
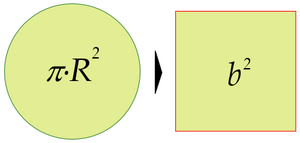
La cuadratura del círculo es uno de los tres problemas clásicos de la matemática antigua. Consiste en construir un cuadrado que tenga exactamente la misma área que un círculo dado. Para esto, solo se permite usar una regla y compás en un número limitado de pasos.
Este problema es similar a "rectificar la circunferencia". Esto significa construir una línea recta que mida lo mismo que el borde de un círculo. Ambos problemas están relacionados con el número pi (π). Pi es un número muy importante en matemáticas.
Desde 1882, sabemos que este problema no tiene solución si solo usamos regla y compás. El matemático alemán Carl Louis Ferdinand von Lindemann demostró que el número pi es un "número trascendente". Esto significa que no se puede obtener con operaciones básicas y raíces cuadradas.
La cuadratura del círculo fue un desafío muy popular durante siglos. Muchos matemáticos y aficionados intentaron resolverlo sin éxito. Por eso, la frase "cuadrar el círculo" se usa hoy como una metáfora. Significa intentar una tarea que no tiene solución.
Contenido
Historia de la cuadratura del círculo
La búsqueda de la cuadratura del círculo tiene una historia muy larga. Desde la antigüedad, la gente ha intentado resolver este misterio.
Orígenes antiguos y aproximaciones
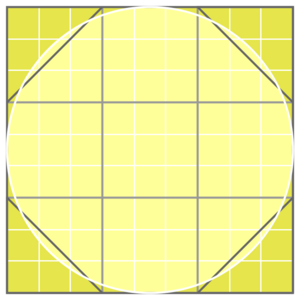
Un círculo con diámetro 9 inscrito en un cuadrado con longitud de lado 9, que se divide en nueve cuadrados más pequeños con longitud de lado 3.
El área del círculo corresponde aproximadamente a la de un octágono (irregular) (de 7x9) y algo más precisamente, a la de un cuadrado con una longitud de lado 8 (64)
Las culturas antiguas ya buscaban cómo calcular el área de los círculos. Por ejemplo, en el Papiro de Ahmes (hace unos 3600 años), se muestra un método. Se dividía el diámetro de un círculo en 9 partes. El área de un círculo con diámetro 9 es aproximadamente 63.62. Este valor se acercaba al área de un cuadrado de lado 8, que es 64.
Otro método antiguo usaba un octógono irregular. Se cortaban partes de un cuadrado de 9x9 para formar una figura de 63 unidades de área. Estas soluciones eran prácticas y se obtenían por experiencia. No se distinguía entre una solución exacta y una aproximación.
El pensamiento griego y los números irracionales
Las matemáticas con razonamiento lógico y demostraciones surgieron en Grecia. Esto ocurrió a partir del siglo VI antes de Cristo. Pensadores como Tales de Mileto y los pitagóricos fueron pioneros.
Un descubrimiento importante fue el de los "números inconmensurables". Esto se atribuye a Hípaso de Metaponto. Se dieron cuenta de que algunas longitudes, como la diagonal de un cuadrado, no podían expresarse como una fracción de números enteros. Esto fue sorprendente. Antes, se pensaba que todas las longitudes podían compararse con números enteros.
Este descubrimiento hizo que la geometría fuera más importante que la aritmética. Los problemas se resolvían dibujando figuras. Los tres problemas clásicos de la matemática antigua surgieron en el siglo V antes de Cristo. Además de cuadrar el círculo, estaban la trisección del ángulo y la duplicación del cubo.
Al principio, se permitían otras herramientas además de la regla y el compás. Pero con el tiempo, se hizo más estricta la regla de usar solo estas dos herramientas.
Primeros intentos de solución
El filósofo Anaxágoras (alrededor del 430 a.C.) fue uno de los primeros en escribir sobre la cuadratura del círculo. Sin embargo, no se tienen detalles de su trabajo.
Las fuentes más claras sobre los primeros intentos vienen de comentarios posteriores. Los trabajos más importantes del siglo V antes de Cristo son de Hipócrates de Quíos, Antifonte, Brisón de Heraclea e Hipias de Élide.
Hipócrates de Quíos encontró una forma de cuadrar áreas con bordes curvos. Estas áreas se llaman "lúnulas de Hipócrates". Demostró que algunas de estas lúnulas podían convertirse en un cuadrado. Sin embargo, esto no sirvió para cuadrar el círculo completo.
Antifonte tuvo la idea de aproximar el círculo con polígonos inscritos. Brisón de Heraclea mejoró esto usando también polígonos que rodeaban el círculo.
Hipias de Élide inventó una curva llamada "cuadratriz de Hipias". Con ella, se podía resolver la trisección del ángulo. Más tarde, Dinóstrato descubrió que esta curva también podía ayudar a construir un segmento relacionado con pi. Sin embargo, como la curva no se puede dibujar solo con regla y compás, no era una solución "clásica".
Los aportes de Arquímedes
Arquímedes escribió un tratado llamado "Medición circular". En él, demostró tres ideas clave:
- El área de un círculo es igual al área de un triángulo rectángulo. Un lado de este triángulo es el radio del círculo y el otro es la circunferencia.
- El área de un círculo se relaciona con el cuadrado de su diámetro de forma aproximada.
- La circunferencia de un círculo es un poco más de 3 veces su diámetro. Dio una aproximación muy buena: 22/7 (aproximadamente 3.143). Este valor todavía se usa hoy.
Arquímedes usó la idea de Brisón de Heraclea. Aproximó el círculo con polígonos de muchos lados, tanto dentro como fuera del círculo. Así, pudo estimar el valor de pi.
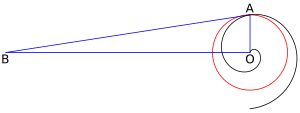
También describió la espiral arquimediana. Demostró que con esta espiral se podía encontrar una línea recta del mismo largo que la circunferencia de un círculo. Pero, al igual que la cuadratriz, esta espiral no se puede dibujar solo con regla y compás.
En la Edad Media, hubo más interés en las matemáticas antiguas. Surgieron nuevos trabajos sobre la cuadratura del círculo. Sin embargo, muchos pensaron que el valor de Arquímedes (22/7) era exacto, lo cual fue un error.
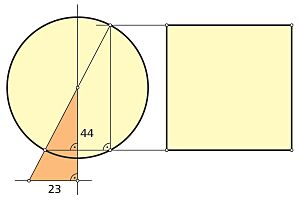
Franco de Lieja fue uno de los primeros en la Edad Media en revisar el problema. En 1050, publicó su obra "De quadratura circuli". Propuso una solución basada en dividir un círculo en 44 sectores y unirlos para formar un rectángulo. Pero su método tenía fallos.
Otros pensadores, como Nicolás de Cusa, también intentaron aproximaciones. Él usó polígonos con más y más lados. Sin embargo, sus cálculos no fueron precisos.
Avances en la era moderna
Desde el siglo XVI, los métodos para calcular figuras circulares mejoraron. Se desarrollaron nuevas formas de aproximación y el análisis matemático.
Willebrord Snel van Royen (Snellius) encontró una forma de obtener límites más precisos para la longitud de un arco. Christiaan Huygens luego demostró rigurosamente estos hallazgos. Con su método, la precisión era cuatro veces mejor que la de Arquímedes.
Luego, se usaron series infinitas para calcular pi. François Viète encontró una representación exacta de pi con un producto infinito. John Wallis y William Brouncker también encontraron fórmulas.
James Gregory y Gottfried Leibniz descubrieron una serie para calcular el arco tangente. Esta serie, aunque lenta, permitió calcular pi con muchos decimales. A principios del siglo XVIII, ya se conocían más de 100 dígitos de pi.
El problema algebraico y la irracionalidad de pi
Para resolver el problema, era necesario entender qué significaba "construible" en términos de álgebra. René Descartes introdujo el sistema de coordenadas. Esto permitió describir líneas y círculos con ecuaciones.
Se descubrió que las longitudes que se pueden construir con regla y compás son "números algebraicos". Estos números son soluciones de ecuaciones con coeficientes racionales. Los números que no son algebraicos se llaman "trascendentes". Por lo tanto, no se pueden construir longitudes trascendentes con regla y compás.
Leonhard Euler hizo descubrimientos fundamentales sobre pi y el número "e". En 1766, Johann Heinrich Lambert demostró que "e" y pi son irracionales. Esto significa que no pueden representarse como una fracción de números enteros. Adrien-Marie Legendre luego confirmó la irracionalidad de pi al cuadrado.
Hasta mediados del siglo XIX, no se sabía si existían números trascendentes. Joseph Liouville demostró su existencia.
La prueba de la imposibilidad
Finalmente, en 1882, Carl Louis Ferdinand von Lindemann demostró que pi no es un número algebraico, sino trascendente. Esto significó que no es posible cuadrar el círculo usando solo regla y compás.
Lindemann usó un resultado de Charles Hermite, quien había demostrado que el número "e" es trascendente. Basándose en esto, Lindemann probó el teorema de Lindemann–Weierstrass. Este teorema ayudó a demostrar que pi es trascendente.
La prueba de Lindemann se simplificó con el tiempo, con aportes de matemáticos como David Hilbert.
Popularidad del problema
La cuadratura del círculo fue muy popular. Muchos aficionados intentaron resolverlo, creyendo haberlo logrado.
En los siglos XVIII y XIX, hubo muchos trabajos de aficionados. La Academia de Ciencias de Francia incluso tuvo que anunciar en 1775 que ya no revisarían supuestas soluciones.
Incluso después de la prueba de Lindemann en 1882, se siguieron publicando supuestas cuadraturas. Hoy, estos intentos fallidos son parte de la matemática recreativa.
Una razón de su atractivo es que parece un problema sencillo de entender. Además, se creía que resolverlo podría traer una gran recompensa económica. Esta idea era falsa.
Famosas "cuadraturas del círculo"
Un ejemplo famoso fue el filósofo inglés Thomas Hobbes. Publicó una solución en 1665, pero fue refutada por John Wallis. Esto llevó a una larga discusión entre ellos.
El médico estadounidense Edward J. Goodwin publicó una cuadratura en 1894. Su trabajo se contradecía. Fue la base de un proyecto de ley en Indiana en 1897, el llamado "Proyecto de ley de Indiana sobre pi". Este proyecto buscaba hacer ley los hallazgos de Goodwin.
Arte y cultura
La cuadratura del círculo ha aparecido en el arte y la literatura.
- En la comedia "Las aves" de Aristófanes (siglo V a.C.), un personaje habla de hacer que "el círculo se convierta en un cuadrado".
- En 1321, Dante Alighieri en su "Divina comedia" comparó la cuadratura del círculo con algo imposible de entender para el ser humano.
- En la novela "Ulises" de James Joyce (1922), el protagonista, Leopold Bloom, intenta cuadrar el círculo para hacerse rico, pero fracasa.
Construcciones aproximadas
Aunque no hay una solución exacta con regla y compás, existen construcciones aproximadas. Estas son lo suficientemente precisas para muchos usos.
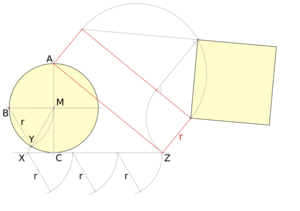
Construcción de Kochański
El matemático polaco Adam Adamandy Kochański descubrió una solución aproximada en 1685. Permite obtener una línea recta que es casi la mitad de la circunferencia de un círculo. Esta construcción aproxima el número pi con cuatro decimales.
- Para un círculo con radio de 100 metros, el error en el lado del cuadrado sería de aproximadamente -1.7 milímetros.
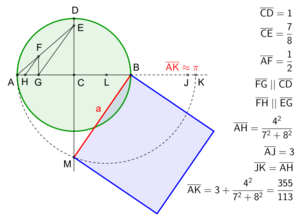
Construcción de Jacob de Gelder
En 1849, el matemático neerlandés Jacob de Gelder publicó una construcción simple. Se basa en una aproximación de pi que ya tenía seis decimales exactos. Esta aproximación viene del matemático chino Zu Chongzhi del siglo V.
- Para un círculo con radio de 100 kilómetros, el error en el lado del cuadrado sería de aproximadamente 7.5 milímetros.
Construcción de Hobson
El matemático británico E. W. Hobson encontró una construcción muy sencilla en 1913. Solo necesita tres arcos y dos segmentos en ángulo recto para encontrar el lado del cuadrado.
- Para un círculo con radio de 100 metros, el error en el lado del cuadrado sería de aproximadamente 1.4 milímetros.
Construcciones de Ramanujan
En 1913, el matemático indio Srinivasa Ramanujan también presentó una construcción aproximada. Su método era muy preciso.
- Ramanujan dijo que para un círculo de 140,000 millas cuadradas, el lado del cuadrado construido solo se desviaría una pulgada del valor real.
En 1914, Ramanujan dio otra construcción. Esta aproximación de pi se acerca a los ocho dígitos exactos.
- Para un círculo con radio de 10,000 kilómetros, el error en el lado del cuadrado sería de aproximadamente -2.8 milímetros.
Construcción de Louis Loynes
Louis Loynes publicó un método más simple en 1961. Su aproximación de pi es ligeramente mejor que la de Kochański.
- Para un círculo con radio de 1 kilómetro, el error en el lado del cuadrado sería de aproximadamente -3 milímetros.
Métodos no clásicos
Si se permite usar otras herramientas además de la regla y el compás, sí es posible cuadrar el círculo de forma exacta.
Uso de cuadraturas especiales
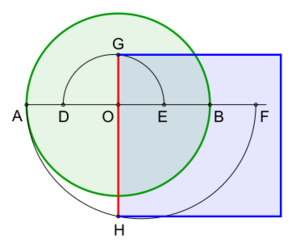
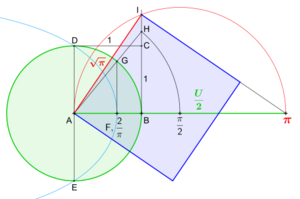
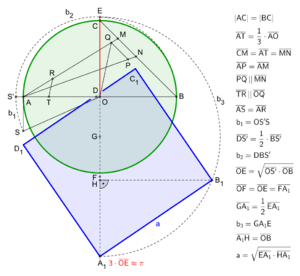
Con la ayuda de curvas especiales llamadas "cuadratrices", se puede cuadrar un círculo exactamente. Estas curvas se pueden dibujar con plantillas o dispositivos especiales. Ejemplos antiguos son la cuadratriz de Hipias y la espiral de Arquímedes.
La imagen muestra cómo cuadrar el círculo usando la cuadratriz de Hipias. Una vez que se construye el número pi con la cuadratriz, se puede encontrar la raíz cuadrada de pi. El cuadrado con este lado tendrá exactamente la misma área que el círculo.
Variantes del problema
Existen otras versiones del problema de la cuadratura.
El problema de la cuadratura del círculo de Tarski
En 1925, Alfred Tarski propuso un problema diferente. Quería saber si un círculo podía dividirse en partes y luego reordenarse para formar un cuadrado. Las partes no podían estirarse.
En 1989, Miklós Laczkovich encontró la solución. Demostró que sí es posible. Cortó el círculo en un número muy grande de partes (10^50). Sin embargo, esta demostración usa un concepto matemático avanzado llamado "axioma de elección".
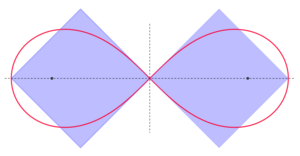
Cuadratura de la lemniscata
A diferencia del círculo, para una lemniscata de Bernouilli (una curva con forma de ocho), sí es posible construir dos cuadrados que tengan la misma área que la curva. Los lados de estos cuadrados son iguales al radio mayor de la lemniscata.
Ver también
- Número π
- Cuadratura del rectángulo
- Cuadratura del cuadrado
- Cuadratura de los polígonos
- Otras construcciones imposibles con regla y compás:
- La duplicación del cubo
- La trisección del ángulo
Véase también
 En inglés: Squaring the circle Facts for Kids
En inglés: Squaring the circle Facts for Kids