Algoritmo símplex para niños
En el mundo de las matemáticas, el algoritmo símplex es un grupo de métodos muy útiles para resolver problemas de programación lineal. Estos problemas buscan encontrar el mejor resultado posible (como el valor más alto o más bajo) de una función que tiene reglas sencillas y directas, llamadas "lineales". Imagina que tienes un conjunto de variables y quieres que cumplan ciertas condiciones (como "no puedes usar más de 100 gramos de un ingrediente"). El algoritmo símplex te ayuda a encontrar la mejor combinación de esas variables.
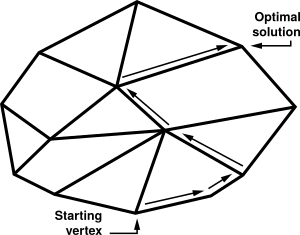
El algoritmo símplex original fue creado por el matemático estadounidense George Dantzig en 1947. Este método funciona explorando los "vértices" (las esquinas) de una figura geométrica llamada poliedro. Este poliedro representa todas las soluciones posibles que cumplen con las condiciones del problema. El algoritmo se mueve de una esquina a otra, buscando la que dé el mejor resultado.
Existe otro método con un nombre parecido, el método de Nelder-Mead (1965), pero no está relacionado con el algoritmo símplex de Dantzig. Este otro método también busca el mejor punto de una función, pero lo hace de una manera diferente, usando una figura llamada "símplex".
El algoritmo del método símplex fue reconocido como uno de los 10 algoritmos más importantes del siglo XX.
Contenido
¿Qué es el Algoritmo Símplex?
El algoritmo símplex es una herramienta poderosa para resolver problemas donde queremos maximizar (hacer lo más grande posible) o minimizar (hacer lo más pequeño posible) algo. Por ejemplo, una empresa podría querer maximizar sus ganancias o minimizar sus costos de producción.
Para que el algoritmo funcione, el problema debe estar planteado de una forma específica, usando ecuaciones e inecuaciones lineales. Esto significa que las relaciones entre las variables son directas, sin curvas ni potencias.
¿Para qué sirve el Algoritmo Símplex?
Este algoritmo se usa en muchos campos para tomar decisiones importantes. Algunos ejemplos son:
- Producción: Una fábrica puede usarlo para decidir cuánto de cada producto debe fabricar para obtener la mayor ganancia, considerando la cantidad de materiales y el tiempo disponible.
- Logística: Ayuda a las empresas a planificar las rutas de entrega para que los camiones gasten menos combustible o lleguen más rápido.
- Finanzas: Puede usarse para decidir cómo invertir dinero en diferentes opciones para obtener el mayor rendimiento con el menor riesgo.
- Asignación de recursos: Permite distribuir recursos limitados (como personal o maquinaria) de la manera más eficiente.
Conceptos Clave del Símplex
Para entender cómo funciona el algoritmo símplex, es útil conocer algunos términos:
Forma Estándar y Canónica
Antes de aplicar el algoritmo, los problemas de programación lineal se transforman en una "forma estándar" o "forma canónica". Esto significa que todas las condiciones (restricciones) se escriben de una manera específica, a menudo convirtiendo las desigualdades (como "menor o igual que") en igualdades, añadiendo variables especiales llamadas "variables de holgura" o "variables de excedente".
- Variables de holgura: Se añaden cuando una restricción es "menor o igual que" (≤). Representan la cantidad que "sobra" para llegar al límite.
- Variables de excedente: Se restan cuando una restricción es "mayor o igual que" (≥). Representan la cantidad que "excede" el límite mínimo.
- Variables artificiales: Se usan en algunos casos para ayudar al algoritmo a empezar, especialmente cuando las restricciones son de igualdad (=) o "mayor o igual que" (≥).
Variables Básicas y No Básicas
En cada paso del algoritmo, algunas variables tienen un valor diferente de cero (son las "variables básicas") y otras tienen un valor de cero (son las "variables no básicas"). El algoritmo va cambiando cuáles variables son básicas y cuáles no, buscando la mejor solución.
- Variables de entrada: Son variables no básicas que el algoritmo decide "activar" (darles un valor diferente de cero) para intentar mejorar el resultado.
- Variables de salida: Son variables básicas que el algoritmo decide "desactivar" (hacerlas cero) para dar espacio a las variables de entrada.
Función Objetivo
Es la parte del problema que queremos maximizar o minimizar. Por ejemplo, si queremos maximizar las ganancias, la función objetivo representará esas ganancias en términos de las variables del problema.
Solución Óptima
La "solución óptima" es el mejor resultado posible que se puede obtener, cumpliendo con todas las condiciones del problema. Gráficamente, en un problema de dos variables, esta solución se encuentra en una de las "esquinas" del poliedro de soluciones posibles.
- Solución óptima múltiple: A veces, un problema puede tener más de una solución óptima. Esto significa que hay varias combinaciones de variables que dan el mismo mejor resultado.
Algoritmo del Método Símplex: Pasos Sencillos
El algoritmo símplex es un proceso que se repite varias veces. Imagina que estás en una esquina de un poliedro y quieres llegar a la esquina más alta (o más baja). El algoritmo te guía paso a paso:
- Paso 1: Empezar en un punto de partida. El algoritmo comienza en una solución inicial, que suele ser el "origen" (donde todas las variables son cero), o un punto fácil de calcular.
- Paso 2: Decidir qué variable "entra". Se busca una variable que, si se le da un valor, pueda mejorar el resultado de la función objetivo (por ejemplo, aumentar las ganancias). Si no se puede mejorar más, ¡ya se encontró la solución óptima! Si sí se puede, se pasa al siguiente paso.
- Paso 3: Decidir qué variable "sale". Para que la nueva variable pueda entrar, otra variable debe salir (hacerse cero) para mantener el equilibrio del sistema. Se elige la que menos afecte negativamente las condiciones.
- Paso 4: Calcular la nueva solución. Se actualizan los valores de todas las variables, y se vuelve al Paso 2 para ver si se puede mejorar aún más.
Este proceso se repite hasta que el algoritmo no puede encontrar ninguna variable que mejore la función objetivo. En ese momento, se ha llegado a la solución óptima.
Galería de imágenes
Véase también
 En inglés: Simplex algorithm Facts for Kids
En inglés: Simplex algorithm Facts for Kids