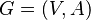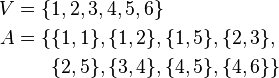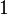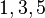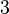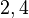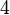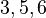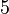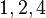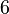Teoría de grafos para niños

Los grafos son el objeto de estudio de esta rama de la matemática. Arriba el grafo pez, en medio el grafo arco y abajo el grafo dodecaedro.

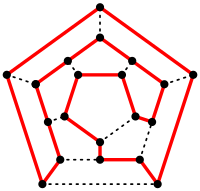
La teoría de grafos es una parte de las matemáticas que estudia los grafos. Los grafos son como dibujos formados por puntos y líneas que los unen. Esta teoría se usa mucho en las ciencias de la computación y en otras áreas.

Un grafo se representa con la letra G y tiene dos partes principales:

• Vértices (V): Son los puntos o "nodos" del grafo.
• Aristas (E): Son las líneas que conectan esos vértices.

Si una arista une dos vértices, decimos que esos vértices son "adyacentes". Si las líneas tienen una dirección (como flechas), el grafo se llama dígrafo.

La teoría de grafos se basa en la matemática discreta y usa ideas de otras áreas como la combinatoria, el álgebra y la geometría. Hoy en día, es muy importante en la informática y las telecomunicaciones, ayudando a optimizar rutas, procesos y búsquedas.

Historia de los Grafos: ¿Cómo Empezó Todo?

Los 7 puentes del río Pregel en Königsberg.

La historia de la teoría de grafos comenzó en el siglo XVIII con un famoso desafío: el problema de los puentes de Königsberg. En la ciudad de Königsberg (hoy Kaliningrado), había siete puentes sobre el Río Pregolya. El reto era encontrar un camino que cruzara cada puente una sola vez y regresara al punto de partida.

En 1736, el matemático Leonhard Euler resolvió este problema. Su trabajo es considerado el primer paso en la teoría de grafos. También mostró la conexión entre los grafos y la topología, que estudia las propiedades de las formas que no cambian al estirarse o doblarse.

Primeras Aplicaciones y Desafíos

En 1847, Gustav Kirchhoff usó los grafos para analizar redes eléctricas. Sus "leyes de Kirchhoff" ayudaron a calcular el voltaje y la corriente en los circuitos, siendo la primera vez que los grafos se aplicaron a un problema de ingeniería.

En 1852, Francis Guthrie propuso el Teorema de los cuatro colores. Este problema decía que cualquier mapa de países se podía colorear con solo cuatro colores, de modo que dos países vecinos nunca tuvieran el mismo color. Este desafío no se resolvió hasta 1976 por Kenneth Appel y Wolfgang Haken, y su búsqueda de solución ayudó a definir muchos conceptos clave de los grafos.

Arthur Cayley en 1857 usó grafos para estudiar los isómeros, que son compuestos químicos con la misma fórmula química pero diferente estructura molecular. Representó cada compuesto como un grafo tipo árbol, donde los vértices eran átomos y las aristas, los enlaces químicos.

El término "grafo" viene de la expresión inglesa graphic notation (notación gráfica), usada por primera vez por Edward Frankland y adoptada por Alexander Crum Brown en 1884. El primer libro sobre teoría de grafos lo escribió Dénes Kőnig en 1936.

¿Qué Partes Forman un Grafo?

Un grafo se compone de:

• Aristas: Son las líneas que conectan los vértices.
  • Aristas adyacentes: Son dos aristas que se encuentran en el mismo vértice.
  • Aristas paralelas: Son dos aristas que unen los mismos dos vértices.
  • Aristas cíclicas: Son aristas que empiezan y terminan en el mismo vértice.
  • Cruce: Es el punto donde dos aristas se cruzan.

• Vértices: También llamados "nodos", son los puntos del grafo. Cada vértice tiene una "valencia" o "grado", que es la cantidad de aristas que llegan a él.

• Camino: Es una secuencia de vértices conectados por aristas. Si hay un camino entre dos vértices, decimos que están conectados.

Tipos de Grafos: ¿Cuáles Existen?

Existen diferentes tipos de grafos, cada uno con características especiales:

• Grafo simple: Es el tipo más básico. Solo permite una arista entre dos vértices.
• Multigrafo o pseudografo: Permite más de una arista entre dos vértices, o aristas que se conectan a sí mismas (lazos).
• Grafo dirigido: Sus aristas tienen una dirección, como flechas.
• Grafo etiquetado: Las aristas o vértices tienen un valor o "peso" (generalmente un número).
• Grafo aleatorio: Sus aristas se forman con cierta probabilidad.
• Hipergrafo: Las aristas pueden conectar más de dos vértices a la vez.
• Grafo infinito: Tiene una cantidad ilimitada de vértices y aristas.
• Grafo plano: Se puede dibujar en una superficie plana sin que sus aristas se crucen. El Teorema de Kuratowski ayuda a saber si un grafo es plano.
• Grafo regular: Todos sus vértices tienen el mismo número de aristas conectadas.
• Grafo dual: Es un grafo que se crea a partir de otro grafo plano, donde cada región del grafo original se convierte en un vértice.

¿Cómo se Representan los Grafos?

Los grafos se pueden representar de varias maneras, tanto visualmente como para guardarlos en una computadora. La forma de guardarlos depende de cómo se usará el grafo. Las más comunes son las listas y las matrices.

Representación con Listas

• Lista de incidencia: Las aristas se guardan como pares de vértices que están conectados.
• Lista de adyacencia: Cada vértice tiene una lista de los vértices a los que está conectado.
• Lista de grados: Es una lista de números que muestra cuántas aristas tiene cada vértice.

Representación con Matrices

• Matriz de adyacencia: Es una tabla donde se marca con un 1 si hay una arista entre dos vértices y con un 0 si no la hay.
• Matriz de incidencia: Es una tabla que muestra qué aristas están conectadas a qué vértices.

Grafo	Conjuntos	Matriz de adyacencia	Matriz de incidencia	Secuencia de grados	Lista de adyacencia
				Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (4,3,2,3,3,1)	vértice lista de adyacencia

Problemas Famosos en Teoría de Grafos

Caminos y Ciclos Hamiltonianos

Ejemplo de un ciclo hamiltoniano.

Un ciclo es un recorrido que empieza y termina en el mismo vértice, sin pasar dos veces por la misma arista. Un ciclo hamiltoniano es un ciclo especial que además visita todos los vértices del grafo exactamente una vez (excepto el vértice de inicio/fin).

Imagina que estás en un museo muy grande y quieres recorrer todas las salas una sola vez. Esto sería buscar un ciclo hamiltoniano en el grafo del museo (las salas son vértices y los pasillos son aristas). Si no necesitas regresar al punto de partida, se llama camino hamiltoniano.

Encontrar estos ciclos o caminos es un problema difícil para las computadoras, especialmente en grafos grandes.

Grafos Planos: ¿Se Pueden Dibujar sin Cruces?

Un grafo es plano si se puede dibujar sin cruces de aristas. El problema de las tres casas y los tres pozos tiene solución sobre el toro, pero no en el plano.

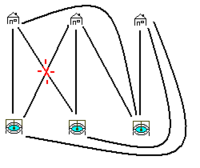
Un grafo es plano si puedes dibujarlo en una superficie plana sin que ninguna de sus aristas se cruce.

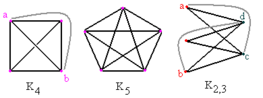
Un problema clásico es el de las "tres casas y los tres pozos": ¿Es posible conectar tres casas con tres pozos de agua sin que los caminos se crucen? La respuesta es no. Este problema se representa con un grafo bipartito completo llamado 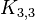, que no es plano.

Coloración de Grafos: El Problema de los Cuatro Colores

Mapa coloreado con 4-colores.

Grafo dual asociado al mapa con una 4-vértice coloración.

La coloración de grafos consiste en asignar un color a cada vértice de un grafo de manera que dos vértices conectados por una arista tengan colores diferentes. El objetivo es usar la menor cantidad de colores posible.

El famoso Teorema de los cuatro colores dice que cualquier mapa político (donde los países son de una sola pieza y el mundo es plano o esférico) puede colorearse con solo cuatro colores, de modo que los países vecinos tengan colores distintos. Este teorema fue muy difícil de demostrar y, de hecho, fue la primera vez que se usaron computadoras para ayudar a verificar una demostración matemática.

Características Importantes de los Grafos

Grafos Conexos: ¿Todo Está Unido?

Un grafo conexo (izquierda) y uno no conexo (derecha).

Un grafo conexo es aquel en el que puedes ir de cualquier vértice a cualquier otro vértice siguiendo un camino. Es como una red de carreteras donde puedes llegar a cualquier ciudad desde cualquier otra. Si un grafo no es conexo, significa que hay partes separadas.

Grafos Completos: ¡Todos Conectados!

Un grafo es completo si cada vértice está conectado directamente con todos los demás vértices. Es decir, hay una arista entre cada par posible de vértices. Un grafo completo con n vértices se escribe como 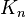y tiene exactamente 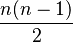aristas.

Grafos Bipartitos: Dos Grupos Separados

Un grafo es bipartito si sus vértices se pueden dividir en dos grupos, 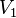y 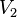, de tal manera que las aristas solo conectan vértices de un grupo con vértices del otro. No hay aristas que conecten vértices dentro del mismo grupo.

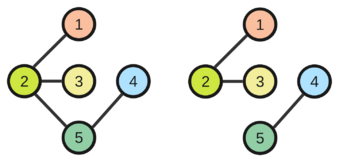
Árboles: Grafos sin Ciclos

Ejemplo de árbol.

Un grafo que no tiene ciclos (no puedes volver al mismo punto sin repetir aristas) y que conecta todos sus vértices se llama árbol. En un grafo con n vértices, un árbol siempre tiene exactamente n - 1 aristas. Los árboles son importantes porque conectan todos los vértices usando la menor cantidad de aristas posible. Se usan, por ejemplo, para estudiar cómo se relacionan las especies o las lenguas.

Grafos Ponderados o Etiquetados: Con Valores en las Aristas

En un grafo ponderado, cada arista tiene un número asociado, que puede representar una distancia, un costo o un tiempo. Por ejemplo, si las ciudades son vértices y las carreteras son aristas, el peso de la arista podría ser la distancia entre las ciudades. Esto ayuda a encontrar el camino más corto o más barato.

Diámetro de un Grafo: La Distancia Más Larga

En la figura se nota que K₄ es plano (desviando la arista ab al exterior del cuadrado), que K₅ no lo es, y que K₃,₂ lo es también (desvíos en gris).

La distancia entre dos vértices en un grafo es el número más pequeño de aristas que necesitas recorrer para ir de uno a otro. El diámetro de un grafo es la distancia más grande que puedes encontrar entre cualquier par de vértices.

Un ejemplo famoso es la hipótesis de los "seis grados de separación", que sugiere que cualquier persona en el mundo está conectada a cualquier otra a través de una cadena de no más de seis conocidos.

Aplicaciones de la Teoría de Grafos

La teoría de grafos es muy útil en muchas áreas:

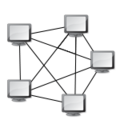
• Redes Sociales: Ayuda a entender cómo se conectan las personas en las redes sociales.
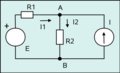
• Ingeniería: Se usa para diseñar circuitos electrónicos, sistemas de apertura y redes de computadoras.
• Transporte: Modela rutas de autobuses o trenes para encontrar los caminos más eficientes, usando algoritmos como el de Floyd.
• Administración de Proyectos: Técnicas como PERT usan grafos para planificar y optimizar los tiempos de los proyectos.
• Informática: Es fundamental para crear algoritmos complejos. El Algoritmo de Dijkstra, por ejemplo, encuentra el camino más corto en un grafo con pesos. El Algoritmo de Kruskal ayuda a encontrar la forma más barata de conectar todos los vértices.
• Biología: Los grafos pueden representar hábitats y senderos de animales, ayudando a los científicos a entender cómo se mueven las especies.

Algoritmos Importantes de Grafos

Algunos de los algoritmos más conocidos que usan grafos son:

• Algoritmo de búsqueda en anchura (BFS)
• Algoritmo de búsqueda en profundidad (DFS)
• Algoritmo de Dijkstra (para encontrar el camino más corto)
• Algoritmo de Kruskal (para encontrar el árbol de expansión mínima)
• Algoritmo de Floyd-Warshall (para encontrar los caminos más cortos entre todos los pares de vértices)

Galería de imágenes

• 

  Mapas conceptuales

• 

  Plano de estaciones del metro.

• 

  Plano de autopistas.

• 

  Circuito eléctrico

• 

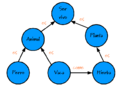
  Sociograma de una red social

• 

  Topología de red de computadores

• 

  Organigramas

• 

  Isomeros

• 

  Arquitectura de redes de telefonía móvil

• 

  Draws de eliminación directa (ej: tenis)

Véase también

En inglés: Graph theory Facts for Kids

• Grafo
• Anexo:Galería de grafos
• Teóricos de grafos
• Teorema de König (teoría de grafos)
• Álgebra de grafos