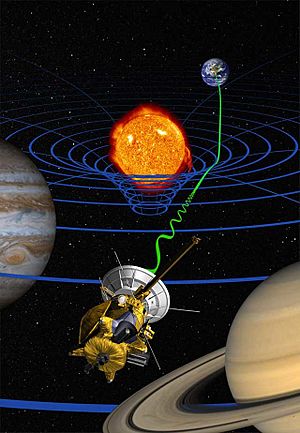
Relatividad general para niños

Para una presentación accesible y menos técnica, véase Introducción a la relatividad general.

Representación artística de la explosión de la supernova SN 2006gy, situada a 238 millones de años luz. De ser válido el principio de acción a distancia, las perturbaciones de origen gravitatorio de este estallido nos afectarían inmediatamente, más tarde nos llegarían las de origen electromagnético, que se transmiten a la velocidad de la luz.

Esquema bidimensional de la curvatura del espacio-tiempo (cuatro dimensiones) generada por una masa esférica.

La teoría general de la relatividad o relatividad general es una teoría del campo gravitatorio y de los sistemas de referencia generales, publicada por Albert Einstein en 1915 y 1916.

El nombre de la teoría se debe a que generaliza la llamada teoría especial de la relatividad y el principio de relatividad para un observador arbitrario. Los principios fundamentales introducidos en esta generalización son el principio de equivalencia, que describe la aceleración y la gravedad como aspectos distintos de la misma realidad, la noción de la curvatura del espacio-tiempo y el principio de covariancia generalizado. La teoría de la relatividad general propone que la propia geometría del espacio-tiempo se ve afectada por la presencia de materia, de lo cual resulta una teoría relativista del campo gravitatorio. De hecho la teoría de la relatividad general predice que el espacio-tiempo no será plano en presencia de materia y que la curvatura del espacio-tiempo será percibida como un campo gravitatorio.

La intuición básica de Einstein fue postular que en un punto concreto no se puede distinguir experimentalmente entre un cuerpo acelerado uniformemente y un campo gravitatorio uniforme. La teoría general de la relatividad permitió también reformular el campo de la cosmología.

Einstein expresó el propósito de la teoría de la relatividad general para aplicar plenamente el programa de Ernst Mach de la relativización de todos los efectos de inercia, incluso añadiendo la llamada constante cosmológica a sus ecuaciones de campo para este propósito. Este punto de contacto real de la influencia de Ernst Mach fue claramente identificado en 1918, cuando Einstein distingue lo que él bautizó como el principio de Mach (los efectos inerciales se derivan de la interacción de los cuerpos) del principio de la relatividad general, que se interpreta ahora como el principio de covariancia general.

El matemático alemán David Hilbert escribió e hizo públicas las ecuaciones de la covariancia antes que Einstein, ello resultó en no pocas acusaciones de plagio contra Einstein, pero probablemente sea más porque es una teoría (o perspectiva) geométrica. La misma postula que la presencia de masa o energía «curva» el espacio-tiempo, y esta curvatura afecta la trayectoria de los cuerpos móviles e incluso la trayectoria de la luz.

Contenido

Historia
Antecedentes
Principios generales
Los diferentes tensores y escalares de la relatividad general
Soluciones de las ecuaciones de campo de Einstein
Predicciones de la relatividad general
Aplicaciones prácticas
Relación con otras teorías físicas
Transición de la relatividad especial a la relatividad general
Véase también

Historia

Poco después de la formulación de la teoría de la relatividad especial en 1905, Albert Einstein comenzó a elucubrar cómo describir los fenómenos gravitatorios con ayuda de la nueva mecánica. En 1907 se embarcó en la búsqueda de una nueva teoría relativista de la gravedad que duraría ocho años. Después de numerosos desvíos y falsos comienzos, su trabajo culminó el 25 de noviembre de 1915 con la presentación a la Academia Prusiana de las Ciencias de su artículo, que contenía las que hoy son conocidas como "Ecuaciones de Campo de Einstein". Estas ecuaciones forman el núcleo de la teoría y especifican cómo la densidad local de materia y energía determina la geometría del espacio-tiempo.

Las ecuaciones de campo de Einstein son no lineales y muy difíciles de resolver. Einstein utilizó los métodos de aproximación en la elaboración de las predicciones iniciales de la teoría. Pero ya en 1916, el astrofísico Karl Schwarzschild encontró la primera solución exacta no trivial de las Ecuaciones de Campo de Einstein, la llamada Métrica de Schwarzschild. Esta solución sentó las bases para la descripción de las etapas finales de un colapso gravitacional, y los objetos que hoy conocemos como agujeros negros. En el mismo año, se iniciaron los primeros pasos hacia la generalización de la solución de Schwarzschild a los objetos con carga eléctrica, obteniéndose así la solución de Reissner-Nordström, ahora asociada con la carga eléctrica de los agujeros negros.

En 1917, Einstein aplicó su teoría al universo en su conjunto, iniciando el campo de la cosmología relativista. En línea con el pensamiento contemporáneo, en el que se suponía que el universo era estático, agregó a sus ecuaciones una constante cosmológica para reproducir esa "observación". En 1929, sin embargo, el trabajo de Hubble y otros demostraron que nuestro universo se está expandiendo. Esto es fácilmente descrito por las soluciones encontradas por Friedmann en 1922 para la expansión cosmológica, que no requieren de una constante cosmológica. Lemaître utilizó estas soluciones para formular la primera versión de los modelos del Big Bang, en la que nuestro universo ha evolucionado desde un estado anterior extremadamente caliente y denso. Einstein declaró más tarde que agregar esa constante cosmológica a sus ecuaciones fue el mayor error de su vida.

Durante ese período, la relatividad general se mantuvo como una especie de curiosidad entre las teorías físicas. Fue claramente superior a la gravedad newtoniana, siendo consistente con la relatividad especial y contestaba varios efectos no explicados por la teoría newtoniana. El mismo Einstein había demostrado en 1915 cómo su teoría lograba explicar el avance del perihelio anómalo del planeta Mercurio sin ningún parámetro arbitrario. Del mismo modo, en una expedición de 1919 liderada por Eddington confirmaron la predicción de la relatividad general para la desviación de la luz estelar por el Sol durante el eclipse total de Sol del 29 de mayo de 1919, haciendo famoso a Einstein instantáneamente. Sin embargo, esta teoría ha entrado en la corriente de la física teórica y la astrofísica desarrolladas aproximadamente entre 1960 y 1975, ahora conocido como la edad de oro de la relatividad general. Los físicos empezaron a comprender el concepto de agujero negro, y a identificar la manifestación de objetos astrofísicos como los cuásares. Cada vez más precisas, las pruebas del sistema solar confirmaron el poder predictivo de la teoría, y la cosmología relativista, también se volvió susceptible a encaminar pruebas observacionales.

Antecedentes

Los éxitos explicativos de la teoría de la relatividad especial condujeron a la aceptación de la teoría prácticamente por la totalidad de los físicos. Eso llevó a que antes de la formulación de la relatividad general existieran dos teorías físicas incompatibles:

La teoría especial de la relatividad, covariante en el sentido de Lorentz, que integraba adecuadamente el electromagnetismo, y que descarta explícitamente las acciones instantáneas a distancia.
La teoría de la gravitación de Newton, explícitamente no-covariante, que explicaba de manera adecuada la gravedad mediante acciones instantáneas a distancia (concepto de fuerza a distancia).

La necesidad de buscar una teoría que integrase, como casos límites particulares, las dos anteriores requería la búsqueda de una teoría de la gravedad que fuese compatible con los nuevos principios relativistas introducidos por Einstein. Además de incluir la gravitación en una teoría de formulación covariante, hubo otra razón adicional. Einstein había concebido la teoría especial de la relatividad como una teoría aplicable solo a sistemas de referencia inerciales, aunque realmente puede generalizarse a sistemas acelerados sin necesidad de introducir todo el aparato de la relatividad general. La insatisfacción de Einstein con su creencia de que la teoría era aplicable solo a sistemas inerciales le llevó a buscar una teoría que proporcionara descripciones físicas adecuadas para un sistema de referencia totalmente general.

Esta búsqueda era necesaria, ya que según la relatividad espacial ninguna información puede viajar a mayor velocidad que la luz, y por lo tanto no puede existir relación de causalidad entre dos eventos unidos por un intervalo de tipo espacio (space-like). Sin embargo, uno de los pilares fundamentales de la gravedad newtoniana, el principio de acción a distancia, supone que las alteraciones producidas en el campo gravitatorio se transmiten instantáneamente a través del espacio. La contradicción entre ambas teorías es evidente, puesto que asumir las tesis de Newton llevaría implícita la posibilidad de que un observador fuera afectado por las perturbaciones gravitatorias producidas fuera de su cono de luz.

Einstein resolvió este problema interpretando los fenómenos gravitatorios como simples alteraciones de la curvatura del espacio-tiempo producidas por la presencia de masas. De ello se deduce que el campo gravitatorio, al igual que el campo electromagnético, tiene una entidad física independiente y sus variaciones se transmiten a una velocidad finita en forma de ondas gravitacionales. La presencia de masa, energía o momentum en una determinada región de la variedad tetradimensional, provoca la alteración de los coeficientes de la métrica, en una forma cuyos detalles pormenorizados analizaremos en las secciones siguientes.

En esta visión, la gravitación solo sería una pseudo-fuerza (equivalente a la fuerza de Coriolis, o a la fuerza centrífuga) efecto de haber escogido un sistema de referencia no-inercial.

Principios generales

Las características esenciales de la teoría de la relatividad general son las siguientes:

El principio general de covariancia: las leyes de la Física deben tomar la misma forma matemática en todos los sistemas de coordenadas.
El principio de equivalencia o de invariancia local de Lorentz: las leyes de la relatividad especial (espacio plano de Minkowski) se aplican localmente para todos los observadores inerciales.
La curvatura del espacio-tiempo es lo que observamos como un campo gravitatorio, en presencia de materia la geometría del espacio-tiempo no es plana sino curva, una partícula en movimiento libre inercial en el seno de un campo gravitatorio sigue una trayectoria geodésica.

Principio de covariancia

Artículo principal: Principio de covariancia

El principio de covariancia es la generalización de la teoría de la relatividad especial, donde se busca que las leyes físicas tengan la misma forma en todos los sistemas de referencia. Esto último equivale a que todos los sistemas de referencia sean indistinguibles, y desde el punto de vista físico equivalentes. En otras palabras, que cualquiera que sea el movimiento de los observadores, las ecuaciones tendrán la misma forma matemática y contendrán los mismos términos. Ésta fue la principal motivación de Einstein para que estudiara y postulara la relatividad general.

El principio de covariancia sugería que las leyes debían escribirse en términos de tensores, cuyas leyes de transformación covariantes y contravariantes podían proporcionar la "invarianza" de forma buscada, satisfaciéndose el principio físico de covariancia.

El principio de equivalencia

Los dos astronautas de la imagen se encuentran en una nave en caída libre. Por ello no experimentan gravedad alguna (su estado se describe coloquialmente como de «gravedad cero»). Se dice por ello que son observadores inerciales.

Un hito fundamental en el desarrollo de la teoría de la relatividad general lo constituye el principio de equivalencia, enunciado por Albert Einstein en el año 1912 y al que su autor calificó como «la idea más feliz de mi vida». Dicho principio supone que un sistema que se encuentra en caída libre y otro que se mueve en una región del espacio-tiempo sin gravedad se encuentran en un estado físico similar: en ambos casos se trata de sistemas inerciales.

Galileo distinguía entre cuerpos de movimiento inercial (en reposo o moviéndose a velocidad constante) y cuerpos de movimiento no inercial (sometidos a un movimiento acelerado). En virtud de la segunda ley de Newton (que se remonta a los trabajos del dominico español Domingo de Soto), toda aceleración estaba causada por la aplicación de una fuerza exterior. La relación entre fuerza y aceleración se expresaba mediante esta fórmula:

$m = \frac{F}{a}$

donde a es la aceleración, F la fuerza y m la masa. La fuerza podía ser de origen mecánico, electromagnético o, cómo no, gravitatorio. Según los cálculos de Galileo, la aceleración gravitatoria de los cuerpos era constante y equivalía a 9,8 m/s² sobre la superficie terrestre. La fuerza con la que un cuerpo era atraído hacia el centro de la Tierra se denominaba peso. Evidentemente, según los principios de la mecánica clásica un cuerpo en caída libre no es un sistema inercial, puesto que se mueve aceleradamente dentro del campo gravitatorio en que se encuentra.

Sin embargo, la teoría de la relatividad considera que los efectos gravitatorios no son creados por fuerza alguna, sino que encuentran su causa en la curvatura del espacio-tiempo generada por la presencia de materia. Por ello, un cuerpo en caída libre es un sistema (localmente) inercial, ya que no está sometido a ninguna fuerza (porque la gravedad tiene este carácter en relatividad general). Un observador situado en un sistema inercial (como una nave en órbita) no experimenta ninguna aceleración y es incapaz de discernir si está atravesando o no, un campo gravitatorio. Como consecuencia de ello, las leyes de la física se comportan como si no existiera curvatura gravitatoria alguna. De ahí que el principio de equivalencia también reciba el nombre de Invariancia Local de Lorentz: En los sistemas inerciales rigen los principios y axiomas de la relatividad especial.

El principio de equivalencia implica asimismo que los observadores situados en reposo sobre la superficie de la Tierra no son sistemas inerciales (experimentan una aceleración de origen gravitatorio de unos 9,8 metros por segundo al cuadrado, es decir, "sienten su peso").

**Ejemplos de sistemas inerciales según el Principio de Equivalencia**
Sistema	¿Es inercial? (Principio de Equivalencia)	¿Es inercial? (Mecánica newtoniana)
Cuerpo en caída libre	Sí	No
Cuerpo en reposo sobre la superficie terrestre	No	Sí
Planeta orbitando alrededor del sol	Sí	No
Nave precipitándose hacia la tierra	Sí	No
Cohete despegando desde una base de lanzamiento	No	No

Aunque la mecánica clásica tiene en cuenta la aceleración medida por un observador en reposo respecto al campo gravitatorio (p. ej. un astrónomo); el Principio de Equivalencia, contrariamente, toma en consideración la aceleración experimentada por un observador situado en el sistema en cuestión: cualquier cuerpo que se mueva sin restricciones por un campo gravitatorio puede ser considerado como un sistema inercial. Es el caso de los planetas que orbitan en torno del Sol y de los satélites que orbitan alrededor de los primeros: los habitantes de la Tierra no llegan a percibir si nos estamos acercando o alejando del Sol, ni si nos encontramos en el afelio o en el perihelio, a pesar de las enormes diferencias de la gravedad solar.

La gravedad se convierte, en virtud del Principio de Equivalencia, en una fuerza aparente, como la fuerza centrífuga y la fuerza de Coriolis: en estos dos últimos supuestos su aparición es debida a la elección de un marco de referencia acelerado (un observador situado en la superficie de una esfera en rotación). En el caso de la gravedad, únicamente percibimos la fuerza aparente gravitatoria cuando escogemos un sistema de referencia no inercial (en reposo sobre la superficie terrestre), pero no cuando nos situamos en otro que sí lo es (un cuerpo en caída libre).

Aunque el principio de equivalencia fue históricamente importante en el desarrollo de la teoría, no es un ingrediente necesario de una teoría de la gravedad, como prueba el hecho de que otras teorías métricas de la gravedad, como la teoría relativista de la gravitación prescindan del principio de equivalencia. Además conviene señalar que el principio de equivalencia no se cumple en presencia de campos electromagnéticos, por ejemplo una partícula cargada moviéndose a lo largo de una geodésica de un espacio-tiempo cualquiera en general emitirá radiación, a diferencia de una partícula cargada moviéndose a lo largo de una geodésica del espacio de Minkowski. Ese y otros hechos sugieren que el principio de equivalencia a pesar de su equivalencia histórica no es parte esencial de una teoría relativista de la gravitación.

La curvatura del espacio-tiempo

Artículo principal: Curvatura del espacio-tiempo

La aceptación del principio de equivalencia por Albert Einstein le llevó a un descubrimiento ulterior: la contracción o curvatura del tiempo como consecuencia de la presencia de un campo gravitatorio, que quedó expresado en su artículo de 1911 "Sobre la influencia de la gravedad en la propagación de la luz".

Supongamos que un fotón emitido por una estrella cercana se aproxima a la Tierra. En virtud de la ley de conservación del tetramomentum la energía conservada del fotón permanece invariante. Por otro lado, el principio de equivalencia implica que un observador situado en el fotón (que es un sistema inercial, es decir, se halla en caída libre) no experimenta ninguno de los efectos originados por el campo gravitatorio terrestre. De ello se deduce que la energía conservada del fotón no se altera como consecuencia de la acción de la gravedad, y tampoco lo hace la frecuencia de la luz, ya que, según la conocida fórmula de la física cuántica, la energía de un fotón es igual a su frecuencia v multiplicada por la constante de Planck h: E = hν.

En la imagen se reproduce el corrimiento gravitacional hacia el rojo de un fotón que escapa del campo gravitatorio solar y se dirige hacia la Tierra. En este caso, la onda electromagnética pierde progresivamente energía y su frecuencia disminuye conforme aumenta la distancia al Sol.

Ahora bien, si las observaciones las realizara un astrónomo situado en la superficie de la Tierra, esto es, en reposo respecto su campo gravitatorio, los resultados serían muy diferentes: el astrónomo podría comprobar cómo el fotón, por efecto de su caída hacia la Tierra, va absorbiendo progresivamente energía potencial gravitatoria y, como consecuencia de esto último, su frecuencia se corre hacia el azul. Los fenómenos de absorción de energía por los fotones en caída libre y corrimiento hacia el azul se expresan matemáticamente mediante las siguientes ecuaciones:

\ E_{obs}=E_{con} e^{-\Phi}

\ h \nu_{rec}=h \nu_{em} e^{-\Phi}

\nu_{rec}=\nu_{em} e^{-\Phi}\,

donde $E_{obs}\,$ es la energía medida por un observador en reposo respecto al campo gravitatorio (en este caso un astrónomo), $\ \Phi$ el potencial gravitatorio de la región donde se encuentra este, $\ E_{con}$ la energía conservada del fotón, $\nu_{em}$ la frecuencia de emisión, $\nu_{rec}$ es la frecuencia percibida por el observador (y corrida hacia el azul) y $\ h$ la constante de Planck.

Ahora bien, en el párrafo anterior hemos demostrado que la energía conservada del fotón permanece invariante. Por tanto, ¿cómo es posible que exista esta divergencia entre los resultados de la medición de la energía obtenidos por el astrónomo ( $E_{obs}$ ) y la energía conservada del fotón ( $E_{con}$ )? La única manera de resolver esta contradicción es considerando que el tiempo se ralentiza como consecuencia de la presencia de un campo gravitatorio. De este modo, la citada ecuación:

$\ \nu_{rec}=\nu_{em} e^{-\Phi}$

puede escribirse de este modo:

$\ \frac{\mbox{ciclos}}{\Delta t_{obs}}= \frac{\mbox{ciclos}}{\Delta t_{em}} e^{-\Phi}$

Es decir, la frecuencia es igual al número de ciclos que tienen lugar en un determinado período (generalmente, un segundo). Donde $\Delta t_{em}$ es el tiempo medido por un observador situado a una distancia infinita del cuerpo masivo (y por lo tanto no experimenta la atracción gravitatoria de este), mientras que $\Delta t_{obs}$ es el tiempo medido por un observador bajo la influencia del campo gravitatorio y en reposo respecto a este (como, por ejemplo, una persona situada sobre la superficie terrestre). De ahí se deduce que cerca de un cuerpo masivo el tiempo se ralentiza, siguiendo estas reglas matemáticas:

\Delta t_{em} = \Delta t_{obs} e^{-\Phi}\,

\Delta t_{obs} = \Delta t_{em} e^{\Phi}\,

En una singularidad espacio-temporal (como las que existen en el interior de los agujeros negros), la densidad de masa-materia y el campo gravitatorio tienden al infinito, lo que provoca la congelación del tiempo y por lo tanto la eliminación de todo tipo de procesos dinámicos:

$\lim_{r\to 0} \Delta t_{obs}= \Delta t_{em} e^{-\infty} \to \lim_{r\to 0} \Delta t_{obs}= 0$

En la imagen, dos partículas en reposo relativo, en un espacio-tiempo llano

Se representan en este esquema dos partículas que se acercan entre sí siguiendo un movimiento acelerado. La interpretación newtoniana supone que el espacio-tiempo es llano y que lo que provoca la curvatura de las líneas de universo es la fuerza de interacción gravitatoria entre ambas partículas. Por el contrario, la interpretación einsteiniana supone que las líneas de universo de estas partículas son geodésicas ("rectas"), y que es la propia curvatura del espacio tiempo lo que provoca su aproximación progresiva.

La contracción del tiempo debido a la presencia de un campo gravitatorio fue confirmada experimentalmente en el año 1959 por el experimento Pound-Rebka-Snider, llevado a cabo en la universidad de Harvard. Se colocaron detectores electromagnéticos a una cierta altura y se procedió a emitir radiación desde el suelo. Todas las mediciones que se realizaron confirmaron que los fotones habían experimentado un corrimiento hacia el rojo durante su ascenso a través del campo gravitatorio terrestre.

Hoy en día, el fenómeno de la contracción del tiempo tiene cierta importancia en el marco del servicio localizador GPS, cuyas exigencias de exactitud requieren de una precisión extrema: Basta con que se produzca un retraso de 0.04 microsegundos en la señal para que se produzca un error de posicionamiento de unos 10 metros. De ahí que las ecuaciones de Einstein hayan de ser tenidas en cuenta al calcular la situación exacta de un determinado objeto sobre la superficie terrestre.

Desde un punto de vista teórico, el artículo de Einstein de 1911 tuvo una importancia aún mayor. Pues, la contracción del tiempo conllevaba también, en virtud de los principios de la relatividad especial, la contracción del espacio. De ahí que fuera inevitable a partir de este momento descartar la existencia de un espacio-tiempo llano, y fuera necesario asumir la curvatura de la variedad espacio-temporal como consecuencia de la presencia de masas.

En la relatividad general, fenómenos que la mecánica clásica atribuye a la acción de la fuerza de gravedad, tales como una caída libre, la órbita de un planeta o la trayectoria de una nave espacial, son interpretados como efectos geométricos del movimiento en un espacio-tiempo curvado. De hecho una partícula libre en un campo gravitatorio sigue líneas de curvatura mínima a través de este espacio tiempo-curvado.

Finalmente, podemos hacer referencia a la desviación de los rayos de la luz como consecuencia de la presencia de un cuerpo masivo, fenómeno que da lugar a efectos ópticos como las lentes gravitacionales o los anillos de Einstein.

Frente de onda desviado. Lente gravitacional. Experimento de Eddington.

Formulación matemática y consideraciones generales

Artículo principal: Introducción matemática a la relatividad general

No te preocupes por tus problemas con las matemáticas; te aseguro que los míos son mucho mayores.

A. Einstein, en una carta a una niña de nueve años.

Matemáticamente, Einstein conjeturó que la geometría del universo deja de ser euclidiana por la presencia de masas. Einstein modelizó que el universo era un tipo de espacio-tiempo curvo mediante una variedad pseudoriemanniana y sus ecuaciones de campo establecen que la curvatura seccional de esta variedad en un punto está relacionada directamente con el tensor de energía-momento en dicho punto.

Dicho tensor es una medida de la densidad de materia y energía. La curvatura "le dice a la materia como moverse", y de forma recíproca la "materia le dice al espacio como curvarse". En términos más precisos las trayectorias de las partículas se ven afectadas por la curvatura, y la presencia de muchas partículas en una región altera notoriamente la curvatura. La relatividad general se distingue de otras teorías alternativas de la gravedad por la simplicidad de acoplamiento entre materia y curvatura.

Aunque todavía no existe una teoría cuántica de la gravedad que incorpore tanto a la mecánica cuántica como a la teoría de la relatividad general y que proponga una ecuación de campo gravitatorio que sustituya a la de Einstein, pocos físicos dudan que una teoría cuántica de la gravedad pondrá a la relatividad general en el límite apropiado, así como la relatividad general predice la ley de la gravedad en el límite no relativista.

Los diferentes tensores y escalares de la relatividad general

Artículo principal: Introducción matemática a la relatividad general

La derivada covariante

Los cuerpos en caída libre (como las naves en órbita) son sistemas inerciales en los que la derivada covariante de su velocidad es nula (

\nabla_{\vec u} u^r = 0

). Por ello, no experimentan ningún tipo de aceleración inercial provocada por la "fuerza gravitatoria". Sin embargo, un observador externo, como un astrónomo situado en la Tierra, puede observar cómo dicho cuerpo en caída libre se aproxima a la Tierra con una aceleración creciente (de ahí que la derivada ordinaria de la velocidad en este caso sea diferente a cero —

\frac{d v^r}{dt} \not= 0

—)

Dice la leyenda apócrifa que fue la manzana de un árbol la que provocó que Newton se diera cuenta que los objetos caen y por lo tanto aceleran como consecuencia de la gravitación universal. Y es que los objetos en reposo sobre la superficie terrestre experimentan, como consecuencia de la fuerza aparente gravitatoria, una aceleración inercial de

9,8 \text{ m/s}^2

(y por lo tanto la derivada covariante de su velocidad también tiene ese valor

\nabla_{\vec u} u^r = 9,8

). Sin embargo, dichos objetos, puesto que están en reposo, tienen una aceleración relativa nula respecto a un observador terrestre (es decir, la derivada ordinaria de su velocidad es cero (

\frac{d v^r}{dt} = 0

)

Uno de los conceptos esenciales sobre el que gira toda la teoría de la relatividad general es el de derivada covariante (a veces impropiamente llamada conexión afín), que fue definida por primera vez por el matemático italiano Tullio Levi-Civita y que puede ser considerada tanto desde una perspectiva física como desde otra matemática.

Desde un punto de vista físico, la derivada ordinaria de la velocidad es la aceleración de un cuerpo medida por un observador externo en reposo respecto a un campo gravitatorio (por ejemplo, un astrónomo situado sobre la superficie terrestre). En este caso el observador se mantiene a una distancia r constante del centro de masas, pero no así el objeto observado, que si consideramos que está en caída libre, progresivamente se irá aproximando al origen del campo gravitatorio, y el observador externo detectará que tiene una aceleración constante g.

Por el contrario, la derivada covariante de la velocidad $\left(\frac{D \vec u}{d\tau}\right)$ o $\nabla_{\vec u} \vec u$ es la aceleración medida por un observador comóvil, es decir, que está en reposo respecto al cuerpo en caída libre (por ejemplo, el piloto de un avión en caída libre o los tripulantes de una nave espacial con sus motores apagados) y que a diferencia de la derivada ordinaria, no detectará ninguna aceleración, a menos que el piloto encienda los motores o que algún meteorito lo impacte.

En resumidas cuentas, la derivada ordinaria se utiliza para computar la aceleración ordinaria de un cuerpo, mientras que la derivada covariante es empleada para calcular su aceleración inercial. Según la mecánica galileana y newtoniana estos dos tipos de aceleración son idénticos, y sobre la base de este axioma se desarrollaron nuevos principios mecánicos como el Principio de d'Alembert. Sin embargo, del principio de equivalencia de Einstein se deduce que cuando un cuerpo está en caída libre tiene una aceleración ordinaria que depende de la masa del cuerpo sobre el cual está cayendo, pero su aceleración inercial es nula, a menos que se le aplique alguna otra fuerza. De ahí que para Einstein fuera absolutamente necesario introducir en su teoría el concepto de derivada covariante.

Desde un punto de vista estrictamente matemático, el cálculo de la derivada covariante tiene lugar a través de un sencillo procedimiento. Se procede en primer lugar al cómputo de la derivada parcial covariante y luego se generaliza ésta.

La derivada ordinaria se aplica exclusivamente sobre los componentes de un vector, mientras que la derivada covariante se aplica también sobre las bases del espacio vectorial, ya que la percepción del espacio-tiempo dependerá de la velocidad del observador comóvil:

\nabla_\beta \vec u = \partial_\beta (u^\alpha \vec e_\alpha)

Sobre esta ecuación procedemos a aplicar la regla del producto (o de Leibniz),

\nabla_\beta \vec u = (\partial_\beta u^\alpha) \vec e_\alpha + u^\alpha (\partial_\beta \vec e_\alpha)

Llegados a este punto introducimos una nueva notación, los símbolos de Christoffel, que pueden ser definidos como el componente $\ \mu$ de la derivada parcial de $\ e_\alpha$ respecto a $\ \beta$ : $\partial_\beta \vec e_\alpha = \Gamma^\mu_{\alpha\beta} \vec e_\mu$ . De este modo:

\nabla_\beta \vec u = (\partial_\beta u^\alpha) \vec e_\alpha + u^\alpha \Gamma^\mu_{\alpha\beta} \vec e_\mu

Realizamos un intercambio de índices ( $\ \mu$ por $\ \alpha$ ) en el último término del segundo miembro de la ecuación:

\nabla_\beta \vec u = (\partial_\beta u^\alpha) \vec e_\alpha + \Gamma^\alpha_{\mu\beta}u^\mu \vec e_\alpha

Y obtenemos con ello los componentes de la derivada parcial covariante de la velocidad, que equivalen a la expresión entre paréntesis:

\nabla_\beta \vec u = (\partial_\beta u^\alpha + \Gamma^\alpha_{\mu\beta}u^\mu) \vec e_\alpha

\nabla_\beta u^\alpha = \partial_\beta u^\alpha + \Gamma^\alpha_{\mu\beta}u^\mu

Generalizamos dichos componentes multiplicándolos por el componente $\ \beta$ de la tetravelocidad ( $\ u^\beta = \frac{dx^\beta}{d \tau}$ ) y obtenemos con ello la derivada covariante de la velocidad:

\frac{dx^\beta}{d \tau}\nabla_\beta u^\alpha = \partial_\beta u^\alpha \frac{dx^\beta}{d \tau} + \Gamma^\alpha_{\mu\beta}u^\mu \frac{dx^\beta}{d \tau}

\nabla_\vec u u^\alpha = \frac{du^\alpha}{d \tau} + \Gamma^\alpha_{\mu\beta}u^\mu u^\beta

Puesto que para un observador inercial (p. ej. un cuerpo en caída libre) $\nabla_\vec u u^a = 0$ , esta última ecuación toma la siguiente forma:

0 = \frac{du^\alpha}{d \tau} + \Gamma^\alpha_{\mu\beta}u^\mu u^\beta

\frac{du^\alpha}{d \tau} = - \Gamma^\alpha_{\mu\beta}u^\mu u^\beta

Estas fórmulas reciben el nombre de ecuación de las líneas geodésicas, y se utilizan para calcular la aceleración gravitatoria de cualquier cuerpo.

Con ayuda de la ecuación de las líneas geodésicas podemos determinar la aceleración radial y angular de la Tierra respecto al Sol. Puesto que la curvatura gravitatoria los valores de los símbolos de Christoffel aumentan conforme nos acercamos al Sol, de ello se deduce que la aceleración de la Tierra es máxima en las proximidades del perihelio, exactamente tal y como predicen las leyes de Newton y Kepler.

A los lectores principiantes puede chocarles la propia definición de los símbolos de Christoffel. A fin de cuentas, en el espacio euclídeo, la derivada de una base (por ejemplo $e_x$ ) respecto a otra coordenada (pongamos $y$ ) es siempre cero, por la simple razón de que las bases de ambas coordenadas son ortogonales. Sin embargo, esto no sucede así en las variedades curvas, como por ejemplo las superficies de un cilindro o de una esfera: En tales casos, los símbolos de Christoffel no son iguales a cero, sino que son funciones de las derivadas del tensor métrico. La relación matemática entre estas dos magnitudes matemáticas se expresa mediante la siguiente ecuación:

\ \Gamma^\alpha_{\beta\mu} = \frac{1}{2} g^{\alpha\sigma} (\partial_\mu g_{\sigma\beta} + \partial_\beta g_{\sigma\mu} - \partial_\sigma g_{\beta\mu})

Los símbolos de Christoffel constituyen el parámetro principal que determina cuán grande es el grado de curvatura existente en una región determinada y con su ayuda podemos conocer cuál va a ser la trayectoria de una geodésica en un espacio curvo. En el caso de la variedad espacio-temporal, la Teoría de la Relatividad afirma que la curvatura viene originada por la presencia de tetramomentum y por ello, cuanta mayor sea la densidad de materia existente en una determinada región, mayores serán los valores de los símbolos de Christoffel.

Los principios de general covariancia y de acoplamiento mínimo

Artículo principal: Principio de acoplamiento mínimo

En un espacio-tiempo curvo, las leyes de la física se modifican mediante el Principio de acoplamiento mínimo, que supone que las ecuaciones matemáticas en cuya virtud se expresan aquellas experimentan las siguientes modificaciones:

La derivada ordinaria es sustituida por la derivada covariante.
La métrica de Minkowski es sustituida por una formulación general del tensor métrico.

\eta _{\mu \nu} \longrightarrow g_{\mu \nu}\left ( x \right )

\partial_\mu \longrightarrow \nabla_\mu \left ( x \right )

De este modo, la ecuación galileana de los sistemas inerciales se transforma en virtud de dicho principio en la ecuación relativista de las líneas geodésicas:

\partial_\beta u^\alpha = 0 \to \nabla_\beta u^\alpha = 0

Ley de conservación de la energía:

\partial_\alpha T^{\alpha\beta} = 0 \to \nabla_\alpha T^{\alpha\beta} = 0

Sin embargo, en virtud del principio de simetría de los símbolos de Christoffel, las leyes electromagnéticas en general no experimentan modificaciones debidas a la curvatura gravitatoria:

F_{\alpha \beta} = \partial_\alpha A_\beta - \partial_\beta A_\alpha

F_{\alpha \beta} = \nabla_\alpha A_\beta - \nabla_\beta A_\alpha

F_{\alpha \beta} = \partial_\alpha A_\beta - \Gamma^\mu_{\beta\alpha}A_\mu -\partial_\beta A_\alpha + \Gamma^\mu_{\alpha\beta}A_\mu

\Gamma^\mu_{\alpha\beta} = \Gamma^\mu_{\beta\alpha}

**Alteración de las leyes físicas producida por la curvatura**
Objeto o ley físico-matemática	Espacio-tiempo llano	Espacio-tiempo curvo	¿Se produce alteración por la curvatura?
Ley de conservación de la energía	$\partial_\alpha T^{\alpha\beta} = 0$	$\nabla_\alpha T^{\alpha\beta} = 0$	Sí
Tensor electromagnético	$F_{ij} = \partial_i A_j - \partial_j A_i$	$F_{ij} = \nabla_i A_j - \nabla_j A_i = \partial_i A_j - \partial_j A_i$	No
Ecuaciones de Maxwell			No
Velocidad de la luz	$\ c$	$\ c$	No
Ecuación de un sistema inercial	$\frac{du^\alpha}{dt} = 0$	$\nabla_\vec u \vec u = \frac{du^\alpha}{dt} + \Gamma^\alpha_{\beta\nu}u^\beta u^\mu= 0$	Sí
Aceleración	$a=\frac{dx^2}{dt^2}$	$a^\alpha = \frac {d^2 x^\alpha}{d\tau^2}$	Sí
Volumen			Sí

Ecuación líneas geodésicas

El tensor de Riemann y la curvatura de las líneas de universo

Véanse también: Tensor de curvatura, Transporte paralelo y Fuerza de marea.

Aproximación de dos geodésicas (en verde) en una superficie esférica. Su vector de separación $\xi$ (primero rosa, luego azul) va progresivamente contrayéndose conforme nos acercamos al Polo Norte, siguiendo las pautas marcadas por el tensor de Riemann.

La medición de la curvatura de cualquier variedad (ya se trate del espacio-tiempo, de una esfera o de una silla de montar) viene determinada por el tensor de curvatura o tensor de Riemann, que es una función de los símbolos de Christoffel y sus derivadas de primer orden.

El tensor de Riemann tiene una importancia fundamental a la hora de calcular la desviación de dos líneas en origen paralelas cuando se desplazan a través de una superficie curva. Es bien sabido que en una variedad llana las líneas paralelas jamás se cortan, sin embargo esta regla no rige en el caso de las superficies curvas de geometría elíptica. Supongamos que dos viajeros salen del Ecuador en dirección norte. En ambos casos, el ángulo que la trayectoria de su barco forma con el Ecuador es inicialmente de 90°, por lo que se trata de dos líneas paralelas. Sin embargo, conforme los viajeros se van desplazando hacia el norte, su distancia recíproca se hace cada vez más pequeña hasta que se hace nula en el Polo Norte, que es donde se cortan sus trayectorias de viaje. Para calcular la tasa de aproximación entre las dos geodésicas utilizamos la siguiente ecuación:

$d^2\xi^{\alpha} = R^{\alpha}_{\beta\mu\nu}dx^{\beta} \xi^{\mu} dx^{\nu}$

donde $\ dx^{\beta}$ y $\ dx^{\mu}$ representan el recorrido desde el Ecuador de ambas líneas geodésicas y $\ \xi^{\mu}$ la distancia de separación entre ellas.

Aceleración recíproca de dos líneas de universo geodésicas. Como vemos, conforme se avanza en la coordenada temporal, el tensor de Riemann curva las geodésicas y provoca el acercamiento recíproco de las dos partículas.

En el espacio-tiempo, que también es una variedad curva, las cosas funcionan de un modo parecido: el tensor de Riemann determina la aceleración recíproca entre las líneas de universo de dos sistemas inerciales (p. ej. dos asteroides que se acercan progresivamente como consecuencia de su mutua atracción gravitatoria). Para calcular dicha aceleración, aplicamos de nuevo la conocida fórmula, modificándola ligeramente:

$\frac{d^2\xi^{\alpha}}{d\tau^2} = R^{\alpha}_{\beta\mu\nu}u^{\beta} \xi^{\mu} u^{\nu}$

donde $d\tau$ es un parámetro afín (el tiempo local) y $u^\beta$ y $u^\mu$ son los vectores de cuadrivelocidad de ambos cuerpos que, según el esquema de Minkowski, equivalen geométricamente a campos vectoriales tangentes a ambas líneas de universo.

Fuerzas de marea

Todo esto nos conecta con lo que en física newtoniana se denominan fuerzas de marea, responsables de múltiples fenómenos astronómicos y cuya base teórica reposa en el planteamiento siguiente: Supongamos que una determinada nave espacial está cayendo a un agujero negro. Es evidente que la proa de la nave experimenta una fuerza gravitatoria más intensa que la popa, por el simple hecho de que la primera está más próxima que la segunda al horizonte de sucesos. Si la diferencia de aceleraciones entre la proa y la popa es lo suficientemente intensa, la nave puede llegar a distorsionarse y quebrarse definitivamente.

El gradiente gravitatorio es también responsable del ciclo de mareas: Las zonas de la tierra más cercanas a la Luna, experimentan una mayor atracción gravitatoria que las más lejanas a ella, lo que provoca que el agua del mar se acumule en aquellas áreas de la superficie terrestre que están alineadas con la Luna.

En relatividad general, la aceleración de marea viene originada por el tensor de Riemann. Hay una correspondencia casi natural entre las ecuaciones newtonianas y las relativistas. En efecto, la ecuación newtoniana utilizada para computar las fuerzas de marea es la siguiente:

$a^i = \Phi_{,ii}\xi^i$

donde a es la aceleración de marea, $\Phi$ el potencial gravitatorio y $\xi$ la distancia entre las dos partículas. Las fuerzas de marea vienen determinadas por las derivadas de segundo orden del potencial gravitatorio.

Desde el punto de vista relativista, las fuerzas de marea vienen determinadas por el tensor de Riemann y si la región del espacio tiene una escasa densidad de cuadrimomento y una distribución uniforme de la curvatura, los componentes toman aproximadamente los valores siguientes:

R^i_{0i0} \approx \Phi_{, ii}

R^{\alpha}_{\beta\mu\nu} \approx 0

para el resto de los índices

Demostración

Las expresiones que relacionan el tensor de Riemann con los símbolos de Christoffel son las siguientes:

$R^{\alpha}_{\beta\mu\nu} = \Gamma^{\alpha}_{\beta\nu ,\mu} - \Gamma^{\alpha}_{\beta\mu ,\nu} + \Gamma^{\sigma}_{\beta\nu}\Gamma^{\alpha}_{\sigma\mu} -\Gamma^{\rho}_{\beta\mu}\Gamma^{\alpha}_{\rho\nu}$

En un marco de Lorentz, donde se hacen nulos los coeficientes de los símbolos de Christoffel pero no así sus primeras derivadas, la fórmula para el cálculo del tensor de curvatura queda simplificada:

$R^{\alpha}_{\beta\mu\nu} = \Gamma^{\alpha}_{\beta\nu ,\mu} - \Gamma^{\alpha}_{\beta\mu ,\nu}$

Si el espacio-tiempo es newtoniano o cuasinewtoniano (poca densidad de cuadrimomento, fluidos no relativistas) los únicos coeficientes no nulos de los símbolos de Christoffel son los correspondientes a $\Gamma^{i}_{00}$ . Tenemos pues:

\Gamma^{i}_{00} = \Phi_{,i}

de lo contrario

\Gamma^{\alpha}_{\beta\mu} = 0

R^{i}_{0i0} = \Gamma^{i}_{00,i} - \Gamma^{i}_{0i,0}

R^{i}_{0i0} = \Gamma^{i}_{00,i}

R^{i}_{0i0} = \Phi_{,ii}

De ahí que sea muy simple deducir la ecuación clásica partir de la relativista:

\frac{d^2\xi^{i}}{d\tau^2} = R^{i}_{0i0}u^{0} \xi^{i} u^{0} \to a^i = \Phi_{,ii}\xi^i

Como se puede deducir de los párrafos anteriores, en relatividad general las fuerzas de marea están determinadas por el tensor de Riemann y las primeras derivadas de los símbolos de Christoffel. Si estas magnitudes tienen un valor no nulo, el diferencial de los símbolos de Christoffel provoca la dispersión de las geodésicas correspondientes a partículas de un fluido determinado.

\ \partial \Gamma^\alpha_{\beta\mu} \not = 0

\ \frac{du^\alpha}{d\tau} = -\Gamma^{\alpha}_{\mu\nu}u^\mu u^\nu

Las geodésicas (trayectorias inerciales en el espacio-tiempo) vienen determinadas por los valores de los símbolos de Christoffel. Si éstos son constantes, las partículas de un fluido se mueven uniformemente, a una misma velocidad y aceleración, y no se altera su distancia entre sí. Pero si los componentes de los símbolos de Christoffel varían a lo largo de una determinada región, ello conlleva la divergencia de las líneas de universo de las partículas y la distorsión del fluido, en la medida en que cada una de sus partes constituyentes acelera distintamente.

En esta recreación artística se reproducen el planeta y los dos cinturones de asteroides que orbitan alrededor de la estrella Épsilon Eridani.

Las fuerzas de marea y el tensor de Riemann tienen una importancia fundamental en la formación y configuración de los sistemas planetarios, así como en multitud de procesos astrofísicos y cosmológicos. Sirva de ejemplo nuestro propio Sistema Solar: Hace cerca de 4500 millones de años, una nube molecular alcanzó la densidad y la compresión suficientes como para transformarse en un sistema planetario. La mayor parte del material de la nube se precipitó sobre en torno al núcleo, dando lugar al Sol. Sin embargo, ciertas cantidades de gas y de polvo continuaron rotando bajo la forma de un disco de acreción, y se aglutinaron para dar origen a planetesimales y posteriormente a planetas.

El sistema planetario de la estrella HD 69830 viene compuesto por un masivo cinturón de asteroides y por tres exoplanetas de masa neptuniana cuyos efectos gravitatorios dispersan las líneas de universo de los asteroides, impidiendo que se agreguen para formar nuevos planetas.

Sin embargo, en la zona situada entre Marte y Júpiter, los tensores de Riemann correspondientes a las masas del Sol y de Júpiter generaron unas intensas fuerzas de marea que dispersaron las líneas de universo de los planetesimales allí situados, impidiendo que se agregaran entre sí para dar lugar a un cuerpo masivo. Los planetesimales permanecieran dispersos bajo la forma de un cinturón de asteroides. Este fenómeno que acaba de describirse no es exclusivo de nuestro Sistema Solar, sino que ha sido observado en multitud de sistemas exoplanetarios descubiertos desde principios de los años noventa hasta la actualidad, como los mostrados en las ilustraciones de esta sección.

Las fuerzas de marea también poseen cierta importancia en el desarrollo de otros fenómenos astronómicos como las supernovas de tipo II, deflagraciones cósmicas que suelen tener lugar en el marco de sistemas estelares dobles. En efecto, en los sistemas binarios es frecuente que una estrella masiva orbite alrededor de una enana blanca. Si el tamaño de la primera sobrepasa el límite de Roche, el componente del tensor de Riemann $R^{i}_{0i0}$ generado por la masa de la enana blanca extrae material de las capas exteriores de su compañera y lo precipita sobre la enana blanca, en torno a la cual dicho material orbita formando un disco de acreción. El plasma queda sometido a enormes temperaturas que provocan la emisión de rayos X y la aparición de explosiones periódicas conocidas con el nombre de supernovas de tipo II.

El significado físico del tensor de Ricci

En la ilustración se reproducen los efectos del tensor de Ricci (concretamente su componente $R^{00}$ ) sobre un volumen tridimensional esférico: conforme aumenta el tiempo, dicho volumen se reduce. El autor de la imagen se ha permitido la siguiente licencia: Aunque los ejes de coordenadas representan dos dimensiones espaciales y una temporal, el volumen de la esfera está definido por tres dimensiones espaciales.

Según la teoría laplaciana-newtoniana de la gravitación universal, una masa esférica de gas reduce su volumen (como consecuencia de la atracción recíproca de sus moléculas) con una aceleración equivalente a $4G\pi \rho\;$ :

$\Delta V =4\pi G \rho\;$

Es evidente, que dicha ecuación no es compatible con la relatividad especial, por las razones reseñadas anteriormente:

El parámetro $\rho\,$ , que mide la densidad de masa, ha de ser sustituido por el tensor de energía-tensión $T^{\alpha \beta}\,$ , que permanece invariable ante las transformaciones de Lorentz y tiene en cuenta los efectos gravitatorios de la energía y la presión, y nosolo los de la masa.
Por otro lado, según la teoría de la relatividad general, los efectos gravitatorios no son causados por ningún tipo de fuerza a distancia sino por la curvatura del espacio-tiempo.

En este sentido, cabe señalar que en un espacio-tiempo curvo la aceleración del volumen viene cuantificada por un objeto geométrico específico, el tensor de Ricci $R^{\alpha \beta}\,$ , que puede definirse como la aceleración coordenada del hipervolumen $\Pi_\beta$ , normal al vector unitario $e_\beta\,$ . De este modo, el componente $R^{00}\,$ expresa la aceleración temporal del volumen tridimensional:

$\ R^{00} = \frac{d^2 \Pi_0}{d(x^0)^2} \quad \Rightarrow \quad R^{00} = \nabla^2 V$

La relación entre el tensor métrico y el tensor de Ricci se expresa a través de la llamada ecuación de flujo de Ricci, que tiene la forma siguiente:

$\partial_t g_{\alpha\beta} = -2R_{\alpha\beta}\,$

Según esta ecuación, la existencia de valores positivos del tensor de Ricci implica la disminución a lo largo del tiempo de los coeficientes del tensor métrico, y como consecuencia de ello la disminución de los volúmenes en esa región de la variedad. Por el contrario, la presencia de valores negativos en el tensor de Ricci lleva consigo una expansión progresiva de las distancias, las superficies y los volúmenes.

Por todo lo dicho, los tensores de energía-momentum y de Ricci permitían expresar de manera tensorial y covariante la fórmula de Poisson, y de ahí que originalmente Einstein propusiera las siguientes ecuaciones de universo:

$\ R^{\alpha\beta} = \frac{4\pi G}{c^2} T^{\alpha\beta}$

En relatividad general, el tensor de Ricci tiene la virtualidad de representar aquellos efectos gravitatorios originados por la presencia inmediata y local de cuadrimomento, que son con gran diferencia los más importantes a pequeña y gran escala.

El tensor de Ricci rige, pues, la mayor parte de los procesos astrofísicos que tienen lugar en el Cosmos: constituye una medida de la contracción de nubes moleculares que dan lugar al nacimiento de estrellas y planetas; cuantifica el colapso de las grandes cuerpos estelares y su conversión en enanas blancas, estrellas de neutrones y agujeros negros; y proporciona una medida de la expansión del universo.

Del tensor de Ricci, particularmente de la forma que toma en los campos gravitatorios esféricos (como las estrellas estáticas), se deriva la llamada Ley de equilibrio hidrostático, que regula el equilibrio entre la presión del fluido estelar (que tiende a expandir el volumen de la estrella) y la curvatura gravitatoria (que lo contrae). Este equilibrio se mantiene prácticamente durante toda la vida de la estrella y solo se rompe en dos ocasiones diferentes: 1) Cuando la estrella deviene en una gigante roja, en cuyo caso los efectos de la presión de radiación desbordan los del tensor de Ricci, y como resultado, el volumen de la estrella se expande hasta alcanzar una nueva situación de equilibrio. 2) Cuando la estrella agota su combustible. Se produce entonces un descenso en la presión del fluido, y la estrella, bien se transforma en una enana blanca, en una estrella de neutrones, o bien colapsa definitivamente convirtiéndose en un agujero negro.

Las ecuaciones de Universo de Einstein

Einstein tuvo pronto que modificar ligeramente sus ecuaciones de universo, pues estas no eran compatibles con la ley de la conservación de la energía [Demostración 1]. Esto constriñó a Einstein a modificar sus ecuaciones de Universo, que adquirieron su forma definitiva tras la publicación en 1915 del artículo Aplicación de la teoría de la relatividad general al campo gravitatorio:

$R^{\alpha \beta} - \frac{1}{2}g^{\alpha \beta}R = \frac{8\pi G}{c^4} T^{\alpha \beta}$

Demostración 1

En efecto, la derivada covariante del tensor de energía-momentum de cualquier fluido es cero:

\ \nabla_\beta T^{\alpha \beta} = 0

Sin embargo, de las identidades de Bianchi se deduce que la derivada covariante del tensor de Ricci es en general no nula:

R^{\alpha}_{\beta ( \mu \nu \sigma )} = 0 \to R^{\alpha}_{\beta \mu \nu , \sigma} + R^{\alpha}_{\beta \sigma \mu , \nu} + R^{\alpha}_{\beta \nu \sigma , \mu} = 0

\ \nabla_\beta (R^{\alpha \beta} - \frac{1}{2} g^{\alpha \beta}R) = 0 \to \nabla_\beta R^{\alpha \beta} \not = 0

Lo que conduce al descarte de cualquier tipo de relación de proporcionalidad entre el tensor de Ricci y el tensor de tensión energía:

R^{\alpha \beta} \not = kT^{\alpha \beta}

Donde $R^{\alpha \beta}\,$ es el tensor de Ricci, $g^{\alpha \beta}\,$ el tensor métrico, $R\,$ el escalar de Ricci, $G\,$ la constante de gravitación universal y $T^{\alpha \beta}\,$ el tensor de energía-impulso. El miembro izquierdo de la ecuación recibe el nombre genérico de tensor de Einstein, se representa con la notación $G^{\alpha \beta}\,$ y satisface las mismas relaciones de conservación que el tensor de tensión-energía:

$\nabla_{\beta}G^{\alpha \beta} = \nabla_{\beta} \left( R^{\alpha \beta} - \frac{1}{2}g^{\alpha \beta}R \right) = 0, \qquad \ G^{\alpha \beta} = kT^{\alpha \beta}$

Teniendo en cuenta que el escalar de curvatura $R$ es proporcional a la traza del tensor de Einstein $G^\alpha_\alpha\,$ , las ecuaciones de universo de Einstein pueden reformularse de la manera siguiente:

$\ -R = G^\alpha_\alpha = \frac{8\pi G}{c^4}T$

$\ R_{\alpha \beta} = \frac{8\pi G}{c^4} \left( T_{\alpha \beta} - \frac{1}{2}g_{\alpha \beta}T \right)$

Aplicación a fluido perfecto

Corriente de chorro emanando del centro de una galaxia

En un fluido no relativista, como una nebulosa o una estrella de la secuencia principal, todos los componentes del tensor de energía-impulso son nulos o de muy poca importancia, salvo el elemento $T_{00} = \rho c^2\,$ , que corresponde a la densidad de masa y que es el único que contribuye sensiblemente a la atracción gravitatoria y a la curvatura del espacio-tiempo. Si deseamos medir la contracción de volumen producida por la masa-energía presente en una determinada región, hemos de aplicar las ecuaciones de universo de Einstein:

$\ R_{\alpha\beta} = \frac{8\pi G}{c^2} \left(T_{\alpha\beta} - \frac{1}{2} g_{\alpha\beta}T \right)$

Computemos ahora los valores de $R_{00}$ :

$R_{00} = \frac{8\pi G}{c^2} \left(T_{00} - \frac{1}{2} g_{00}T \right)$

Tras ello obtenemos:

$T \approx c^2T_{00} \to R_{00} = \frac{4\pi G}{c^2} T_{00}$

O bien:

\nabla^2 V = {8\pi G} \left(\rho - \frac{\rho c^2 - 3P}{2c^2} \right) = 4\pi G \left(\rho + 3\frac{P}{c^2} \right)

Donde $P\,$ es la presión del fluido, que en general es muy pequeña comparada con $\rho c^2\,$ , por lo que tenemos es una ligera corrección de la anteriormente citada fórmula newtoniana. Como vemos, la atracción gravitatoria viene determinada no solo por la masa-energía sino también por la presión, aunque la contribución de ésta es $c^2$ inferior a la de la primera. Por eso, en las regiones del espacio-tiempo sometidas a bajas presiones y temperaturas, como las nebulosas o nuestro Sistema Solar, la masa es prácticamente la única fuente de atracción gravitatoria y por ello las ecuaciones de la gravitación universal newtonianas constituyen una muy buena aproximación de la realidad física. En cambio, en fluidos sometidos a altas presiones, como las estrellas que se colapsan, la materia que se precipita en los agujeros negros o los chorros que son expelidos de los centros de las galaxias; en todos ellos la presión puede tener cierta importancia a la hora de computar la atracción gravitatoria y la curvatura del espacio-tiempo.

Aplicación a fluido electromagnético

La deflexión relativista de los rayos de la luz genera las conocidas «lentes gravitacionales».

En un fluido electromagnético, la traza del tensor de energía-impulso es nula. Como consecuencia de ello, las ecuaciones de universo de Einstein toman la siguiente forma.

$R_{00} = \frac{8\pi G}{c^2} \left(T_{00} - \frac{1}{2} g_{00}T \right)$

$T=0 \to R_{00} = \frac{8\pi G}{c^2} \left(T_{00}\right)$

Como vemos, los valores del tensor de Ricci son justo el doble de los calculados para las soluciones de polvo. Esto es lo que explica que la deflexión de los rayos de la luz sea dos veces superior en el ámbito relativista que en el newtoniano, y que la expansión de un universo cíclico de Tolman (dominado por la radiación) sea más lenta que la de un universo cíclico de Friedman (dominado por la materia).

El tensor de Weyl

Es importante notar que, puesto en un espacio-tiempo de cuatro dimensiones, el tensor pleno de curvatura contiene más información que la curvatura de Ricci. Eso significa que las ecuaciones del campo anterior, con Λ = 0, no especifican completamente el tensor de curvatura sino una parte del mismo, el tensor de Ricci. La parte de la curvatura no especificada por las ecuaciones de Einstein, coincide precisamente con el tensor de Weyl. Eso significa que las ecuaciones de Einstein no especifican por completo el tensor de curvatura, ni la forma global del universo.

La constante cosmológica

Véase también: Constante cosmológica

Desde el principio Einstein apreció que matemáticamente el miembro derecho de su ecuación de campo podía incluir un término proporcional al tensor métrico sin que se violara el principio de conservación de la energía. Aunque inicialmente no incluyó dicho término, ya que no parecía tener una interpretación física razonable, más tarde lo incluyó. Esto se debió a que en sus primeros intentos de encontrar soluciones exactas a las ecuaciones de campo consideró que lo que hoy conocemos como modelo estacionario de Einstein. Einstein apreció que esa solución, explicaba adecuadamente los datos disponibles en su tiempo, y correspondía a un universo estático similar a los datos observados. Sin embargo, dicha solución era inestable matemáticamente lo cual no parecía corresponderse con la estabilidad física observable, y se dio cuenta de que con el término proporcional a la métrica la solución podía ser similar pero esta vez estable.

Por esa razón Einstein introdujo en sus ecuaciones un término proporcional al tensor métrico. Siendo la constante de proporcionalidad precisamente la constante cosmológica. El trabajo de varios científicos (FLRW): Alexander Friedman, Georges Lemaître, Howard Percy Robertson y Arthur Geoffrey Walker, probó que existían soluciones estables no estacionarios sin el término proporcional a la constante cosmológica. Y aunque Einstein inicialmente había rechazado el trabajo de Friedman por describir un universo en expansión que no parecía ser descriptivamente adecuado a un universo que él creía estacionario, los datos del corrimiento al rojo del astrónomo Edwin Hubblesolo parecían explicables mediante un modelo de universo en expansión. Esto convenció a Einstein de que la solución FLRW era de hecho correcta y descriptivamente adecuada y por tanto la constante cosmológica innecesaria.

Recientemente la evidencia de la aceleración de la expansión del Universo han llevado a reintroducir la constante cosmológica diferente de cero como una de las posibles explicaciones del fenómeno.

Resumen

**Significado físico de los diferentes tensores de la Relatividad general**
Tensor	Notación	Significado físico
Derivada ordinaria	$\frac{du^\alpha}{dt}$	Aceleración medida por un observador externo en reposo
Derivada covariante	$\nabla_{\vec u} \vec u$	Aceleración inercial medida por un observador comóvil, situado en la propia línea de universo del cuerpo observado
Tensor métrico	$\ g_{\alpha\beta}$	Distancia (o, en su caso, intervalo) entre dos puntos (eventos) del espacio(-tiempo)
Tensor de tensión energía	$\ T_{\mu\nu}$	Presencia inmediata de cuadrimomento en una región del espacio-tiempo
Tensor de Riemann	${R^\alpha}_{\beta\mu\nu}$	Aceleración recíproca de dos líneas de universo
Tensor de Ricci	$\ R_{\mu\nu}$	Aceleración de un volumen (3 dimensiones) o un hipervolumen (4 dimensiones)
Escalar de Ricci	$\ R$	Aceleración de la superficie que encierra dicho volumen o hipervolumen
Tensor de Weyl	$\ C^\alpha_{\beta\mu\nu}$	Fuerzas de marea generadas por las ondas gravitatorias

**Principales ecuaciones de la relatividad general**
Denominación	Desarrollo	Significado físico
Ecuaciones de universo de Einstein		Contracción de un fluido como consecuencia de la presencia inmediata de cuadrimomento
Ecuación de las líneas geodésicas		Movimiento de un sistema inercial en el espacio-tiempo
Desviación geodésica		Fuerzas de marea entre dos partículas que caen en un mismo campo gravitatorio

Soluciones de las ecuaciones de campo de Einstein

Matemáticamente las ecuaciones de campo de Einstein son complicadas porque constituyen un sistema de 10 ecuaciones diferenciales no lineales independientes. La complejidad de dicho sistema de ecuaciones y las dificultades asociadas para plantear el problema como un problema de valor inicial bien definido, hicieron que durante mucho tiempo solo se contara con un puñado de soluciones exactas caracterizadas por un alto grado de simetría. En la actualidad se conocen algunos centenares de soluciones exactas de las ecuaciones de Einstein.

Históricamente la primera solución importante fue obtenida por Karl Schwarzschild en 1915. Esta solución, conocida posteriormente como métrica de Schwarzschild, representa el campo creado por un astro estático y con simetría esférica. Dicha solución constituye una muy buena aproximación al campo gravitatorio dentro del sistema solar, lo cual permitió someter a confirmación experimental la teoría general de la relatividad, explicándose hechos previamente no explicados, como el avance del perihelio de Mercurio y prediciendo nuevos hechos más tarde observados, como la deflexión de los rayos de luz de un campo gravitatorio. Además, las peculiaridades de esta solución condujeron al descubrimiento teórico de la posibilidad de los agujeros negros, y se abrió todo una nueva área de la cosmología relacionada con ellos. El estudio del colapso gravitatorio y los agujeros negros condujo a la predicción de las singularidades espaciotemporales, deficiencia que revela que la teoría de la relatividad general es incompleta.

Algunas otras soluciones físicamente interesantes de las ecuaciones de Einstein son:

La métrica de Kerr que describe el campo gravitatorio de un astro en rotación. Esta solución bajo ciertas circunstancias también contiene un agujero negro de Kerr.
La métrica de Friedman-Lemaître-Robertson-Walker, realmente es un conjunto paramétrico de soluciones asociadas a la teoría del Big Bang que es capaz de explicar la estructura del universo a gran escala y la expansión del mismo.
El universo de Gödel, que en su forma original no parece describrir un universo realista o parecido al nuestro, pero cuyas propiedades matemáticamente interesantes constituyeron un estímulo para buscar soluciones más generales de las ecuaciones, para ver si ciertos fenómenos eran o no peculiares de las soluciones más sencillas.

Por otra parte, el espacio-tiempo empleado en la teoría especial de la relatividad, llamado espacio de Minkowski es en sí mismo una solución de las ecuaciones de Einstein, que representa un espacio-tiempo vacío totalmente de materia.

Fuera de las soluciones exactas y a efectos comparativos con la teoría de campo gravitatorio, también es interesante la aproximación para campos gravitatorios débiles y las soluciones en forma de ondas gravitatorias.

No linealidad

Cuando Einstein formuló en 1915 las ecuaciones de universo de la Relatividad general, el científico alemán pensó, en un principio, que dichas ecuaciones eran irresolubles debido a su carácter no lineal, que se manifestaba tanto desde un punto de vista físico como desde otro matemático:

En el plano estrictamente físico, la no linealidad de las ecuaciones de campo de Einstein se deriva del mutuo condicionamiento entre el tetramomentum y la curvatura del espacio tiempo. Así, la densidad de masa, contenida en el coeficiente $\ T^{00}$ , provoca una contracción (parametrizada a través de $\ R^{00}$ ) del volumen tridimensional, que de nuevo vuelve a alterar la densidad de masa, y así sucesivamente. Este movimiento cíclico recuerda a la autoinductancia del electromagnetismo y no suele tener importancia en campos gravitatorios de baja intensidad, pero sí ha de tenerse en cuenta en el cálculo de las perturbaciones gravitatorias originadas por una alta concentración local de tetramomentum, como sucede en el caso de los agujeros negros o los fluidos relativistas. De una manera más intuitiva, la no linealidad de las ecuaciones de Einstein puede pensarse desde el punto de vista físico de la siguiente manera: Dada una distribución de materia, esta producirá una curvatura del espacio o "campo gravitatorio", el cual contiene energía. Dado que E=mc², dicha energía a su vez generará otra curvatura o "campo gravitatorio", el cual a su vez contendrá cierta energía y así sucesivamente. Esta retroalimentación entre la fuente (materia) y el efecto (curvatura) está representada en el carácter no lineal de las ecuaciones de Einstein.
Desde un punto de vista matemático, el miembro izquierdo de la igualdad $R_{\alpha\beta} - \frac{1}{2}Rg_{\alpha\beta} = kT_{\alpha\beta}$ contiene tanto funciones lineales como derivadas de primer y de segundo orden del tensor métrico $\ g_{\alpha\beta}$ , lo que hace imposible despejar los coeficientes de este último a partir de los valores del tensor de energía momentum $\ T_{\alpha\beta}$ . No es posible, pues, construir una función de tipo $f:T_{\alpha\beta} \to g_{\alpha\beta}$ .

Soluciones para coordenadas esféricas: Campo exterior

Artículo principal: Métrica de Schwarzschild

Para sorpresa de Albert Einstein, pocas semanas después de la publicación de sus ecuaciones de campo llegó a su despacho un correo de Karl Schwarzschild, un profesor universitario que en esos momentos se encontraba en el frente de la I guerra mundial, realizando trabajos de balística para las unidades de artillería del ejército alemán. En esa histórica carta se contenían las primeras soluciones exactas de las ecuaciones de la relatividad general, que serían conocidas por la posteridad con el nombre genérico de Solución de Schwarzschild.

El principio sobre el que pivotaba dicha solución era el siguiente: Dado que el Principio de la Covariancia General permitía hacer funcionar las ecuaciones de campo de la relatividad general en cualquier sistema de coordenadas, Schwarzschild procedió a calcular los valores de los tensores de energía-momento y de Einstein en coordenadas espacio-temporales esféricas $\ (\theta,\phi,r,t)$ . El alto grado de simetría proporcionado por dicho sistema de coordenadas, así como el carácter estático de la métrica, permitieron integrar directamente el conjunto de ecuaciones diferenciales. Siendo en el caso general el tensor métrico para un problema con simetría esférica de la forma:

(SE) $ds^2 = -f(r)dt^2 + h(r)dr^2 + r^2(d\theta^2+\sin^2d\phi^2)\,$

Para el espacio la parte exterior de un astro esférica más concretamente se tenía:

$f(r) = \frac{1}{h(r)} = \left(1 - \frac{2GM}{c^2 r} \right)$

Las comprobaciones experimentales mostraron que la métrica de Schwarzschild describe con enorme precisión lo que sucede en sistemas esféricos estáticos, similares al sistema solar.

Soluciones para coordenadas esféricas: Equilibrio estelar

Artículo principal: Estructura estelar

La masa del Sol, así como su volumen y su temperatura se han mantenido estables durante millones de años.

Las ecuaciones de un campo con simetría esférica (SE) permiten también estudiar la curvatura en el interior de las estrellas masivas. El resultado de ese análisis, es que para estrellas de la secuencia principal del diagrama de Hertzsprung-Russell, la curvatura originada por la gravedad es compensada por la presión de la materia estelar. Esa compensación conduce a una ley de equilibrio hidrostático que hace que la estrella, aún sometida a su propio campo gravitatorio, pueda mantener durante millones de años su volumen y su densidad a niveles constantes. Matemáticamente, el hecho de que la métrica tenga un carácter estático implica los valores del tensor $\ T_{\alpha\beta}$ se mantengan estables en el tiempo. La ley de equilibrio hidrostático que relaciona la densidad y la presión en una estrella esférica viene dada por la ecuación de Tolman-Oppenheimer-Volkoff:

$\frac{dP}{dr} = -G \left(\frac{P+\rho c^2}{r}\right) \left(\frac{mc^2+4\pi r^3P}{c^2r-2Gm}\right)$

Donde:

P(r), \rho(r)\,

son la presión y la densidad a una distancia r del centro del astro.

m(r) = \int_0^r \rho(\bar{r})\ 4\pi\bar{r}^2d\bar{r}

es la masa encerrada en una esfera de radio r.

Soluciones para coordenadas esféricas: Colapso gravitatorio

La solución de Schwarzschild permitió aplicar los postulados de la relatividad general a disciplinas como la mecánica celeste y la astrofísica, lo cual supuso una verdadera revolución en el estudio de la cosmología: Apenas seis años después de la publicación de los trabajos de Einstein, el físico ruso Aleksander Fridman introdujo el concepto de singularidad espacio-temporal, definido como un punto del espacio-tiempo en el que confluyen todas las geodésicas de las partículas que habían atravesado el horizonte de sucesos de un agujero negro. En condiciones normales, la curvatura producida por la masa de los cuerpos y las partículas es compensada por la temperatura o la presión del fluido y por fuerzas de tipo electromagnético, cuyo estudio es objeto de la física de fluidos y del estado sólido. Sin embargo, cuando la materia alcanza cierta densidad, la presión de las moléculas no es capaz de compensar la intensa atracción gravitatoria. La curvatura del espacio-tiempo y la contracción del fluido aumentan cada vez a mayor velocidad: el final lógico de este proceso es el surgimiento de una singularidad, un punto del espacio-tiempo donde la curvatura y la densidad de tetramomentum son infinitas.

Ahora bien, el físico Subrahmanyan Chandrasekhar fue el primero en darse cuenta de que la gravedad podía ser contenida no solo por fuerzas de tipo mecánico, sino también por un fenómeno de origen cuántico al que llamó presión de degeneración, derivado del principio de exclusión de Pauli y que era capaz de sostener a estrellas cuya masa no superase el límite de Chandrasekhar. Estas ideas tan audaces le costaron caras a su autor, que fue ridiculizado en público por Sir Arthur Eddington durante un congreso de astrónomos. Sin embargo, los cálculos de Chandrasekhar se revelaron certeros, y sirvieron de base para la comprensión de un tipo estelar cuya naturaleza física hasta entonces era desconocida: la enana blanca.

Aproximaciones en coordenadas armónicas

Dado que para muchos sistemas físicos no resulta sencillo obtener las expresiones exactas de las soluciones de las ecuaciones de Einstein, los físicos teóricos han desarrollado aproximaciones bastante precisas empleando series de potencias. De entre ellas las más importantes funcionan en coordenadas armónicas y reciben los nombres de aproximación posnewtoniana y aproximación para campos gravitatorios débiles.

En virtud del principio de la covariancia general, ya examinado en secciones anteriores, es posible hacer funcionar a las ecuaciones de universo de Einstein en cualquier tipo de coordenadas, incluidas las armónicas, que son aquellas en las que se cumple la relación $\Gamma^{\lambda} = g_{\alpha\beta}\Gamma^{\lambda}_{\alpha\beta} = 0$ (como, por ejemplo, en el caso de las coordenadas cartesianas). Se hace necesario en este punto distinguir con claridad entre los conceptos de planitud del espacio-tiempo y armonicidad de un sistema de coordenadas: en una espacio-tiempo de curvatura nula, como el espacio-tiempo de Minkowski, es posible utilizar coordenadas no-armónicas como las esféricas o las cilíndricas, sin que ello implique que el espacio se curve, ya que la curvatura es una cualidad instrínseca de cualquier variedad e independiente de nuestro sistema de referencia.

Ondas gravitatorias. La solución en el vacío de la aproximación para campos gravitatorios débiles (

\nabla^2 h_{\alpha\beta} = \frac{1}{c^2} \frac{\partial^2 h_{\alpha\beta}}{\partial t^2}

) tiene una estructura similar a la ecuación diferencial de ondas de d'Alembert, de lo que se deduce que las perturbaciones de la métrica tienen una naturaleza ondulatoria y se transmiten a través del espacio-tiempo a la velocidad de la luz.

Para campos gravitatorios poco intensos, como los existentes en el espacio interestelar, es recomendable utilizar la llamada aproximación para campos débiles, que es, como veremos, muy similar en su estructura a la fórmula de Poisson newtoniana, si bien las diferencias con esta última son enormes.

La fórmula de Poisson afirma que el laplaciano del potencial gravitatorio $\Phi$ es igual $4G\pi$ :

$\nabla^2 \Phi = 4\pi G\rho \to \Phi (x,t) = \int_V \frac{G\rho (x',t)}{r}dV$

En la imagen se reproducen las ondas gravitatorias emitidas por una estrella durante su colapso.

Esta fórmula plantea un grave inconveniente, y es que presupone el principio de acción a distancia: No tiene en cuenta el retardo en la medición del campo gravitatorio realizada por un determinado observador (pongamos, un observador en la tierra) situado a cierta distancia a la masa del cuerpo que genera dicho campo gravitatorio (p. ej. el Sol, situado a 8 minutos luz de nuestro planeta).

De ahí que uno de los primeros intentos de compatibilizar la teoría de la Relatividad Especial y la Gravitación Universal consistiera en sustituir el laplaciano de la fórmula de Poisson por un d'Alembertiano, una de cuyas soluciones es, precisamente, un potencial retardado:

\Box^2 \Phi = 4\pi G\rho \to \Phi (x,t) = \int_V \frac{G\rho (x',t-\frac{r}{c})}{r}dV

Como vemos, el potencial gravitatorio medido por el observador en el tiempo t, es proporcional a la densidad de masa que tiene el cuerpo estelar observado en el tiempo t - r/c, donde c es la velocidad de la luz, r es la distancia entre el observador y el objeto y r/c es el retardo, es decir, el tiempo que la luz tarda en desplazarse desde la estrella en cuestión hasta el observador.

Ahora bien, la relatividad general es una teoría métrica de la gravedad, y explica los fenómenos gravitatorios en términos de perturbaciones de la métrica. Es conveniente, por tanto, introducir en nuestra ecuación el pseudotensor $\ h_{\alpha\beta}$ , que representa la desviación de los coeficientes del tensor métrico respecto a la métrica de Minkowski $\ \eta_{\alpha\beta}$ . Aplicando el límite newtoniano, en cuya virtud $\ g_{\alpha\beta}$ es igual a $\ 1 + 2\Phi$ , obtenemos el resultado siguiente:

\ g_{\alpha\beta} = \eta_{\alpha\beta} + h_{\alpha\beta}

h_{\alpha\beta} = 2\Phi \to \Box^2 h_{\alpha\beta} = 8\pi G\rho

\ \Box^2 h_{\alpha\beta} = 16\pi G (T_{\alpha \beta} - \frac{1}{2}g_{\alpha \beta}T)

Fórmula de Poisson	$\ \nabla^2 \Phi = 4\pi G\rho$
Aproximación para campos débiles	$\ \Box^2 h_{\alpha\beta} = 16\pi G (T_{\alpha \beta} - \frac{1}{2}g_{\alpha \beta}T)$

A grandes rasgos, la sustitución del laplaciano $\nabla^2$ por el d'alembertiano $\Box^2$ viene exigida por la obligada eliminación del principio de acción a distancia; el empleo del pseudotensor $\ h_{\alpha\beta}$ en lugar del potencial $\ \Phi$ como elemento definitorio del campo gravitatorio es una consecuencia de la del carácter métrico de la teoría de la relatividad general; y finalmente, la eliminación, en el lado derecho de la ecuación, del parámetro $\ \rho$ y su sustitución por la expresión tensorial $T_{\alpha \beta} - \frac{1}{2}g_{\alpha \beta}T$ viene exigida por el principio de la covariancia general.

La aproximación posnewtoniana permite a los astrónomos calcular con suma precisión la posición y el movimiento de los planetas del Sistema Solar, teniendo en cuenta los efectos relativistas.

Sin embargo, en el análisis de la evolución de sistemas astronómicos como el solar o el formado por estrellas dobles o tripoles, la aproximación para campos débiles no es útil, ya que el uso de esta última se restringe a zonas del espacio-tiempo con poca densidad de tetramomentum. En estos casos es preferida la aproximación posnewtoniana que como su propio nombre indica prescinde del empleo de la compleja notación del cálculo tensorial y describe el movimiento de los cuerpos celestes utilizando los conceptos matemáticos que empleó el propio Newton a la hora describir las leyes de la mecánica y de la gravitación universal (vectores, gradientes, etc.).

En los siglos XVIII y XIX, astrónomos como Laplace y Le Verrier habían aplicado los postulados de la mecánica newtoniana al estudio de la evolución del Sistema Solar, obteniendo unos resultados muy fructuosos: La precisión de los cálculos astronómicos obtenidos había permitido incluso prever la existencia de un planeta hasta entonces nunca observado por los astrónomos, Neptuno. Por este motivo no es de extrañar que cuando la relatividad general obtuvo pleno reconocimiento, se desarrollase por parte de los astrofísicos una aproximación que siguiera en su estructura el modelo newtoniano y que fuese fácilmente aplicable tanto por los astrónomos como por los ordenadores.

De acuerdo con la teoría clásica de la gravitación, la aceleración de un cuerpo en caída libre es el gradiente negativo del potencial gravitatorio:

a = -\nabla\phi

Como ya se ha avanzado en secciones anteriores, esta fórmula presupone la asunción del principio newtoniano de acción a distancia, contrario a los postulados de la Relatividad Especial, y además no tiene en cuenta los efectos gravitatorios generados por la energía y por el momentum. La aproximación posnewtoniana soslaya estos inconvenientes introduciendo otros dos nuevos potenciales: el potencial $\ \psi$ , que constituye una aproximación en segundo grado del potencial $\ \phi$ y el potencial $\ \zeta$ , derivado de la presencia de momentum en el fluido.

**Potenciales de la aproximación posnewtoniana**
Notación	Expresión Algebraica	Significado físico
$\ \phi$	$\ \phi = -\int\frac{G\rho}{r}dV$	Potencial newtoniano (densidad de masa)
$\ \psi$	$\ \psi = [\frac{1}{4\pi}\frac{\partial^2 \phi}{\partial t^2} + G(E_k + E_p) + G(E_k)]$	Retardo del potencial newtoniano, densidad de energía
$\ \zeta$	$\ \zeta = -4G\int\frac{P}{r}dV$	Potencial derivado del momentum

Las ecuaciones de movimiento quedarían reformuladas de la siguiente forma:

a = -\nabla(\phi +\frac{2\phi^2}{c^2} +\psi) - \frac{1}{c}\frac{\partial\zeta}{\partial t} + \frac{v}{c} \times (\nabla \times \zeta) + \frac{3}{c^2}v\frac{\partial \phi}{\partial t} + \frac{4}{c^2}v(v\cdot\nabla)\phi -\frac{v^2}{c^2}\nabla\phi

a = -\nabla\phi + \eta

\eta = -\nabla(\frac{2\phi^2}{c^2} +\psi) - \frac{1}{c}\frac{\partial\zeta}{\partial t} + \frac{v}{c} \times (\nabla \times \zeta) + \frac{3}{c^2}v\frac{\partial \phi}{\partial t} + \frac{4}{c^2}v(v\cdot\nabla)\phi -\frac{v^2}{c^2}\nabla\phi

Solución de la fuerza total relativista

En la relatividad general, la energía potencial gravitatoria efectiva de un objeto de masa m que se mueve alrededor de un cuerpo masivo central M viene dada por

$U_f(r) =-\frac{GMm}{r}+\frac{L^{2}}{2mr^{2}}-\frac{GML^{2}}{mc^{2}r^{3}}$

Entonces se puede obtener una fuerza total conservativa como

$F_f(r)=-\frac{GMm}{r^{2}}+\frac{L^{2}}{mr^{3}}-\frac{3GML^{2}}{mc^{2}r^{4}}$

donde L es el momento angular. El primer término representa la fuerza de gravitación newtoniana, que se describe mediante la ley del cuadrado inverso. El segundo término representa la fuerza centrífuga en el movimiento circular. El tercer término está relacionado con la fuerza de Coriolis en el sistema de referencia en rotación, que incluye el inverso de la distancia a la cuarta potencia.

Soluciones relacionadas con los modelos de Universo

Existen un cierto número de soluciones exactas de las ecuaciones que describen un universo completo y por tanto pueden ser consideradas modelos cosmológicos entre ellas destacan:

Métrica de Friedman-Lemaître-Robertson-Walker, que describe un tipo de universo homogéneo, isótropo y en expansión y puede considerarse una primera aproximación de la forma de nuestro universo a gran escala.
Universo de Gödel, obtenida por el matemático Kurt Gödel representa un universo homogéneo e isótropo con materia en rotación. Aunque no se considera que describa un universo similar al nuestro tiene la importante propiedad de contener curvas temporales cerradas que representan un ejemplo contraintuitivo donde un observador puede viajar a su propio pasado sin violar ninguna ley física conocida.

Predicciones de la relatividad general

La más famosa de las primeras verificaciones positivas de la teoría de la relatividad, ocurrió durante un eclipse solar de 1919, que se muestra en la imagen tomada por Sir Arthur Eddington de ese eclipse, que fue usada para confirmar que el campo gravitatorio del sol curvaba los rayos de luz de estrellas situadas tras él.

Se considera que la teoría de la relatividad general fue comprobada por primera vez en la observación de un eclipse total de Sol en 1919, realizada por Sir Arthur Eddington, en la que se ponía de manifiesto que la luz proveniente de estrellas lejanas se curvaba al pasar cerca del campo gravitatorio solar, alterando la posición aparente de las estrellas cercanas al disco del Sol. Desde entonces muchos otros experimentos y aplicaciones han demostrado las predicciones de la relatividad general. Entre algunas de las predicciones se encuentran:

Efectos gravitacionales

Desviación gravitacional de luz hacia el rojo en presencia de campos con intensa gravedad: La frecuencia de la luz decrece al pasar por una región de elevada gravedad. Confirmado por el experimento de Pound y Rebka (1959).
Dilatación gravitacional del tiempo: Los relojes situados en condiciones de gravedad elevada marcan el tiempo más lentamente que relojes situados en un entorno sin gravedad. Demostrado experimentalmente con relojes atómicos situados sobre la superficie terrestre y los relojes en órbita del Sistema de Posicionamiento Global (GPS por sus siglas en inglés). También, aunque se trata de intervalos de tiempo muy pequeños, las diferentes pruebas realizadas con sondas planetarias han dado valores muy cercanos a los predichos por la relatividad general.
Efecto Shapiro (dilatación gravitacional de desfases temporales): Diferentes señales atravesando un campo gravitacional intenso necesitan mayor tiempo para atravesar dicho campo.
Decaimiento orbital debido a la emisión de radiación gravitacional. Observado en púlsares binarios.
Precesión geodésica: Debido a la curvatura del espacio-tiempo, la orientación de un giroscopio en rotación cambiará con el tiempo. Esto se comprobó exitosamente en mayo de 2011 por el satélite Gravity Probe B.

Efectos rotatorios

Esto implica el comportamiento del espacio-tiempo alrededor de un objeto masivo rotante.

Fricción del marco de referencia. Un objeto en plena rotación va a arrastrar consigo al espacio-tiempo, causando que la orientación de un giroscopio cambie con el tiempo. Para una nave espacial en órbita polar, la dirección de este efecto es perpendicular a la precisión geodésica.
El principio de equivalencia fuerte: incluso objetos que gravitan en torno a ellos mismos van a responder a un campo gravitatorio externo en la misma manera que una partícula de prueba lo haría.

Solución a las curvas de rotación galácticas

Una solución alternativa basada en la relatividad general propuesta por Adrián Cornejo, que considera los patrones de velocidad del gas en galaxias simuladas, según la teoría de onda de densidad cuasi-estacionaria que caracteriza a las espirales como patrones de rotación rígida y de larga duración (es decir, espirales estables), y la hipótesis de que las galaxias espirales rotarían establemente en su mayoría como un cuerpo sólido rígido, de acuerdo con la cinemática del sólido rígido, calculó la velocidad de algunas galaxias espirales tipo Sa (de acuerdo a la clasificación morfológica de las galaxias), graficando las curvas de rotación y obteniendo (sin considerar materia oscura) curvas muy aproximadas a las curvas de rotación conocidas a partir de las observaciones. La ecuación resulta de igualar la fuerza centrífuga con la fuerza que se adiciona a la mecánica newtoniana en la solución relativista (que es la fuerza inversamente proporcional a la cuarta potencia de la distancia r, relacionada con la fuerza de Coriolis en el sistema de referencia no inercial), de forma análoga a como se deriva la velocidad orbital de los planetas mediante la mecánica newtoniana. De esta forma, se tiene la fuerza de Coriolis en el sistema rotante, la cual es una fuerza que en la mecánica newtoniana no se considera en un sistema de referencia en rotación. Con lo que se tiene en el sistema rotante la fuerza que, de otra forma, se busca agregar mediante la materia oscura para ajustarse a las velocidades de rotación observadas. La ecuación en función del momento angular se da como

$v=\left(\frac{{3GM_{\bullet}J^{2}}}{{c^{2}r^{3}M_{g}^{2}}}\right)^{1/2}=\left(\frac{{3GM_{\bullet}j^{2}}}{{c^{2}r^{3}}}\right)^{1/2}$

donde c es la velocidad de la luz, J es el momento angular del sistema, j es el momento angular relativo específico, M_● es la masa del núcleo galáctico y M_g es la masa de la galaxia. Esta fórmula solamente aplica para las galaxias espirales tipo Sa debido a su simetría circular, ya que para los otros tipos de galaxias espirales con diferente morfología se tendría que considerar su distinta geometría y dinámica. Aun cuando hasta la fecha no hay muchas observaciones documentadas del momento angular de las galaxias espirales, y las estimaciones que se tienen son principalmente derivadas de modelos que utilizan el concepto de materia oscura, el momento angular de cada galaxia se puede estimar a partir del momento angular relativo específico, dado como h = L/m, o en este caso como j = J/M_g. El momento angular adecuado para cada caso se podrá verificar con observaciones más detalladas de las galaxias espirales.

Otros efectos

Gravitones: De acuerdo con la teoría cuántica de campos, la radiación gravitacional debe ser compuesta por cuantos llamados gravitones. La relatividad general predice que estos serán partículas de espín 2. Todavía no han sido observados.

Comprobaciones

La teoría de la relatividad general ha sido confirmada en numerosas formas desde su aparición. Por ejemplo, la teoría predice que la línea del universo de un rayo de luz se curva en las proximidades de un objeto masivo como el Sol. La primera comprobación empírica de la teoría de la relatividad fue a este respecto. Durante los eclipses de 1919 y 1922 se organizaron expediciones científicas para realizar esas observaciones, entre ellas la expedición de Arthur Eddington. Después se compararon las posiciones aparentes de las estrellas con sus posiciones aparentes algunos meses más tarde, cuando aparecían de noche, lejos del Sol. Einstein predijo un desplazamiento aparente de la posición de 1,745 segundos de arco para una estrella situada justo en el borde del Sol, y desplazamientos cada vez menores de las estrellas más distantes. Se demostró que sus cálculos sobre la curvatura de la luz en presencia de un campo gravitatorio eran exactos. En los últimos años se han llevado a cabo mediciones semejantes de la desviación de ondas de radio procedentes de cuásares distantes, utilizando interferómetros de radio. Las medidas arrojaron unos resultados que coincidían con una precisión del 1% con los valores predichos por la relatividad general.

Otra confirmación de la relatividad general está relacionada con el perihelio del planeta Mercurio. Hacía años que se sabía que el perihelio (el punto en que Mercurio se encuentra más próximo al Sol) gira en torno al Sol una vez cada tres millones de años, y ese movimiento no podía explicarse totalmente con las teorías clásicas. En cambio, la teoría de la relatividad sí predice todos los aspectos del movimiento, y las medidas con radar efectuadas recientemente han confirmado la coincidencia de los datos reales con la teoría con una precisión de un 0,5%.

Se han realizado otras muchas comprobaciones de la teoría, y hasta ahora todas parecen confirmarla. Prácticamente con la más reciente prueba del satélite Gravity Probe B, se podría considerar a la teoría como una ley.

Aplicaciones prácticas

Los relojes en los satélites GPS requieren una sincronización con los situados en tierra para lo que hay que tener en cuenta la teoría general de la relatividad y la teoría especial de la relatividad. Si no se tuviese en cuenta el efecto que sobre el tiempo tiene la velocidad del satélite y su gravedad respecto a un observador en tierra, se produciría un adelanto de 38 microsegundos por día en el reloj del satélite (sin corrección, su reloj retrasaría al día 7 microsegundos como consecuencia de la velocidad y adelantaría 45 microsegundos por efecto de la gravedad), que a su vez provocarían errores de varios kilómetros en la determinación de la posición. Puede considerarse otra comprobación de ambas teorías.

Relación con otras teorías físicas

En esta parte, la mecánica clásica y la relatividad especial están entrelazadas debido a que la relatividad general en muchos modos es intermediaria entre la relatividad especial y la mecánica cuántica.

Sujeto al principio de acoplamiento mínimo, las ecuaciones físicas de la relatividad especial pueden ser convertidas a su equivalente de la relatividad general al reemplazar la métrica de Minkowski (η_ab) con la relevante métrica del espacio-tiempo (g_ab) y reemplazando cualquier derivada normal con derivadas covariantes.

Inercia

Tanto en mecánica cuántica como en relatividad se asumía que el espacio, y más tarde el espacio-tiempo, eran planos. En el lenguaje de cálculo tensorial, esto significaba que R^a_bcd = 0, donde R^a_bcd es el tensor de curvatura de Riemann. Adicionalmente, se asumía que el sistema de coordenadas era un sistema de coordenadas cartesianas. Estas restricciones le permitían al movimiento inercial ser descrito matemáticamente como:

$\ddot{x}^a = 0,$ donde

x^a es un vector de posición,
$\dot{} = \partial / \partial\tau$ , y
τ es tiempo propio.

Hay que notar que en la mecánica clásica, x^a es tridimensional y τ ≡ t, donde t es una coordenada de tiempo.

En la relatividad general, si estas restricciones son usadas en la forma de espacio-tiempo y en el sistema de coordenadas, éstas se perderán. Ésta fue la principal razón por la cual se necesitó una definición diferente de movimiento inercial. En relatividad especial, el movimiento inercial ocurre en el espacio de Minkowski como parametrizada por el tiempo propio. Esto se generaliza a espacios curvos matemáticamente mediante la ecuación de las geodésicas:

$\ddot{x}^a + {\Gamma^a}_{bc} \, \dot{x}^b \,\dot{x}^c = 0,$ donde

${\Gamma^a}_{bc}$ es un símbolo de Christoffel (de otro modo conocido como conexión de Levi-Civita).

Como x es un tensor de rango uno, estas ecuaciones son cuatro y cada una está describiendo la segunda derivada de una coordenada con respecto al tiempo propio. (En la métrica de Minkowski de la relatividad especial, los valores de conexión son todos ceros. Esto es lo que convierte a las ecuaciones geodésicas de la relatividad general en $\ddot{x}^a = 0$ para el espacio plano de la relatividad especial).

Gravitación

En gravitación, la relación entre la teoría de la gravedad de Newton y la relatividad general son gobernadas por el principio de correspondencia: la relatividad general tiene que producir los mismos resultados, así como la gravedad lo hace en los casos donde la física newtoniana ha demostrado ser certera.

Alrededor de objetos simétricamente esféricos, la teoría de la gravedad de Newton predice que los otros objetos serán acelerados hacia el centro por la ley:

$\mathbf{F} = -\frac{GM.m}{r^2}\mathbf{\hat{r}}$

Donde: M: masa que genera el Campo gravitatorio, y m es la masa del cuerpo que es atraído.

r\,

, es la distancia al objeto atraído, y

\mathbf{\hat{r}}

es un vector de unidad identificando la dirección al objeto masivo.

En la aproximación de campo débil de la relatividad general tiene que existir una aceleración en coordenadas idénticas. En la solución de Schwarzschild, la misma aceleración de la fuerza de gravedad es obtenida cuando la constante de integración es igual a 2m (donde m = GM/c²).

Electromagnetismo

El electromagnetismo planteó un obstáculo fundamental para la mecánica clásica, debido a que las ecuaciones de Maxwell no son invariantes según la relatividad galileana. Esto creaba un dilema que fue resuelto por el advenimiento de la relatividad especial. En forma tensorial, las ecuaciones de Maxwell son:

$\partial_a\,F^{\,ab} = (4\pi/c)\,J^{\,b}$ , y
$\partial^{a}\,F^{\,bc} + \partial^{b} \, F^{\,ca} + \partial^{c} \, F^{\,ab} = 0$

Donde:

F_{ab}\,

, es el tensor de campo electromagnético, y

J_a\,

, es una cuadricorriente.

El efecto de un campo electromagnético en un objeto cargado de masa m es entonces:

$\frac{dP^a}{d\tau} = \frac{q}{m}P_bF^{ab}$

Donde

P^a\,

es el cuadrimomento del objeto cargado.

En la relatividad general, las ecuaciones de Maxwell se convierten en

$\nabla_a\,F^{\,ab} = (4\pi/c)\,J^{\,b}$ , y
$\nabla^a\,F^{\,bc} + \nabla^b \, F^{\,ca} + \nabla^c \, F^{\,ab} = 0$ .

La ecuación para el efecto del campo electromagnético sigue siendo la misma, aunque el cambio de métrica modificará sus resultados. Nótese que al integrar esta ecuación para cargas aceleradas las hipótesis habituales no son válidas (ya que implican que una carga sujeta en un campo gravitato debe comportarse como si estuviera uniformemente acelerada, lo que muestra que una carga uniformemente acelerada no puede radiar).

Conservación de energía-momentum

En la mecánica clásica, la conservación de la energía y el momentum son manejados separadamente. En la relatividad especial, la energía y el momentum están unidos en el cuadrimomento y los tensores de energía. Para cualquier interacción física, el tensor de energía-impulso ${T_a}^b$ satisface la ley local de conservación siguiente:

$\partial_b \, {T_a}^b = 0$

En la relatividad general, esta relación es modificada para justificar la curvatura, convirtiéndose en:

$\nabla_b \, {T_a}^b = \partial_b \, {T_a}^b + {\Gamma^b}_{cb} \, {T_a}^c + {\Gamma^c}_{ab} \, {T_c}^b = 0$

donde ∇ representa aquí la derivada covariante.

A diferencia de la mecánica clásica y la relatividad especial, en la relatividad general no es siempre posible definir claramente la energía total y el momentum. Esto a menudo causa confusión en espacio-tiempos dependientes del tiempo, en los que no existen vectores de Killing temporales, los cuales no parecen conservar energía, aunque la ley local siempre se satisfaga (Ver energía de Arnowitt, Deser y Misner).

Transición de la relatividad especial a la relatividad general

Artículo principal: Transición de la relatividad especial a la relatividad general

La teoría de la relatividad especial presenta covariancia de Lorentz; esto significa que, tal como fue formulada, las leyes de la física se escriben del mismo modo para dos observadores que sean inerciales. Einstein estimó, inspirado por el principio de equivalencia que era necesaria una teoría que presentara una para la que valiera un principio de covariancia generalizado, es decir, en que las leyes de la física se escribieran de la misma forma para todos los posibles observadores, fueron estos inerciales o no; eso le llevó a buscar una teoría general de la relatividad. Además el hecho de que la propia teoría de la relatividad fuera incompatible con el principio de acción a distancia le hizo comprender que necesitaba además que esta teoría general incorporase una descripción adecuada del campo gravitatorio.

Hoy sabemos que Einstein consideraba que la teoría de la relatividad solo era aplicable a sistemas de referencia inerciales estrictamente, aunque Logunov ha probado en el marco de la teoría relativista de la gravitación que de hecho fijado un observador inercial o no, cualquier otro que se mueva con velocidad uniforme respecto al primero escribirá las leyes físicas de la misma forma. Probando así que la relatividad especial de hecho es más general de lo que Einstein creyó en su momento. Además el trabajo de Logunov prueba que siempre que el espacio-tiempo sea plano puede establecerse para cada observador existe un grupo decaparamétrico de transformaciones de coordenadas que generaliza las propiedades del grupo de Lorentz para observadores no inerciales.

El principio de geometrización y el principio de equivalencia fueron las piedras angulares en las que Einstein basó su búsqueda de una nueva teoría, tras haber fracasado en el intento de formular una teoría relativista de la gravitación a partir de un potencial gravitatorio. La teoría escalar de la gravitación de Nordström y la interpretación geométrica que extrajo de ella Adriaan Fokker (1914), el estudiante de doctorado de Hendrik Lorentz, llevaron a Einstein a poder relacionar el tensor de energía-impulso con la curvatura escalar de Ricci de un espacio-tiempo con métrica:

$g_{\alpha \beta} = \phi\eta_{\alpha\beta}\,$

que involucraba la métrica del espacio-tiempo plano y un campo escalar relacionado con el campo gravitatorio. La superación de las deficiencias de la teoría de la gravitación escalar de Nordström llevaron a Einstein a formular las ecuaciones correctas de campo.

Véase también

En inglés: General relativity Facts for Kids

Teoría relativista de la gravitación
Teoría de la Relatividad Especial
Introducción matemática a la relatividad general
Glosario de conceptos relativistas

Obtenido de «https://ninos.kiddle.co/index.php?title=Relatividad_general&oldid=3837571»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Relatividad general para Niños. Enciclopedia Kiddle.