Sistema de numeración para niños
Un sistema de numeración es una forma de usar un grupo de símbolos y reglas para escribir y entender los números. A lo largo de la historia, las personas han usado muchos sistemas diferentes para contar y registrar cantidades.
Contenido
¿Qué es un sistema de numeración?
Un sistema de numeración es como un lenguaje especial para los números. Tiene:
- Un conjunto de símbolos que puedes usar. Por ejemplo, en nuestro sistema decimal, los símbolos son 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9.
- Unas reglas que te dicen cómo combinar esos símbolos para formar números válidos y cómo realizar operaciones con ellos.
Cada sistema tiene sus propias reglas. Por ejemplo, el sistema que usamos hoy (el decimal) tiene reglas muy sencillas para sumar o restar, mientras que el sistema de los números romanos tiene reglas un poco más complejas.
Para saber de qué sistema estamos hablando cuando vemos un número, a veces se le añade un pequeño número abajo a la derecha, llamado subíndice. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 101_{(2)} significa el número 101 en el sistema binario.
Tipos de sistemas de numeración
Los sistemas de numeración se pueden dividir en dos grandes grupos:
- Sistemas no posicionales: En estos sistemas, el valor de un símbolo no cambia sin importar dónde esté colocado en el número. Es como si cada símbolo siempre valiera lo mismo.
- Sistemas posicionales: Aquí, el valor de un símbolo depende de su posición dentro del número. Por ejemplo, en el número 222, el primer 2 vale 200, el segundo 2 vale 20 y el tercer 2 vale 2.
Por ejemplo, el sistema de numeración egipcio era no posicional. En cambio, el sistema que usaban los babilonios era posicional. La mayoría de los idiomas que hablamos hoy usan sistemas posicionales, casi siempre basados en grupos de 10 o 20.
Sistemas de numeración no posicionales: ¿Cómo contaban antes?
Estos son los sistemas más antiguos. Imagina que usabas tus dedos para contar hasta cinco, y luego decías "dos manos" para diez. También se sabe que se usaban cuerdas con nudos para registrar cantidades.
Algunos ejemplos famosos de sistemas no posicionales son:
- El sistema del antiguo Egipto.
- El sistema de numeración romana.
- Los sistemas usados por civilizaciones antiguas en América, como los mayas y los aztecas.
Los mayas, por ejemplo, tenían un sistema muy avanzado que usaba una base de 20. ¡Y lo más sorprendente es que ellos desarrollaron la idea del cero de forma independiente, mucho antes que en otros lugares del mundo! Hay inscripciones mayas con el cero que datan del año 36 antes de Cristo.
Sistemas de numeración posicionales: La base de nuestros números
En un sistema de numeración posicional, el número de símbolos que se pueden usar se llama la base del sistema. Si un sistema tiene una base b, significa que tiene b símbolos diferentes para escribir los números. Además, b unidades de un orden forman una unidad del siguiente orden superior.
El sistema decimal: Nuestro día a día
Nuestro sistema de numeración es el decimal, que tiene una base de 10. Esto significa que usamos 10 símbolos: del 0 al 9.
Piensa en cómo contamos:
- Cuando llegamos a 9, hemos usado todos los símbolos.
- Para seguir contando, añadimos una nueva "columna" a la izquierda (las decenas), ponemos a cero la columna de las unidades y seguimos contando. Así, después del 9 viene el 10.
- Cuando llegamos a 99, hemos usado todos los símbolos en dos columnas. Si sumamos 1, las unidades se ponen a cero y se suma 1 a las decenas. Pero las decenas también llegan a 9, así que se ponen a cero y se suma 1 a la siguiente columna (las centenas). Por eso, 99 + 1 = 100.
Es como el cuentakilómetros de un coche: cuando una rueda (una posición) llega al 9 y suma 1, vuelve a 0 y hace que la rueda de su izquierda avance un número. Estamos tan acostumbrados a esto que no nos damos cuenta de lo especial que es.
Además del decimal, existen otros sistemas posicionales muy importantes, como:
- El sistema binario (base 2), que solo usa 0 y 1. Es el lenguaje de las computadoras.
- El sistema octal (base 8).
- El sistema hexadecimal (base 16).
Los antiguos mayas también tuvieron un sistema de numeración posicional, aunque ya no se usa.
El Teorema Fundamental de la Numeración
Este teorema nos explica cómo se construye el valor de cualquier número en un sistema posicional. Es como una fórmula mágica para entender los números.
Imagina un número N en un sistema con base b. Cada dígito de ese número, dependiendo de su posición, se multiplica por la base elevada a una potencia. Luego, sumamos todos esos resultados.
Por ejemplo, en el sistema decimal (base 10), si tenemos el número 1492,36:
- El 1 está en la posición de los miles (10 elevado a 3).
- El 4 está en la posición de los cientos (10 elevado a 2).
- El 9 está en la posición de las decenas (10 elevado a 1).
- El 2 está en la posición de las unidades (10 elevado a 0).
- El 3 está en la posición de las décimas (10 elevado a -1).
- El 6 está en la posición de las centésimas (10 elevado a -2).
Así, el número 1492,36 se puede escribir como:
Esto es: 1000 + 400 + 90 + 2 + 0,3 + 0,06 = 1492,36.
Ejemplo en el sistema binario
Ahora veamos el sistema binario, que tiene base 2. Solo usa los símbolos {0, 1}. Aquí, dos unidades forman una unidad de orden superior.
Si contamos en binario:
- 0
- 1
- Después del 1, como solo tenemos 0 y 1, "agotamos" los símbolos. Así que añadimos una nueva columna y ponemos a cero la primera: 10 (que es 2 en decimal).
- Seguimos: 11 (que es 3 en decimal).
- Después del 11, si sumamos 1, las unidades se ponen a cero y se suma 1 a la siguiente columna. Pero esa columna también llega a su límite (1), así que se pone a cero y se suma 1 a la siguiente: 100 (que es 4 en decimal).
Así, en binario, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 11_{(2)} + 1_{(2)} = 100_{(2)} .
Un ejemplo: el número Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 111_{(2)} en binario.
- El primer 1 (de izquierda a derecha) está en la posición de
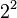(que es 4). - El segundo 1 está en la posición de
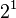(que es 2). - El tercer 1 está en la posición de
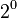(que es 1).
Entonces, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 111_{(2)} = 1 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = 4 + 2 + 1 = 7_{(10)} .
Véase también
En inglés: Numeral system Facts for Kids
- Sistema de numeración decimal
- Sistema de numeración octal
- Sistema hexadecimal
- Sistema duodecimal
- Sistema alfanumérico
- Base64
- Numeración romana
- Numeración egipcia
- Numeración maya
- Sistema sexagesimal
