Espacio métrico para niños
En matemática, un espacio métrico es como un conjunto de puntos donde podemos medir la distancia entre ellos. Imagina que tienes un mapa y quieres saber qué tan lejos está un lugar de otro. Un espacio métrico es una forma matemática de definir esa "distancia" de una manera muy precisa.
Para que un conjunto sea un espacio métrico, necesita tener una "función distancia" (o "métrica"). Esta función es una regla que nos dice la distancia entre cualquier par de puntos en ese conjunto. Además, esta regla debe cumplir ciertas propiedades, como las que esperamos de una distancia en la vida real.
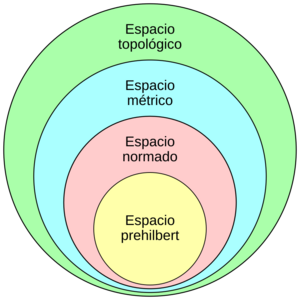
Un espacio métrico también es un tipo especial de espacio topológico. Esto significa que la forma en que medimos las distancias nos ayuda a entender cómo los puntos están "cerca" o "lejos" unos de otros, y cómo se forman las "regiones" o "vecindarios" en ese espacio.
El ejemplo más fácil de entender es el espacio tridimensional que conocemos, donde medimos las distancias con una regla. Otros ejemplos incluyen la superficie de una esfera (donde la distancia se mide a lo largo de la superficie curva) o el plano hiperbólico. A veces, la "distancia" no es física, sino más bien una forma de comparar cosas. Por ejemplo, la distancia de Hamming mide cuántos cambios necesitas hacer para transformar una palabra en otra.
Los espacios métricos son muy útiles en muchas áreas de las matemáticas porque nos permiten estudiar la "cercanía" y la "separación" de los objetos de una manera general.
Contenido
¿Qué es un espacio métrico?
Para entender mejor, piensa en la superficie de la Tierra como un conjunto de puntos. Podemos medir la distancia entre dos ciudades de varias maneras:
- La distancia más corta a lo largo de la superficie (como un avión o barco). Esto se llama distancia ortodrómica.
- La distancia en línea recta a través del interior de la Tierra. Esta es útil para entender cómo viajan las ondas sísmicas.
La idea de un espacio métrico es definir una distancia que sea flexible, pero que a la vez capture lo que intuitivamente entendemos por "distancia". Esto permite que los descubrimientos sobre espacios métricos se apliquen en muchos campos diferentes.
A veces, la métrica no mide una distancia física. Puede ser el "costo" de pasar de un estado a otro, o el "grado de diferencia" entre dos objetos. Por ejemplo, la distancia de Hamming entre dos cadenas de texto nos dice cuántos caracteres son diferentes.
La definición de un espacio métrico
Formalmente, un espacio métrico es un conjunto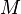 
(cuyos elementos llamamos puntos) junto con una función de distancia 
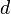(también llamada métrica). Esta función toma dos puntos de 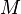y les asigna un número real, que es su distancia.
La función 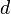debe cumplir las siguientes reglas para todos los puntos 
, 
, 
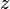en :
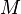- 1. La distancia es siempre positiva o cero:
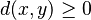
- La distancia entre dos puntos siempre es un número positivo o cero.
- Si la distancia entre e es cero, entonces e son el mismo punto (
). - Intuitivamente, no cuesta nada ir de un punto a sí mismo.
- 2. La distancia es simétrica:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d(x, y) = d(y, x)
- La distancia de a es la misma que la distancia de a .
- Esto significa que el camino de ida y el de vuelta miden lo mismo.
- 3. La desigualdad triangular:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d(x,z) \leq d(x,y) + d(y,z)
- La distancia directa entre dos puntos ( y 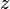) siempre es menor o igual que la distancia si pasas por un punto intermedio ().
- Imagina que vas de tu casa a la escuela. El camino directo es el más corto. Si pasas por la casa de un amigo, el camino será igual o más largo, ¡nunca más corto!
Cuando la métrica 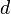es clara, a menudo decimos simplemente "el espacio métrico ".
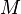Conceptos relacionados con un espacio métrico
En un espacio métrico Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (M, d) , podemos definir:
- Bola abierta: Es el conjunto de todos los puntos que están a una distancia menor que un cierto radio
de un punto central 
. Piensa en un círculo (en 2D) o una esfera (en 3D) sin incluir su borde. - Bola cerrada: Es similar a la bola abierta, pero incluye los puntos que están exactamente a la distancia del centro. Es decir, incluye su borde.
- Esfera: Es el conjunto de todos los puntos que están exactamente a la distancia de un punto central . Piensa en el borde de un círculo o la superficie de una esfera.
Historia de los espacios métricos
La idea de los espacios métricos fue introducida por el matemático Maurice Fréchet en 1906. Él quería estudiar funciones de una manera más general. Más tarde, Felix Hausdorff desarrolló y organizó estas ideas en su importante libro Principios de la teoría de conjuntos.
Desde entonces, los espacios métricos se han vuelto una parte fundamental de las matemáticas. Se usan en campos como la geometría diferencial y el análisis funcional. También son importantes en la Geometría fractal, que estudia formas complejas y "rugosas". En la informática, los espacios métricos finitos y discretos tienen muchas aplicaciones nuevas.
Ejemplos de espacios métricos
Aquí tienes algunos ejemplos para entender mejor:
- Métrica discreta: Imagina cualquier conjunto de puntos
. Definimos la distancia así: si dos puntos son iguales, su distancia es 0. Si son diferentes, su distancia es 1. ¡Es como si solo pudieras estar en el mismo lugar o en un lugar completamente diferente!
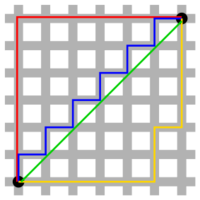
- Números reales y espacio euclídeo: Los números reales (la recta numérica) con la distancia usual Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): d(x,y)=|y-x| (el valor absoluto de la diferencia) forman un espacio métrico. De manera similar, el espacio euclídeo de 2 o 3 dimensiones (o más) con la distancia euclidiana (la que calculas con el teorema de Pitágoras) también son espacios métricos.
- Espacios vectoriales normados: Un espacio vectorial normado es un tipo de espacio donde puedes sumar "vectores" y multiplicarlos por números, y además tienen una "norma" (que es como una longitud). Si defines la distancia entre dos vectores como la norma de su diferencia, obtienes un espacio métrico.
- Funciones acotadas: Si tienes un conjunto de funciones que no crecen infinitamente, puedes definir la distancia entre dos funciones como la mayor diferencia entre sus valores en cualquier punto.
- Conjuntos compactos (distancia de Hausdorff): Puedes incluso medir la distancia entre dos conjuntos de puntos. La distancia de Hausdorff entre dos conjuntos nos dice qué tan cerca está cada punto de un conjunto de algún punto del otro conjunto.
Espacios metrizables
Un espacio topológico se llama metrizable si podemos encontrar una función de distancia que genere la misma "estructura de cercanía" que ya tiene ese espacio. Es como si el espacio ya tuviera una forma de entender la cercanía, y nosotros encontramos la regla de distancia que lo describe.
Los matemáticos estudian cuándo un espacio topológico puede ser metrizable. Hay varios teoremas que nos ayudan a saberlo, como el Teorema de metrización de Urysohn o el de Nagata-Smirnov.
Galería de imágenes
-
Diagrama que ilustra la distancia ortodrómica (en verde) y la distancia rectilínea (en rojo) entre dos puntos P y Q de una esfera.
Véase también
En inglés: Metric space Facts for Kids
