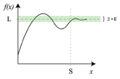
Límite (matemática) para niños
El límite en matemáticas es una idea muy importante que nos ayuda a entender cómo se comportan los números o las funciones cuando se acercan mucho a un punto específico. Imagina que estás caminando hacia una línea en el suelo. Puedes acercarte tanto como quieras a esa línea, pero quizás nunca la toques. El límite es como esa línea a la que te acercas.
Este concepto es fundamental en el cálculo, una rama de las matemáticas. Se usa para definir ideas como la convergencia (cuando algo se acerca a un valor), la continuidad (cuando una función no tiene "saltos"), la derivación (la tasa de cambio) y la integración (el área bajo una curva).
Para escribirlo de forma corta, usamos el símbolo 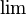 (que significa "límite"). Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim (a_n)=a significa que la secuencia
(que significa "límite"). Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim (a_n)=a significa que la secuencia 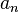 se acerca al valor
se acerca al valor  . También se puede usar una flecha, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_n\rightarrow a .
. También se puede usar una flecha, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_n\rightarrow a .
¿Qué es un Límite en Matemáticas?
El límite es una herramienta matemática que nos permite estudiar el comportamiento de una sucesión de números o de una función cuando sus valores se aproximan a un punto determinado. No se trata de lo que ocurre exactamente en ese punto, sino de lo que sucede "alrededor" de él, a medida que nos acercamos cada vez más.
La Historia de los Límites
La idea de límite no es nueva. Ya en la antigua Grecia, matemáticos como Euclides y Arquímedes usaban un método llamado "agotamiento". Con este método, calculaban áreas o volúmenes de figuras complejas. Lo hacían inscribiendo y circunscribiendo polígonos con cada vez más lados. Así, se acercaban más y más al valor real.
Grégoire de Saint-Vincent fue uno de los primeros en dar una definición de "límite" para una serie geométrica en 1647. Él dijo que el límite es el "final de la serie" al que se puede acercar mucho, pero nunca llegar.
La definición moderna y más precisa de límite, que usamos hoy, fue desarrollada por Bernard Bolzano en 1817. Más tarde, Augustin-Louis Cauchy en 1821 y Karl Weierstrass la formalizaron aún más. Esta es la famosa "definición épsilon-delta".
La forma en que escribimos los límites hoy, con la flecha debajo del símbolo, fue introducida por G. H. Hardy en su libro de 1908, Un curso de matemáticas puras.
Límite de una Sucesión: ¿Qué Significa?
Una sucesión es una lista ordenada de números. Por ejemplo, 1, 2, 3, 4... o 1/2, 1/4, 1/8, 1/16...
El límite de una sucesión nos dice si los números de esa lista se acercan a un valor específico a medida que avanzamos en la lista. Si se acercan a un número, decimos que la sucesión converge a ese número.
Ejemplo de Límite de una Sucesión
Imagina la sucesión de números: 1/2, 1/4, 1/8, 1/16, 1/32... Cada número es la mitad del anterior. Si sigues esta lista, los números se hacen cada vez más pequeños. Se acercan mucho a cero.
En este caso, el límite de la sucesión es 0. Esto se escribe así:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim_{n\to\infty}a_n = 0
Esto significa que, a medida que  (la posición en la lista) se hace muy grande, los términos
(la posición en la lista) se hace muy grande, los términos 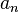 se acercan a 0.
se acercan a 0.
Si una sucesión no se acerca a ningún número específico, decimos que es divergente.
Límite de una Función: ¿Cómo Funciona?
El límite de una función es similar al de una sucesión. Aquí, vemos qué valor toma la función cuando su entrada (la "x") se acerca a un número determinado.
Por ejemplo, si tenemos una función  , y queremos saber qué pasa cuando
, y queremos saber qué pasa cuando  se acerca a un número
se acerca a un número  , buscamos el límite. Se escribe así:
, buscamos el límite. Se escribe así:
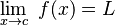
Esto significa que, a medida que  se acerca a
se acerca a  , el valor de la función
, el valor de la función  se acerca a
se acerca a 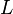 .
.
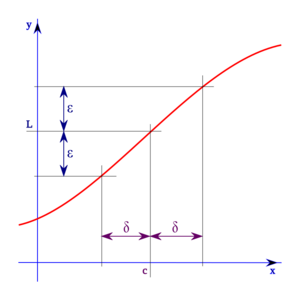
La Definición Épsilon-Delta Explicada
Para ser muy precisos, los matemáticos usan la "definición épsilon-delta". Suena complicado, pero la idea es simple: Si el límite de  cuando
cuando  se acerca a
se acerca a  es
es 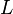 , significa que podemos hacer que
, significa que podemos hacer que  esté tan cerca de
esté tan cerca de 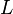 como queramos. Para lograrlo, solo necesitamos que
como queramos. Para lograrlo, solo necesitamos que  esté lo suficientemente cerca de
esté lo suficientemente cerca de  .
.
Imagina que  (épsilon) es una distancia muy pequeña que representa lo cerca que queremos que esté
(épsilon) es una distancia muy pequeña que representa lo cerca que queremos que esté  de
de 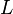 . La definición dice que siempre podemos encontrar una distancia
. La definición dice que siempre podemos encontrar una distancia 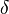 (delta) alrededor de
(delta) alrededor de  . Si
. Si  está dentro de esa distancia
está dentro de esa distancia 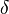 de
de  , entonces
, entonces  estará dentro de la distancia
estará dentro de la distancia  de
de 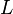 .
.
El Infinito como Límite: ¿Qué Pasa Cuando No Hay Fin?
A veces, una sucesión o función no se acerca a un número específico, sino que sus valores se hacen cada vez más grandes (o más pequeños). Decimos que "tiende al infinito".
Por ejemplo, la sucesión 1, 2, 3, 4, 5... no se acerca a un número. Sus valores crecen sin parar. En este caso, decimos que el límite es infinito. Se escribe: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lim_{n\rightarrow \infty} a_n = \infty Esto significa que, no importa cuán grande sea un número que elijas, la sucesión eventualmente lo superará.
Sucesiones Oscilatorias: Un Caso Especial
Algunas sucesiones no convergen a un número ni tienden al infinito. Por ejemplo, la sucesión -1, 1, -1, 1, -1... Esta sucesión salta entre -1 y 1. No se acerca a un solo valor. A estas sucesiones las llamamos oscilatorias.
Galería de imágenes
Véase también
 En inglés: Limit (mathematics) Facts for Kids
En inglés: Limit (mathematics) Facts for Kids
- Continuidad (matemáticas)
- Límite de una sucesión
- Límite de una función
- Asíntota
- Análisis asintótico: método para describir el comportamiento límite.
- Notación Big O: utilizada para describir el comportamiento límite de una función cuando el argumento tiende hacia un valor particular o hacia el infinito
- Límite de una función
- Límite unilateral: cualquiera de los dos límites de funciones de una variable real x, al acercarse x a un punto por arriba o por abajo.
- Lista de límites: lista de límites de funciones comunes
- Teorema de la compresión: encuentra el límite de una función por comparación con otras dos funciones



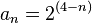 para
para  converge al valor 0, como se puede observar en la ilustración.
converge al valor 0, como se puede observar en la ilustración.