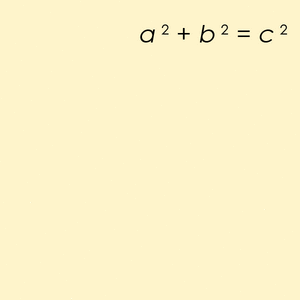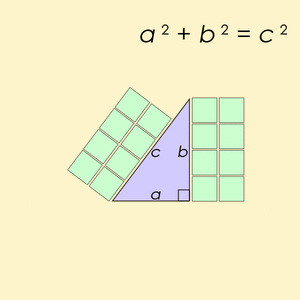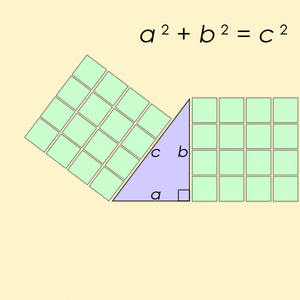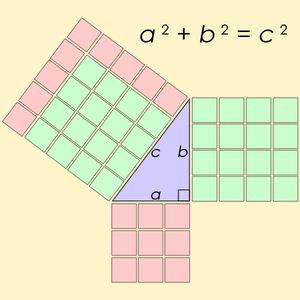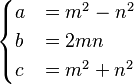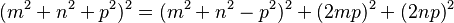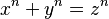Terna pitagórica para niños
Una terna pitagórica es un grupo de tres números enteros positivos (como 3, 4 y 5) que cumplen una regla especial: si elevas al cuadrado los dos números más pequeños y los sumas, el resultado es igual al cuadrado del número más grande. Esta regla se escribe así: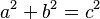 
.
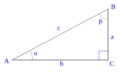
Estos números están muy relacionados con el teorema de Pitágoras. Este teorema dice que en cualquier triángulo rectángulo (un triángulo con un ángulo de 90 grados), el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados (los catetos). Si los lados de un triángulo rectángulo son números enteros, entonces forman una terna pitagórica. Y al revés, cualquier terna pitagórica puede formar los lados de un triángulo rectángulo.
Contenido
¿Qué son las Ternas Pitagóricas?
A los números enteros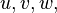 
que cumplen la ecuación 
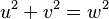, se les llama números pitagóricos.
Ternas Pitagóricas Primitivas
Las ternas pitagóricas se escriben como (a, b, c). Una terna es primitiva si sus tres números no tienen ningún divisor común aparte del 1. Es decir, son primos relativos entre sí.
Aquí tienes las primeras 16 ternas pitagóricas primitivas donde el número más grande (c) es menor o igual a 100:
| ( 3 , 4 , 5 ) | ( 5, 12, 13) | ( 8, 15, 17) | ( 7, 24, 25) |
| ( 9, 40, 41) | (11, 60, 61) | (12, 35, 37) | (13, 84, 85) |
| (16, 63, 65) | (20, 21, 29) | (28, 45, 53) | (33, 56, 65) |
| (36, 77, 85) | (39, 80, 89) | (48, 55, 73) | (65, 72, 97) |
Un Viaje por la Historia de las Ternas Pitagóricas
El estudio de las ternas pitagóricas es muy antiguo. Mucho antes de que naciera el famoso matemático Pitágoras (alrededor del 570 al 490 a.C.), ya se usaban en la Antigua Babilonia. Hace más de 3000 años, los babilonios usaban estas ternas para medir y delimitar terrenos. Incluso se han encontrado tablillas de arcilla, como la Plimpton 322, que muestran listas de estas ternas. Esto sugiere que tenían un método para encontrarlas.
También hay pruebas de que los antiguos egipcios las usaban para construir ángulos rectos, lo cual era muy útil en sus edificaciones. Pitágoras, por su parte, se interesó en encontrar soluciones enteras para la ecuación 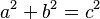. Él encontró una forma de generar infinitas ternas usando una fórmula.
Una fórmula común para generar ternas pitagóricas es:
donde m y n son números enteros positivos y m es mayor que n. Esta fórmula también aparece en los escritos del matemático griego Euclides.
Cómo se Generan y sus Características
Las ternas pitagóricas pueden ser de dos tipos: primitivas o no primitivas.
- Una terna es primitiva si el máximo común divisor de sus tres números es 1. Esto significa que no tienen factores comunes, excepto el 1.
- Si tienes una terna primitiva (a, b, c), puedes crear infinitas ternas no primitivas multiplicando cada número por un entero positivo d. Por ejemplo, si (3, 4, 5) es primitiva, (6, 8, 10) o (9, 12, 15) son no primitivas. Los triángulos formados por ternas no primitivas son siempre una versión más grande o más pequeña de un triángulo formado por una terna primitiva.
La fórmula que mencionamos antes:
- a = m² − n²
- b = 2mn
- c = m² + n²
genera una terna pitagórica si m > n son enteros positivos. Esta terna será primitiva si m y n no tienen factores comunes (son coprimos) y solo uno de ellos es un número par. Si ambos m y n fueran impares, los números a, b y c serían todos pares, y la terna no sería primitiva.
Es interesante saber que hay infinitas ternas pitagóricas primitivas. Además, a veces un mismo número puede ser parte de más de una terna primitiva. Por ejemplo, el número 20 es parte de (20, 21, 29) y (20, 99, 101).
Familias de Ternas Pitagóricas
Las ternas pitagóricas se pueden agrupar en "familias" según ciertas propiedades o relaciones entre sus números. Aquí te mostramos algunas de estas familias:
| Nombre de la familia | Propiedad | Ejemplos |
|---|---|---|
| Pitágoras | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c-b=1 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [5, 12, 13] [7, 24, 25] [9, 40, 41] |
| Platón | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c-b=2 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [15, 8, 17] [35,12, 37] [99, 20, 101] |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c-b=4 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [30, 16,34][70,24,74][126,32,130] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c-b=8 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [20,21,29] [28,45, 53][36,77, 85] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cfrac{c-3a}{2}=1 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [145,408,433] [840,2378,2522][4901,13860,14701] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cfrac{c-3a}{2}=2 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [287,816,865] [1683,4756,5045][9799,27720,29401] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c-2a=2 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [16,30,34] [240,418,482] [3360,5822,6722] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c-2a=3 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [5,12,13] [95,168,193][1349,2340,2701] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2a-c=1 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [33,56,65] [451,780,901][6273,10864,12545] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |3a-2c|=4 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [96,110,146][1768,1974,2650] [31680,35422,47522] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |3a-2c|=1 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [65,72,97] [1155,1292,1733][20737,23184,31105] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |3a-2c|=5 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [21,20,29] [319,360,481][5781,6460,8669] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |\cfrac{b}{2}-a|=1 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [5,12,13] [39,80,89] [272,546,610] | |
| Fermat | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |b-a|=1 | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [696,697,985] [4059,4060,5741] [23660,23661,33461] |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |\cfrac{3b}{2}-a| \in \{1,3,9\} | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [91,60,109] [15,8,17][819,540,981] | |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |2b-a| \in \{1,4,5\} | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): [273,136,305] [416,210,466] [1363,684,1525] |
Más allá de las Ternas: Cuádruplas y el Último Teorema de Fermat
Cuádruplas Pitagóricas
Así como las ternas pitagóricas se relacionan con triángulos, también podemos encontrar grupos de cuatro números que cumplen una regla similar. Es posible que el cuadrado de un número sea igual a la suma de los cuadrados de otros tres números. Esto se puede usar para calcular la diagonal de una caja rectangular (un paralelepípedo) si sus lados son números enteros.
La fórmula para esto es:
Algunos ejemplos son:
(9 = 4 + 4 + 1)
(169 = 9 + 16 + 144)
El Último Teorema de Fermat
El último teorema de Fermat es una idea muy famosa en matemáticas. Fue propuesta por Pierre de Fermat alrededor de 1637. Este teorema dice que, a diferencia de las ternas pitagóricas (donde el exponente es 2), no existen soluciones con números naturales para la ecuación:
si el exponente n es mayor que 2. Es decir, no puedes encontrar tres números enteros positivos x, y, z que cumplan esta ecuación si n es 3, 4, 5, o cualquier número entero mayor que 2.
Este teorema fue un misterio por más de 300 años. Muchos matemáticos intentaron demostrarlo, pero nadie lo logró hasta 1995, cuando Andrew Wiles finalmente lo demostró usando matemáticas muy avanzadas.
Galería de imágenes
-
Triángulo rectángulo con sus tres lados y ángulos nombrados. El triángulo rectángulo cuyas longitudes de sus tres lados sean números enteros positivos, estos forman una terna pitagórica, y evidentemente
Véase también
En inglés: Pythagorean triple Facts for Kids
- Teorema de Pitágoras
- Número primo pitagórico
- Último teorema de Fermat
Enlaces externos
- Weisstein, Eric W. «Pythagorean Triple». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. Ofrece una discusión extensa sobre las ternas pitagóricas.
- Calculadora Javascript con las fórmulas para generar ternas (en inglés).
- Monografías sobre números y elementos.
