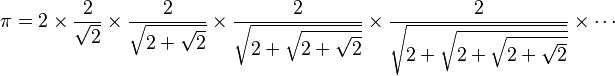François Viète para niños
Datos para niños François Viète |
||
|---|---|---|
 |
||
| Información personal | ||
| Nacimiento | 1540 Fontenay-le-Comte (Poitou, Reino de Francia) |
|
| Fallecimiento | 23 de febrero de 1603 París (Reino de Francia) |
|
| Nacionalidad | Francesa | |
| Educación | ||
| Educación | Grado en Leyes | |
| Educado en | Universidad de Poitiers (1558-1559) | |
| Información profesional | ||
| Ocupación | Matemático, criptógrafo y abogado (desde 1571) | |
| Área | Álgebra, criptografía, geometría y matemáticas | |
| Empleador |
|
|
| Alumnos | Marino Ghetaldi y Alexander Anderson | |
| Obras notables |
|
|
| Firma | ||
 |
||
François Viète (cuyo nombre en latín era Franciscus Vieta) fue un importante matemático y abogado francés. Nació en Fontenay-le-Comte en 1540 y falleció en París en 1603.
Se le considera una figura clave en el desarrollo del álgebra. Fue el primero en usar letras para representar los números desconocidos en las ecuaciones. También fue muy hábil en criptografía, lo que le permitió descifrar mensajes secretos.
Viète fue un consejero de confianza para los reyes de Francia, Enrique III y Enrique IV. Era muy respetado por su lealtad y sus habilidades.
Contenido
La vida de François Viète
Sus primeros años y estudios
François Viète era hijo de un procurador, una especie de abogado. Estudió derecho en la Universidad de Poitiers. En 1560, comenzó a trabajar como abogado en su ciudad natal, Fontenay-le-Comte.
Se le encargaron casos importantes, como la administración de propiedades de la viuda del rey Francisco I de Francia. También trabajó para María Estuardo, la reina de Escocia.
Al servicio de familias importantes
En 1564, Viète empezó a trabajar para la familia Soubise como secretario personal. También fue maestro de Catherine de Parthenay, con quien mantuvo una amistad durante toda su vida.
Gracias a su trabajo, conoció a personas influyentes de la nobleza. Entre ellos estaban Gaspar de Coligny y Enrique I de Borbón-Condé. También conoció a Juana de Albret, reina de Navarra, y a su hijo, Enrique de Navarra, quien más tarde sería el rey Enrique IV de Francia.
Su carrera al servicio del rey
En 1571, Viète se convirtió en abogado del Parlamento de París. En 1573, fue nombrado consejero en el Parlamento de Rennes.
En 1576, el rey Enrique III de Francia lo contrató para misiones especiales. Para 1580, Viète ya trabajaba exclusivamente para el rey en el Parlamento de París.
En 1580, Viète manejó un caso importante entre el duque de Nemours y Françoise de Rohan. El fallo fue a favor de Françoise, lo que le ganó la enemistad de un grupo político. Por esta razón, en 1584, fue apartado de sus funciones.
Durante este tiempo, el futuro rey Enrique IV escribió varias cartas pidiendo que Viète recuperara su puesto. Sin embargo, no fue escuchado. Viète aprovechó estos años para dedicarse por completo a las matemáticas.
En 1589, tras algunos conflictos en París, el rey Enrique III tuvo que refugiarse en Blois. Pidió a sus funcionarios que se reunieran con él en Tours. Viète fue uno de los primeros en responder a este llamado.
Después de la muerte de Enrique III, Viète se unió al consejo privado de Enrique IV. El nuevo rey admiraba mucho el talento matemático de Viète. A partir de 1594, Viète se dedicó principalmente a descifrar códigos secretos de los enemigos, una tarea que ya realizaba desde 1580.
En 1590, Enrique IV hizo pública una carta que Viète había descifrado. Esta carta revelaba que un líder importante en Francia quería ser rey en lugar de Enrique IV. La publicación de esta información fue muy importante en ese momento.
Viète dejó de trabajar para el rey en 1602 debido a una enfermedad y falleció en 1603. Poco antes de morir, escribió un documento sobre criptografía que hizo que los métodos de cifrado de su época quedaran anticuados.
Contribuciones matemáticas de Viète
La "logística especiosa": el álgebra con símbolos
En la época de Viète, los matemáticos se inspiraban mucho en la geometría griega. El álgebra se veía más como un conjunto de reglas para calcular. Algunos matemáticos usaban la geometría para entender el álgebra.
Viète propuso algo diferente: usar el álgebra para resolver problemas de geometría. A partir de 1591, comenzó a publicar su propia teoría matemática. La llamó "logística especiosa", que significa el arte de calcular usando símbolos. Esto era diferente de la "logística numerosa", que era el cálculo con números.
La "logística especiosa" de Viète tenía tres pasos:
- Primero, se anotaban todas las cantidades conocidas y desconocidas usando símbolos especiales que él creó. Luego, el problema se escribía como una ecuación. A esto lo llamó zetética. Las cantidades conocidas se representaban con consonantes (como B, D) y las desconocidas con vocales (como A, E).
- El segundo paso, el análisis porístico, permitía transformar y analizar la ecuación. Se buscaba una relación clave, llamada porisma, para avanzar al siguiente paso.
- Finalmente, en el análisis rético, se volvía al problema original y se encontraba una solución usando una construcción geométrica basada en el porisma.
Con este método, Viète logró resolver completamente ecuaciones de segundo grado (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax^2 + bx = c ) y de tercer grado (como 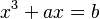 ).
).
El impacto de su álgebra con símbolos
La "logística especiosa" de Viète no fue adoptada de inmediato por todos. Sus símbolos matemáticos eran un poco complicados. Además, no separaba claramente el álgebra de la geometría, lo que hacía que los problemas complejos fueran difíciles de resolver. Su álgebra fue superada más tarde por la geometría analítica de Descartes.
Sin embargo, Viète fue el primero en usar letras para representar no solo las incógnitas, sino también los datos conocidos de un problema. También descubrió la relación entre las soluciones de una ecuación (llamadas raíces) y los números que aparecen en ella (llamados coeficientes).
La gran idea de Viète fue mostrar lo útil que era el álgebra y tratar de explicar sus métodos de forma organizada. Él creía firmemente que con el álgebra se podrían resolver todos los problemas.
El desafío de Adriano Romano
Viète participó en varias discusiones científicas. Una de las más famosas ocurrió con un matemático holandés llamado Adrianus Romanus. Romanus había escrito un libro con un problema muy difícil y mencionaba a todos los matemáticos importantes de Europa, pero no incluyó a ningún francés.
Cuando un embajador holandés se reunió con el rey Enrique IV, el rey le preguntó si conocía a algún matemático francés. El embajador respondió que no, porque Romanus no había mencionado a ninguno. El rey entonces llamó a Viète.
Viète resolvió el problema de Romanus en muy poco tiempo, escribiendo dos soluciones con un lápiz. Más tarde, envió muchas más soluciones, explicando que el problema tenía infinitas respuestas.
El problema de Romanus era una ecuación muy compleja. Viète se dio cuenta de que la solución estaba relacionada con un ángulo. En 1595, Viète publicó su respuesta a Romanus.
Viète le propuso a Romanus resolver un problema antiguo: encontrar un círculo que toque a otros tres círculos dados. Romanus propuso una solución, pero Viète no la consideró adecuada porque esperaba una solución usando solo una regla y un compás.
En el año 1600, Viète publicó su propia solución en un libro llamado Apollonius Gallus. Explicó que el número de soluciones dependía de cómo estuvieran colocados los tres círculos. Esta solución tuvo un gran impacto en Europa y le ganó la admiración de muchos matemáticos.
Más tarde, Adriano Romano visitó a Viète, y se hicieron buenos amigos. El trabajo completo de Viète fue publicado después de su muerte en 1607.
Otros descubrimientos de Viète
En 1593, Viète publicó un libro donde abordó problemas como la división de un ángulo en tres partes iguales (que está relacionado con una ecuación de tercer grado) y la construcción de figuras geométricas.
Ese mismo año, usando sus conocimientos de geometría y trigonometría, descubrió la primera fórmula infinita en la historia de las matemáticas para calcular el valor de pi:
También calculó el valor de pi con 10 decimales exactos. Para ello, usó un método similar al de Arquímedes, utilizando un polígono con muchísimos lados (393.216).
Lugares y conceptos con su nombre
- El cráter lunar Vieta fue nombrado en su honor.
- El asteroide (31823) Viète también lleva su nombre.
- El salto de Vieta es un método para resolver ciertos tipos de ecuaciones.
Galería de imágenes
Véase también
 En inglés: François Viète Facts for Kids
En inglés: François Viète Facts for Kids