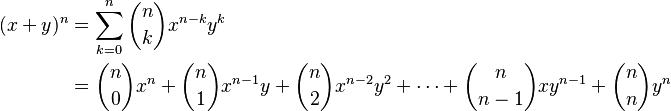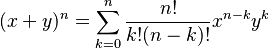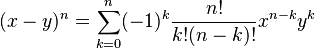Teorema del binomio para Niños

En matemáticas, el teorema del binomio es una regla especial que nos ayuda a expandir o "desplegar" expresiones como (x+y) elevadas a una potencia, por ejemplo, (x+y)². Imagina que tienes una suma de dos términos, como (x+y), y quieres multiplicarla por sí misma varias veces. Este teorema te da una fórmula para encontrar el resultado de manera más sencilla, sin tener que hacer todas las multiplicaciones paso a paso.

La fórmula nos dice que al expandir (x+y) elevado a una potencia entera positiva (como 2, 3, 4, etc.), el resultado será una suma de varios términos. Cada uno de estos términos tendrá una parte de 'x' y una parte de 'y' elevadas a diferentes potencias, y un número especial llamado "coeficiente" que los acompaña. Estos coeficientes se pueden encontrar usando el famoso Triángulo de Pascal.

Imagen del triángulo de Pascal.

Contenido

¿Qué dice el Teorema del Binomio?
- Ejemplos Sencillos del Teorema
Historia del Teorema del Binomio
Aplicaciones del Teorema del Binomio
- Identidades de Ángulos Múltiples
- La Serie para el Número 'e'
Galería de imágenes
Véase también

¿Qué dice el Teorema del Binomio?

Este teorema nos muestra cómo cualquier potencia de un binomio (una expresión con dos términos, como $x+y$ ) puede convertirse en una suma de términos. Si $x$ e $y$ no son cero, la fórmula general es:

\begin{align} (x+y)^n &=\sum_{k=0}^n {n \choose k}x^{n-k} y^k \\ &={n \choose 0}x^n + {n\choose 1} x^{n-1} y+{n\choose 2}x^{n-2}y^2 + \cdots + {n\choose n-1}xy^{n-1} + {n\choose n} y^n \end{align}

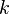Aquí, el símbolo $\binom{n}{k}$ se llama coeficiente binomial. Este número nos dice de cuántas maneras diferentes podemos elegir $k$ elementos de un grupo de $n$ elementos. Es como contar las combinaciones posibles.

Para calcular este coeficiente, usamos la siguiente fórmula, que incluye el factorial de un número (por ejemplo, 5! es 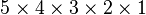$5 \times 4 \times 3 \times 2 \times 1$ ):

(x+y)^n = \sum_{k=0}^n \frac{n!}{k!(n-k)!} x^{n-k} y^k

Si en lugar de una suma tenemos una resta, como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x-y)^n , la fórmula es muy parecida. Solo que los signos de los términos se alternan:

(x-y)^n = \displaystyle \sum_{k=0}^n (-1)^k\frac{n!}{k!(n-k)!} x^{n-k} y^k

Ejemplos Sencillos del Teorema

Para entenderlo mejor, veamos algunos ejemplos de cómo se expanden los binomios usando los coeficientes que encontramos en el Triángulo de Pascal:

Para $n=2$ :

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x + y)^2 = x^2 + 2xy + y^2 (Esto es lo mismo que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x+y) \times (x+y) )

Para $n=3$ :

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x + y)^3 = x^3 + 3 x^2 y + 3 x y^2 + y^3

Para $n=4$ :

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x + y)^4 = x^4 + 4 x^3 y + 6 x^2 y^2 + 4 x y^3 + y^4

Para $n=5$ :

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x + y)^5 = x^5 + 5 x^4 y + 10 x^3 y^2 + 10 x^2 y^3 + 5 x y^4 + y^5

Puedes ver cómo los números (coeficientes) en cada expansión coinciden con los números en las filas del Triángulo de Pascal.

Historia del Teorema del Binomio

Aunque a menudo se asocia con Isaac Newton, el teorema del binomio fue descubierto mucho antes. El matemático persa Al-Karaŷí lo encontró alrededor del año 1000.

Newton, en los años 1664 y 1665, mientras estaba en su casa en Lincolnshire, llevó este teorema un paso más allá. Él descubrió cómo aplicar la fórmula incluso cuando el exponente ( $n$ ) no era un número entero positivo, sino un número racional (como una fracción) o un número negativo. En estos casos, la expansión del binomio se convierte en una serie infinita de términos.

Newton usó una forma especial del Triángulo de Pascal, que había sido presentada por el matemático alemán Michael Stifel. Newton extendió esta tabla hacia arriba, descubriendo patrones que le permitieron calcular los coeficientes para exponentes negativos y fraccionarios.

Por ejemplo, para Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n=-1 , los coeficientes son Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1, -1, 1, -1, 1, -1, \ldots . Para 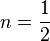$n=\frac{1}{2}$ , los coeficientes son Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1, \frac{1}{2}, -\frac{1}{8}, \frac{1}{16}, \ldots .

Newton se dio cuenta de que podía trabajar con estas series infinitas de la misma manera que con las expresiones finitas. Aunque Newton no publicó este teorema de inmediato, John Wallis lo hizo por primera vez en 1685 en su libro de Álgebra, dándole crédito a Newton por el descubrimiento.

El caso más simple del teorema del binomio, para $n=2$ , ya se conocía desde la época de Euclides (alrededor del año 300 a.C.). El término "coeficiente binomial" fue introducido por Stifel.

Aplicaciones del Teorema del Binomio

El teorema del binomio tiene muchas aplicaciones en diferentes áreas de las matemáticas y la ciencia.

Identidades de Ángulos Múltiples

En el mundo de los números complejos, el teorema del binomio se puede combinar con la Fórmula de De Moivre para encontrar fórmulas que relacionan los ángulos múltiples en trigonometría. Por ejemplo, nos ayuda a entender cómo Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos(2x) o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen(2x) se relacionan con 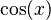$\cos(x)$ y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen(x) .

Por ejemplo, sabemos que: 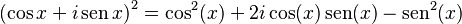$\left(\cos x+i\sen x\right)^2 = \cos^2(x) + 2i \cos(x)\sen (x) - \sen^2(x)$

Al comparar esto con la fórmula de De Moivre, podemos ver que: 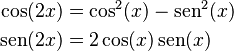$\begin{align} \cos(2x)&=\cos^2(x)-\sen^2(x) \\ \sen(2x)&= 2 \cos(x)\sen(x) \end{align}$ Estas son las conocidas fórmulas del ángulo doble.

La Serie para el Número 'e'

El número $e$ (un número muy importante en matemáticas, aproximadamente 2.71828) se puede definir de varias maneras. Una de ellas es usando un límite: 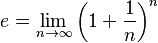$e = \lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^n$

Si aplicamos el teorema del binomio a la expresión Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left(1 + \frac{1}{n}\right)^n , y luego vemos qué pasa cuando $n$ se hace muy, muy grande (tiende a infinito), obtenemos una serie infinita para 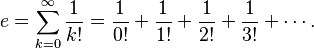$e$ : $e=\sum_{k=0}^\infty\frac{1}{k!}=\frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots.$ Esto significa que podemos calcular el valor de $e$ sumando los términos de esta serie.

Galería de imágenes

Imagen del triángulo de Pascal.

Véase también

En inglés: Binomial theorem Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Teorema_del_binomio&oldid=5004273»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Teorema del binomio para Niños. Enciclopedia Kiddle.

Teorema del binomio para niños