Geometría de Riemann para niños

En geometría diferencial, la geometría de Riemann es una rama de las matemáticas que estudia espacios especiales llamados variedades diferenciales. Imagina que estos espacios son como superficies curvas, pero que pueden tener muchas dimensiones.

En la geometría de Riemann, a cada punto de estos espacios se le asigna una forma especial que permite medir cosas como ángulos, longitudes de curvas y volúmenes de forma local. A partir de estas medidas pequeñas, se pueden calcular otras más grandes usando la integración.

Esta idea fue propuesta por primera vez por el matemático Bernhard Riemann en el siglo XIX. Incluye geometrías como la geometría euclidiana (la que aprendemos en la escuela, sobre planos y espacios rectos) y las geometrías no euclidianas, como la geometría elíptica y la geometría hiperbólica. Todas estas geometrías se estudian bajo el mismo enfoque, incluso si sus propiedades cambian de un punto a otro.

Cualquier espacio diferenciable puede tener una estructura de geometría de Riemann. Esta estructura extra es muy útil para resolver problemas en topología diferencial, que es el estudio de las propiedades de las formas que no cambian cuando se estiran o doblan. También es una base importante para entender las variedades pseudo-Riemann, que son fundamentales en la relatividad general, una teoría muy importante en la física.

¿Qué es la Geometría de Riemann?

Bernhard Riemann, el matemático que propuso esta geometría.

La geometría de Riemann fue presentada por Bernhard Riemann en el siglo XIX. Se encarga de estudiar una gran variedad de geometrías. En estas geometrías, las propiedades de medida pueden cambiar de un punto a otro. Esto incluye las geometrías no euclidianas que son diferentes a la geometría plana que conocemos.

Cualquier espacio suave puede tener una métrica de Riemann. Esta métrica es una herramienta matemática que ayuda a resolver problemas de topología diferencial. También es un paso importante para entender estructuras más complejas. Un ejemplo son las variedades pseudo-riemannianas. Estas son clave en la relatividad general, especialmente en cuatro dimensiones.

Existen otras extensiones de la geometría de Riemann, como la geometría de Finsler. Hay una conexión interesante entre la geometría diferencial y la forma en que se presentan los defectos en los cristales. Las imperfecciones en los cristales pueden causar torsiones y curvaturas.

Para entender mejor, puedes buscar información sobre:

• Tensor métrico
• Variedad de Riemann
• Curvatura

Historia de la Geometría de Riemann

El Nacimiento de una Nueva Geometría

Durante muchos siglos, la geometría euclidiana fue la única forma de entender el espacio. Los intentos de probar el postulado de las paralelas (una regla de la geometría euclidiana) llevaron a los matemáticos a pensar más allá. Así, Nikolai Lobachevski en 1829 y János Bolyai en 1832 crearon las primeras geometrías no euclidianas. Los espacios que ellos describieron, con geometría hiperbólica, ahora se ven como casos especiales de las variedades de Riemann con "curvatura negativa".

Antes de ellos, Carl Friedrich Gauss estudió la geometría diferencial de superficies. Él introdujo la curvatura de Gauss, una medida fundamental. Gauss descubrió que esta curvatura se podía calcular solo con la información de la superficie, sin importar cómo estuviera en el espacio. A esto lo llamó su "teorema notable".

El verdadero inicio de la geometría de Riemann se dio con Bernhard Riemann en el siglo XIX. En una famosa conferencia, él generalizó la geometría de superficies de Gauss a cualquier número de dimensiones. Esto expandió mucho la idea de geometría no euclidiana. Sin embargo, tomó varias décadas desarrollar completamente este nuevo concepto.

Hacia una Formalización Completa

La segunda mitad del siglo XIX se dedicó a entender mejor la geometría hiperbólica. Se crearon diferentes modelos para representarla, que luego fueron útiles en la relatividad especial. Surgieron herramientas importantes, como la teoría de grupos de Lie en la década de 1870. Felix Klein destacó la importancia de los grupos en geometría con su programa de Erlangen.

Un paso crucial fue cuando Gregorio Ricci-Curbastro y Tullio Levi-Civita desarrollaron el cálculo tensorial en 1900. Aunque el concepto de "espacio" aún no estaba claro, los cálculos con tensores avanzaron mucho. Esta herramienta fue muy importante cuando Albert Einstein la usó en su teoría de la relatividad general en 1916.

Desde 1902 hasta los años 30, se intentó definir formalmente la idea de variedad diferenciable. Esto se logró con el Teorema de inmersión de Whitney en 1936. Finalmente, la geometría de Riemann tuvo un marco claro para su estudio.

Un Campo de Investigación en Crecimiento

Mijaíl Grómov, ganador del Premio Abel en 2009 por sus importantes aportaciones a la geometría.

Grigori Perelman usó la geometría de Riemann para resolver la famosa conjetura de Poincaré en topología.

La clasificación de espacios simétricos por Élie Cartan en 1926 fue un resultado clave. En los años 30, aparecieron los primeros teoremas sobre variedades con curvatura positiva.

El teorema de la esfera en 1960 marcó un punto alto para las ideas clásicas. Luego, la geometría de Riemann tuvo un resurgimiento. Se desarrollaron métodos de geometría espectral, inspirados en la pregunta de Mark Kac: "¿Se puede oír la forma de un tambor?". En los años 80, Mijaíl Grómov introdujo una forma de medir la distancia entre variedades de Riemann.

Al mismo tiempo, Richard Hamilton comenzó a estudiar el "flujo de Ricci". Esto llevó a un programa para demostrar resultados de topología usando la geometría de Riemann. Este programa fue muy exitoso, con la demostración de la conjetura de Poincaré por Grigori Perelman en 2003.

Conceptos de la geometría de Riemann, como la curvatura, se usan ahora en muchos otros campos. Grómov definió los espacios CAT(k). También se usan en la teoría geométrica de grupos.

Conceptos Básicos de la Geometría de Riemann

¿Qué son las Geodésicas?

Los grandes círculos en una esfera son ejemplos de geodésicas.

Una geodésica en un elipsoide, mostrando un camino complejo.

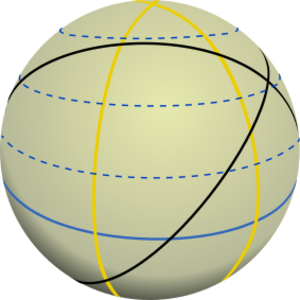
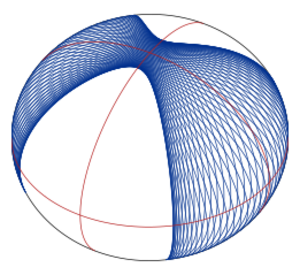
Las geodésicas son como las líneas rectas en el espacio euclidiano. Nos ayudan a encontrar los caminos más cortos entre dos puntos. Sin embargo, en espacios curvos, sus propiedades son más complejas. Hay que diferenciar entre lo que pasa cerca de un punto y lo que pasa a nivel global.

Las geodésicas se definen usando el cálculo de variaciones. Si tomas dos puntos, las geodésicas son las curvas que minimizan la longitud entre ellos. También se pueden ver como "bandas elásticas" estiradas sobre la superficie.

Por ejemplo, en una esfera, las geodésicas son los grandes círculos. Esto muestra que una geodésica no siempre es el camino más corto. Puedes ir de un punto a otro por el arco más corto o el más largo de un gran círculo.

Pero, si miras de cerca, la situación es más simple. Las geodésicas son "localmente minimizadoras". Esto significa que, entre dos puntos muy cercanos en una geodésica, el camino es el más corto. Desde un punto dado, solo hay una geodésica con una dirección inicial específica.

En un espacio completo y conectado, las geodésicas pueden extenderse indefinidamente. Además, entre dos puntos siempre hay al menos una geodésica que es el camino más corto. Esto se conoce como el teorema de Hopf-Rinow.

¿Qué es la Curvatura?

Un triángulo en una superficie con curvatura negativa, donde la suma de sus ángulos es menor a 180 grados.

En la geometría de Riemann, aunque las geodésicas son como líneas rectas, las medidas de longitudes, ángulos y áreas pueden ser diferentes. Por ejemplo, la suma de los ángulos de un triángulo en geometría euclidiana es 180 grados. La curvatura nos ayuda a medir estas diferencias.

En superficies en el espacio tridimensional, la curvatura se llama curvatura de Gauss. Se mide en cada punto. Si la curvatura es positiva, la superficie se parece a una esfera. Si es negativa, se parece a una silla de montar. Un resultado importante de Gauss dice que la curvatura se puede calcular solo con la información de la superficie, sin importar cómo esté "incrustada" en el espacio.

De forma más general, en cualquier variedad de Riemann, se puede construir un objeto complejo llamado Tensor de curvatura de Riemann. Este tensor es complicado, pero al simplificarlo, obtenemos el tensor de curvatura de Ricci y la curvatura escalar. Estos objetos contienen información importante sobre la curvatura.

Una forma de entender la curvatura es a través de la curvatura seccional. Esta es la curvatura de Gauss de las superficies formadas por las geodésicas en diferentes direcciones. Una curvatura seccional positiva significa que las geodésicas tienden a acercarse. Una curvatura negativa significa que tienden a alejarse.

¿Qué son los Operadores de Derivación?

Transporte paralelo de un vector a lo largo de una curva cerrada en una esfera. El vector cambia de dirección debido a la curvatura.

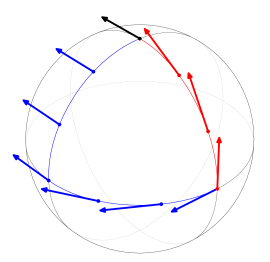
Dos ideas técnicas relacionadas con la curvatura y las geodésicas son la conexión afín y el transporte paralelo. Estos son métodos para conectar vectores que están en diferentes puntos del espacio. También permiten "derivar" campos vectoriales.

En un espacio diferencial general, no hay una forma única de hacer esto. Por ejemplo, no se puede definir el vector de aceleración de una curva en el espacio.

Lo sorprendente de las variedades de Riemann es que existe una conexión especial asociada a la métrica, llamada conexión Levi-Civita. Esta conexión es única y permite mantener la estructura euclidiana al conectar los espacios tangentes. Esto es un pilar fundamental de la geometría de Riemann. Usando la conexión Levi-Civita, se puede transportar un vector a lo largo de una curva.

El tensor de curvatura de Riemann se define a partir de la conexión Levi-Civita. La curvatura se puede ver como la medida de cuánto "gira" un vector si se transporta a lo largo de un camino cerrado y regresa al punto de partida.

También se puede crear una versión generalizada del Laplaciano para la geometría de Riemann, llamado operador de Laplace-Beltrami.

Teoremas Importantes en la Geometría de Riemann

Aquí hay algunos de los teoremas más conocidos y bellos de la geometría de Riemann:

Teoremas Generales

• Teorema de Gauss-Bonnet: Este teorema dice que la integral de la curvatura de Gauss en una superficie compacta de 2 dimensiones es igual a un valor relacionado con la característica de Euler de la superficie.
• Teorema de inmersión de Nash (también llamado Teorema Fundamental de la geometría de Riemann): Este teorema establece que cualquier variedad de Riemann puede ser "incrustada" de forma isométrica en un espacio euclidiano de mayor dimensión.

Geometría a Gran Escala

Estos teoremas asumen ciertas propiedades locales del espacio (generalmente relacionadas con la curvatura) para entender la estructura global del espacio. Esto incluye información sobre la forma topológica de la variedad o el comportamiento de los puntos a grandes distancias.

Curvatura Seccional con Límites

• Teorema de la esfera. Si un espacio de Riemann compacto y simplemente conectado tiene una curvatura seccional entre 1/4 y 1, entonces es similar a una esfera.
• Teorema de finitud de Cheeger. Con ciertas constantes, solo hay un número limitado de variedades de Riemann compactas con curvatura seccional, diámetro y volumen específicos.
• Variedades casi planas de Grómov. Si una variedad de Riemann tiene una curvatura seccional muy pequeña y un diámetro limitado, entonces su "cubierta finita" es similar a una variedad nula.

Curvatura Seccional con Límite Inferior

• El teorema del alma de Cheeger-Gromoll. Si un espacio de Riemann no compacto y completo tiene curvatura no negativa, contiene una subvariedad compacta llamada "alma". Si la curvatura es siempre positiva, el espacio es similar a un espacio euclidiano.
• Teorema del número de Betti de Grómov. Existe un límite para la suma de los números de Betti de una variedad de Riemann compacta con curvatura de sección positiva.
• Teorema de finitud de Grove-Petersen. Con ciertas constantes, solo hay un número limitado de tipos de homotopía de variedades de Riemann compactas con curvatura seccional, diámetro y volumen específicos.

Curvatura Seccional con Límite Superior

• El teorema de Cartan–Hadamard dice que un espacio de Riemann completo y simplemente conectado con curvatura seccional no positiva es similar a un espacio euclídeo. Esto significa que dos puntos cualesquiera están unidos por una única geodésica.
• El flujo geodésico de cualquier espacio de Riemann compacto con curvatura seccional negativa es ergódico (se comporta de manera uniforme a lo largo del tiempo).
• Si un espacio de Riemann completo tiene curvatura seccional limitada por una constante negativa, entonces es un Espacio CAT(k). Esto tiene muchas implicaciones para su grupo fundamental:

• Se puede describir con un número finito de elementos.
• El problema de saber si dos palabras son iguales en el grupo tiene una solución.
• Contiene un número finito de clases de elementos de orden finito.
• Sus subgrupos abelianos son virtualmente cíclicos.

Curvatura de Ricci con Límite Inferior

• Teorema de Myers. Si un espacio de Riemann completo tiene curvatura de Ricci positiva, entonces su grupo fundamental es finito.
• Fórmula de Bochner. Si un espacio de Riemann compacto tiene curvatura de Ricci no negativa, su primer número de Betti es como máximo su dimensión.
• Teorema de la división. Si un espacio de Riemann completo tiene curvatura de Ricci no negativa y una "línea recta" (geodésica que minimiza la distancia), entonces es como el producto de una línea real y otro espacio de Riemann.
• Desigualdad de Bishop-Grómov. El volumen de una esfera en un espacio de Riemann completo con curvatura de Ricci positiva es como máximo igual al volumen de una esfera del mismo radio en el espacio euclidiano.
• Teorema de la compacidad de Grómov. El conjunto de todas las variedades de Riemann con curvatura de Ricci positiva y diámetro limitado es "precompacto" en la métrica de Grómov-Hausdorff.

Curvatura de Ricci Negativa

• La isometría de una variedad de Riemann compacta con curvatura de Ricci negativa es discreta.
• Cualquier espacio suave de dimensión 3 o más puede tener una métrica de Riemann con curvatura de Ricci negativa. (Esto no es cierto para superficies).

Curvatura Escalar Positiva

• Un toro (forma de rosquilla) de n dimensiones no puede tener una métrica con curvatura escalar positiva.
• Si el radio de inyectividad de una variedad de Riemann compacta es grande, entonces la curvatura escalar media tiene un límite superior.

Ver También

• Anexo:Glosario de la geometría de Riemann
• Élie Cartan
• Heinz Hopf
• Pável Aleksándrov
• Víktor Toponógov

Enlaces Externos

• Weisstein, Eric W. «Riemannian Geometry». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

Véase también

En inglés: Riemannian geometry Facts for Kids