Serie de potencias para niños
Una serie de potencias en matemáticas es como un polinomio muy, muy largo que nunca termina. Imagina que tienes una suma de términos donde cada término tiene una variable (como x) elevada a una potencia diferente (x⁰, x¹, x², x³, y así sucesivamente). Cada uno de estos términos está multiplicado por un número especial, llamado coeficiente.
La forma general de una serie de potencias es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_0 + a_1 (x-c)^1+ a_2 (x-c)^2 + a_3 (x-c)^3 + \ldots
Aquí, c es un número que llamamos el "centro" de la serie. Es el punto alrededor del cual la serie se organiza. Los números Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_0, a_1, a_2, \ldots son los coeficientes, que son simplemente valores fijos.
Las series de potencias son muy útiles en el análisis matemático. Por ejemplo, se usan para representar funciones complicadas de una manera más sencilla, como si fueran polinomios infinitos. Esto ayuda a entender mejor cómo se comportan esas funciones.
A veces, el centro c de la serie es cero. En ese caso, la serie se simplifica y se llama serie de Maclaurin: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots.
Además de su uso en el análisis matemático, las series de potencias también aparecen en otras áreas. Por ejemplo, en la Combinatoria, se usan como funciones generatrices para contar cosas de diferentes maneras. También son importantes en la ingeniería electrónica para analizar señales. Incluso la forma en que escribimos los números decimales (como 3.14159...) puede verse como un tipo de serie de potencias, donde la variable es 1/10.
Contenido
¿Cuándo funciona una serie de potencias? La convergencia
Una serie de potencias Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\textstyle \sum_{n=0}^\infty a_n(x-c)^n} no siempre funciona para cualquier valor de x. Decimos que una serie es "convergente" si, al sumar más y más términos, el resultado se acerca a un número específico. Si el resultado no se acerca a un número, decimos que es "divergente".
Siempre que x es igual a c (el centro de la serie), la serie converge. En este caso, el resultado es simplemente 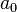 .
.
Para otros valores de x, la serie puede converger o divergir. Existe un número especial llamado el radio de convergencia, que se representa con la letra r.
- Si la distancia entre x y c es menor que r (es decir, |x – c| < r), la serie converge.
- Si la distancia entre x y c es mayor que r (es decir, |x – c| > r), la serie diverge.
El radio de convergencia puede ser cero (la serie solo converge en el centro), un número positivo, o incluso infinito (la serie converge para cualquier valor de x).
El conjunto de todos los valores de x para los que la serie converge se llama el disco de convergencia. Dentro de este disco, la serie se comporta muy bien: converge de forma "absoluta" y "uniforme", lo que significa que la suma se acerca al valor real de una manera muy ordenada.
Cuando la distancia entre x y c es exactamente igual a r (|x – c| = r), no podemos saber de inmediato si la serie converge o diverge. Depende de cada serie en particular.
¿Cómo se calcula el radio de convergencia?
Existen fórmulas para calcular el radio de convergencia. Una de las más comunes usa los coeficientes 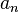 de la serie:
de la serie:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle r^{-1} = \lim_{n\to\infty}\left|{a_{n+1}\over a_n}\right|}
Esta fórmula funciona si el límite existe. Si no, hay otras fórmulas más complejas que se usan en matemáticas avanzadas.
Teorema de convergencia de series de potencias
Un teorema importante nos dice que si una función es "analítica" (lo que significa que se puede representar muy bien con una serie de potencias) en un área alrededor de un punto, entonces su serie de Taylor (un tipo especial de serie de potencias) converge en esa área y es igual a la función original.
En resumen, para cualquier serie de potencias, siempre hay un radio de convergencia único, R. Si un punto z está dentro de la distancia R del centro, la serie converge. Si está fuera de esa distancia, la serie diverge. Si está justo en el borde (a una distancia R), la convergencia puede variar.
Ejemplos de series de potencias
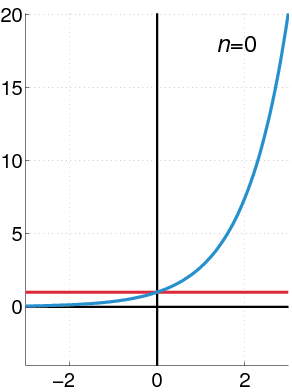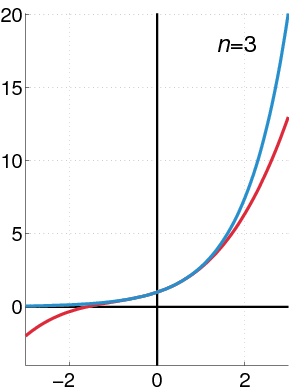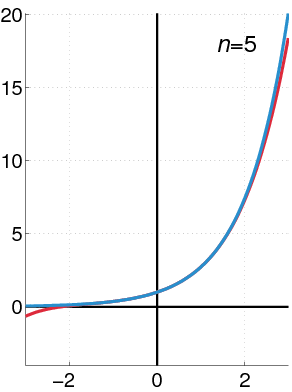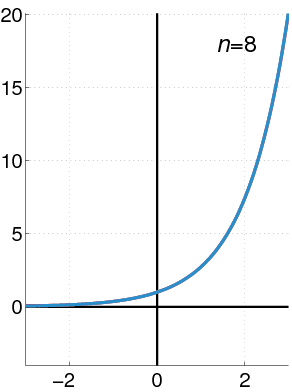
Aquí tienes algunos ejemplos famosos de series de potencias:
- La serie geométrica:
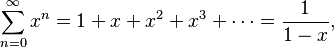 Esta serie converge si el valor absoluto de x es menor que 1 (es decir, |x|<1). Si |x| es mayor o igual a 1, la serie diverge. Es un ejemplo muy importante para entender cómo funcionan las series.
Esta serie converge si el valor absoluto de x es menor que 1 (es decir, |x|<1). Si |x| es mayor o igual a 1, la serie diverge. Es un ejemplo muy importante para entender cómo funcionan las series.
- La función exponencial (
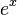 ):
):
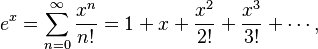 Esta serie es especial porque converge para cualquier valor de x (su radio de convergencia es infinito). Esto significa que puedes usar esta serie para calcular el valor de
Esta serie es especial porque converge para cualquier valor de x (su radio de convergencia es infinito). Esto significa que puedes usar esta serie para calcular el valor de 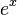 con mucha precisión.
con mucha precisión.
- La función seno (
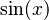 ):
):
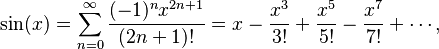 Al igual que la función exponencial, la serie del seno también converge para cualquier valor de x. Estas series son ejemplos de series de Taylor, que son una herramienta fundamental en matemáticas para aproximar funciones.
Al igual que la función exponencial, la serie del seno también converge para cualquier valor de x. Estas series son ejemplos de series de Taylor, que son una herramienta fundamental en matemáticas para aproximar funciones.
Véase también
 En inglés: Power series Facts for Kids
En inglés: Power series Facts for Kids
- Serie (matemáticas)
- Serie formal de potencias
- Serie de Laurent
- Convergencia
- Radio de convergencia
- Fórmula de Euler-Maclaurin
- Anexo:Series matemáticas

