Volumen para niños

Para otros usos de este término, véase Volumen (desambiguación).

Cuerpos geométricos o figuras geométricas «sólidas» que delimitan volúmenes

Jarra aforada para medir el volumen de líquidos

El volumen es una magnitud métrica de tipo escalar definida como la extensión en tres dimensiones de una región del espacio. Es una magnitud derivada de la longitud, ya que en un ortoedro se halla multiplicando tres longitudes: el largo, el ancho y la altura. Matemáticamente el volumen es definible no solo en cualquier espacio euclídeo, sino también en otro tipo de espacios métricos que incluyen por ejemplo a las variedades de Riemann.

Desde un punto de vista físico, los cuerpos materiales ocupan un volumen por el hecho de ser extensos, fenómeno que se debe al principio de exclusión de Pauli. La noción de volumen es más complicada que la de superficie y en su uso formal puede dar lugar a la llamada paradoja de Banach-Tarski.

La unidad de medida de volumen en el Sistema Internacional de Unidades es el metro cúbico. En el sistema métrico decimal, una unidad de volumen para sólidos era el estéreo, igual al metro cúbico, pero actualmente poco usada. En ese mismo sistema, para medir la capacidad de líquidos, se creó el litro, que es aceptado por el SI. Por razones históricas, existen unidades separadas para ambas, sin embargo están relacionadas por la equivalencia entre el litro y el decímetro cúbico:

1 dm³ = 1 litro = 0,001 m³ = 1000 cm³.

Unidades de volumen

Existen multitud de unidades de volumen escalar, que se utilizan dependiendo del contexto o de la finalidad de la medición. En los ámbitos académicos o técnicos se suelen emplear el metro y sus derivados. Para expresar el volumen de sustancias líquidas o gaseosas, e incluso para mercancías a granel, se suele recurrir a la capacidad del recipiente que lo contiene, medida en litros y sus derivados. En ocasiones, cuando la densidad del material es constante y conocida, se pueden expresar las cantidades por su equivalente en peso en lugar de en volumen.

Muchas de las unidades de volumen existentes se han empleado históricamente para el comercio de mercancías o para el uso diario. Aun compartiendo el mismo nombre, muchas unidades varían significativamente de una región a otra.

Sistema Internacional de Unidades

En el Sistema Internacional de Unidades la unidad de volumen es el metro cúbico.

Algunos de los múltiplos y submúltiplos usuales del metro cúbico son los siguientes:

Múltiplos	Submúltiplos
Kilómetro cúbico = 10⁹ m³ Hectómetro cúbico = 10⁶ m³ Decámetro cúbico = 10³ m³	Decímetro cúbico = 10⁻³ m³ Centímetro cúbico = 10⁻⁶ m³ Milímetro cúbico = 10⁻⁹ m³

La unidad más utilizada para medir el volumen de líquidos o recipientes es el litro. El litro está admitido en el S.I. aunque estrictamente no forma parte de él.

Sistema anglosajón de medidas

Las unidades de volumen en el sistema anglosajón de unidades se derivan de las respectivas unidades de longitud, como la pulgada cúbica, el pie cúbico, la yarda cúbica, el acre-pie o la milla cúbica. Para medir el volumen de líquidos, las unidades de capacidad más extendidas son el barril, el galón y la pinta, y en menor medida la onza líquida, el cuarto, el gill, el minim o el escrúpulo líquido.

Otras unidades de volumen

A lo largo de la historia, se han utilizado diferentes unidades de volumen que varían de una cultura a otra. En general, en casi todas ellas existían dos tipos de medida de volumen: para líquidos y para sólidos. Incluso el sistema métrico decimal original las definió como unidades diferentes: el litro (igual a 1 dm³) para líquidos y el estéreo (igual a 1 m³) para sólidos. Físicamente son equivalentes y actualmente no se establecen diferencias, pero antiguamente la medida, como concepto, estaba indisociablemente unida al método para llevarla a cabo (el diccionario académico recogíó hasta 1956 ‘lo que sirve para medir’ como una acepción de medida): así, el volumen se basaba en tomar las medidas longitudinales del cuerpo sólido y luego operar, mientras que la capacidad se basaba en lo que podían contener recipientes de determinados tamaños.

En la Antigua Grecia se utilizaban el dracma líquido o la metreta. En la antigua Roma se utilizaban medidas como el ánfora, el sextario o la hemina. En el antiguo Egipto la medida más utilizada era el heqat. En Castilla, se usaban unidades tradicionales como la arroba, la cántara, el celemín o la fanega, algunas de las cuales permanecen en uso hoy en día.

En el ámbito culinario, especialmente en los países anglosajones y los que están bajo su influencia, es habitual utilizar medidas de volumen dependientes de los distintos recipientes de uso frecuente, pero sin una definición precisa, como la cucharada, la cucharadita o la taza. Esta costumbre proviene de la falta de medidores de peso (balanzas) de suficiente precisión, tales como las que ahora existen.

En medicina y en enfermería, el volumen de una gota está definido con un diámetro estandarizado (1 mililitro son aproximadamente 20 gotas), pero no así en farmacia, pues, dependiendo del diámetro del dosificador de un medicamento, la equivalencia puede estar entre 15 y 40 gotas por mililitro.

Volumen de figuras simples

La siguiente tabla muestra la expresión matemática que relaciona el volumen con las dimensiones de figuras geométricas comunes:

Fórmulas comunes para el volumen
Figura	Fórmula	Variables
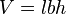Ortoedro	$V = l b h$	l = largo, b = ancho, h = altura
Cubo	$V = l^3$	l = longitud del lado
Cilindro 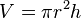(prisma circular)	$V = \pi r^2 h$	r = radio de la cara circular, h = distancia entre caras
Prisma de sección transversal constante en toda su altura	$V = A h$	A = área de la base, h = altura
Esfera	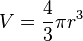$V = \frac{4}{3} \pi r^3$	r = radio de la esfera, que es la primera integral de la fórmula para el área superficial de una esfera
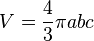Elipsoide	$V = \frac{4}{3} \pi abc$	a, b, c = semiejes del elipsoide
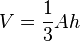Pirámide	$V = \frac{1}{3} A h$	A = área de la base, h = altura de la base al vértice superior
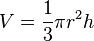Cono (pirámide de base circular)	$V = \frac{1}{3} \pi r^2 h$	r = radio del círculo de la base, h = distancia de la base al tope

El volumen de un paralelepípedo es el valor absoluto del triple producto escalar de los vectores correspondientes a tres aristas concurrentes, y es equivalente al valor absoluto del determinante de la matriz que forman los tres vectores.

Definición matemática

Espacios euclidianos

Matemáticamente, el volumen de una región del espacio euclídeo es la cantidad de espacio tridimensional obtenida por triple integración del elemento diferencial de volumen extendida a dicho dominio. Así el volumen de un cuerpo o región tridimensional $R \subset \R^3$ viene dado por:

$\mathrm{Vol}(R) = \int_R \mathrm{d}V = \int_R \mathrm{d}x\mathrm{d}y\mathrm{d}z = \int_{\R^3} \chi_R(x,y,z) \mathrm{d}x\mathrm{d}y\mathrm{d}z$

donde $\chi_R$ es la función característica de la región R:

$\chi_R(x,y,z) = \begin{cases} 1& (x,y,z)\in R\\ 0& (x,y,z)\notin R \end{cases}$

Dicha noción se puede generalizar a espacios de dimensiones superiores (véase hipervolumen).

Variedades riemannianas

En otras geometrías, se deben considerar los efectos locales de la métrica, expresados mediante el tensor métrico, sobre el elemento diferencial de volumen. Dada una subvariedad de Riemann (con clausura compacta) M de dimensión 3 su volumen, viene dado por la integración de la una 3-forma $\eta$ :

$\mathrm{Vol}(M) = \int_M \eta, \qquad \eta = \sqrt{g}\ \eta_{ijk} \mathrm{d}x^i \land \mathrm{d}x^j \land \mathrm{d}x^k$

donde g es precisamente el determinante del tensor métrico definido en toda la subvariedad riemanniana.

Generalizaciones

Dado un subconjunto compacto del espacio euclídeo tridimensional o de una variedad riemanniana de dimensión 3 puede definirse el volumen de dicho subconjunto mediante la medida de Hausdorff-Besicovitch para definir el volumen dicho subconjunto. El número calculado así será un número del intervalo $\scriptstyle [0,\infty)$ .

Véase también

En inglés: Volume Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Volumen&oldid=3900068»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Volumen para Niños. Enciclopedia Kiddle.