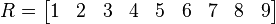Matriz (matemática) para niños
En matemática, una matriz es como una tabla de números organizada en filas y columnas. Imagina una cuadrícula donde cada casilla tiene un número. Las matrices se usan para organizar información y resolver problemas en muchas áreas, desde la computación hasta la ingeniería.
Una matriz se nombra con una letra mayúscula, como la letra A. Los números dentro de la matriz se llaman elementos y se escriben con la misma letra en minúscula, pero con dos números pequeños (subíndices). El primer subíndice te dice en qué fila está el número, y el segundo te dice en qué columna. Por ejemplo, a12 sería el número que está en la primera fila y la segunda columna.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix}_{ m\times n}
Si una matriz tiene m filas y n columnas, decimos que es una matriz de tamaño m por n (se escribe mxn). Las matrices se pueden sumar, multiplicar y usar de muchas maneras, lo que las hace muy importantes en una parte de las matemáticas llamada álgebra lineal.
Contenido
Historia de las matrices
Las matrices no son un invento nuevo; su historia es muy antigua.
| Año | Acontecimiento |
|---|---|
| 200 a.C. | Matemáticos en China usan arreglos de números. |
| 1848 | James Joseph Sylvester usa por primera vez la palabra «matriz». |
| 1858 | Arthur Cayley publica un trabajo importante sobre matrices. |
| 1878 | Ferdinand Georg Frobenius descubre resultados importantes sobre matrices. |
| 1925 | Werner Heisenberg usa matrices en la mecánica cuántica. |
Desde hace mucho tiempo se estudiaron los "cuadrados mágicos", que son arreglos de números donde la suma de cada fila, columna y diagonal es la misma. Un cuadrado mágico de 3x3 se menciona en textos chinos alrededor del año 650 a.C.
El uso de matrices para resolver ecuaciones lineales también tiene una larga historia. Un texto matemático chino llamado Nueve capítulos sobre el Arte de las matemáticas, de entre el 300 a.C. y el 200 a.C., es el primer ejemplo conocido de cómo se usaron las matrices para resolver sistemas de ecuaciones.
Matemáticos como Seki Kōwa en Japón (1683) y Gottfried Leibniz en Alemania (1693) también trabajaron con ideas relacionadas con las matrices. Más tarde, en el siglo XVIII, Gabriel Cramer presentó la regla de Cramer para resolver ecuaciones. En el siglo XIX, Carl Friedrich Gauss y Wilhelm Jordan desarrollaron la eliminación de Gauss-Jordan, un método muy útil para trabajar con matrices.
Fue James Joseph Sylvester quien, entre 1848 y 1850, usó por primera vez la palabra "matriz". En 1858, Arthur Cayley introdujo la notación matricial, que es una forma más corta de escribir sistemas de ecuaciones.
Muchos matemáticos famosos, como Cayley, William Rowan Hamilton, Hermann Grassmann, Ferdinand Georg Frobenius, Olga Taussky-Todd y John von Neumann, contribuyeron al estudio de las matrices. En 1925, Werner Heisenberg redescubrió el cálculo con matrices y lo usó para crear una parte de la mecánica cuántica, una rama de la física.
Durante la II Guerra Mundial, Olga Taussky-Todd usó la teoría de matrices para investigar un problema de inestabilidad en aviones.
¿Qué es una matriz?
Una matriz es un conjunto de números organizados en filas (horizontales) y columnas (verticales). Si una matriz tiene m filas y n columnas, se le llama "matriz m por n" (se escribe mxn).
Dos matrices son iguales si tienen el mismo tamaño y los mismos números en las mismas posiciones. El número que está en la fila i y la columna j se llama elemento i,j o elemento (i,j).
Las matrices se escriben con letras mayúsculas (como A), y sus elementos con la misma letra en minúscula y subíndices (como aij). Si los subíndices tienen dos cifras, se usa una coma para separarlos, por ejemplo, a23,100.
A veces, para que sea más fácil distinguirlas, las matrices se escriben con letras en negrita, como A.
Tipos especiales de matrices
- Un vector fila es una matriz que tiene solo una fila (1xn).
- Un vector columna es una matriz que tiene solo una columna (mx1).
- Las matrices cuadradas son aquellas que tienen el mismo número de filas que de columnas (nxn).
Ejemplo de matriz
Aquí tienes un ejemplo de una matriz A de tamaño 4x3:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 7 \\ 4 & 9 & 2 \\ 6 & 0 & 5 \\ \end{pmatrix}
En esta matriz, el elemento a23 (fila 2, columna 3) es el número 7.
Y aquí un ejemplo de un vector fila R de tamaño 1x9:
Operaciones básicas con matrices
Podemos hacer varias operaciones con matrices, que son muy útiles en diferentes campos.
Suma de matrices
Para sumar dos matrices, deben tener el mismo tamaño (el mismo número de filas y columnas). La suma se hace elemento por elemento. Es decir, sumas el número de la posición (1,1) de la primera matriz con el número de la posición (1,1) de la segunda, y así sucesivamente.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{pmatrix} 2 & 2 & 1 \\ 3 & 2 & 1 \\ 2 & 3 & 2 \\ 2 & 0 & 4 \end{pmatrix} \quad + \quad \begin{pmatrix} 0 & 1 & 4 \\ 1 & 4 & 0 \\ 2 & 1 & 1 \\ 0 & 2 & 2 \end{pmatrix} \quad = \quad \begin{pmatrix} 2 & 3 & 5 \\ 4 & 6 & 1 \\ 4 & 4 & 3 \\ 2 & 2 & 6 \end{pmatrix}
Aquí tienes otro ejemplo:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{pmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 0 & 5 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \end{pmatrix} = \begin{pmatrix} 1+1 & 3+0 & 2+5 \\ 1+7 & 0+5 & 0+0 \\ 1+2 & 2+1 & 2+1 \end{pmatrix} = \begin{pmatrix} 2 & 3 & 7 \\ 8 & 5 & 0 \\ 3 & 3 & 3 \end{pmatrix}
La suma de matrices tiene propiedades similares a la suma de números:
- Asociatividad: Puedes agrupar las matrices de diferentes maneras al sumar: (A+B)+C = A+(B+C).
- Conmutatividad: El orden de la suma no importa: A+B = B+A.
- Elemento neutro: Existe una matriz de ceros (matriz nula) que, al sumarla, no cambia la matriz original: A+0 = A.
- Inverso aditivo: Para cada matriz A, existe una matriz -A (con todos sus elementos cambiados de signo) que, al sumarla, da la matriz nula: A+(-A) = 0.
Producto por un número (escalar)
Multiplicar una matriz por un número (llamado "escalar") significa multiplicar cada elemento de la matriz por ese número. El resultado es una matriz del mismo tamaño.
Por ejemplo, si multiplicamos la matriz A por el número 2:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 \begin{pmatrix} 1 & \,\,\ \, 8 & -3 \\ 4 & -2 & \,\,\, 6 \end{pmatrix} = \begin{pmatrix} 2(1) & \,\,\,\,2(8) & 2(-3) \\ 2(4) & 2(-2) & \,\,\,\,2(6) \end{pmatrix} = \begin{pmatrix} 2 & \, 16 & -6 \\ 8 & -4 & \,12 \end{pmatrix}
Esta operación también tiene propiedades importantes:
- Asociatividad: Puedes agrupar los números al multiplicar: (λμ)A = λ(μA).
- Distributividad: El número se distribuye sobre la suma de matrices: λ(A+B) = λA + λB.
- Distributividad sobre la suma de números: (λ+μ)A = λA + μA.
- Producto por el número 1: Multiplicar por 1 no cambia la matriz: 1A = A.
Producto de matrices
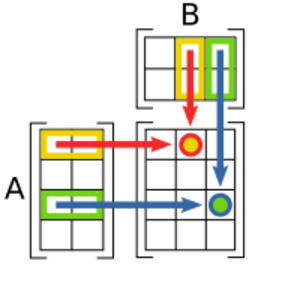
El producto de matrices es un poco más complejo. No se multiplican elemento por elemento como en la suma. Para poder multiplicar dos matrices, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda.
Si tienes una matriz A de tamaño nxm y una matriz B de tamaño mxp, el resultado será una matriz C de tamaño nxp. Cada elemento cij de la matriz resultante se calcula multiplicando los elementos de la fila i de la primera matriz por los elementos de la columna j de la segunda matriz y sumando esos productos.
Por ejemplo:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{pmatrix} \,\,\ \, 1 & 0 & 2 \\ -1 & 3 & 1 \end{pmatrix} \begin{pmatrix} 3 & 1 \\ 2 & 1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} \, \,\,\, 1(3)+0(2)+2(1) & \,\,\,\,1(1)+0(1)+2(0) \\ -1(3)+3(2)+1(1) & -1(1)+3(1)+1(0) \\ \end{pmatrix} = \begin{pmatrix} 5 & 1 \\ 4 & 2 \\ \end{pmatrix}
El producto de matrices tiene estas propiedades:
- Asociatividad: A(BC) = (AB)C.
- Distributividad por la derecha: (A+B)C = AC + BC.
- Distributividad por la izquierda: A(B+C) = AB + AC.
Es muy importante saber que el producto de matrices no es conmutativo. Esto significa que, en general, A por B (AB) no es lo mismo que B por A (BA). Incluso puede que AB se pueda calcular, pero BA no, si los tamaños no coinciden.
Otros conceptos importantes
Matriz traspuesta
La traspuesta de una matriz se obtiene cambiando sus filas por sus columnas. Si la matriz original es de nxm, su traspuesta será de mxn. Se denota con un superíndice T, como AT.
Ejemplo: Si la matriz A es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{pmatrix} 1 & \,\,\ \,8 & -3 \\ 4 & -2 & \,\,\ 6 \end{pmatrix}_{2\times 3}
Su traspuesta es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{pmatrix} 1 & 4 \\ 8 & -2 \\ -3 & 6 \end{pmatrix}_{3\times 2 }
Las propiedades de la traspuesta son:
- (AT)T = A
- (A+B)T = AT + BT
- (AB)T = BTAT
Matrices cuadradas y conceptos relacionados
Una matriz cuadrada tiene el mismo número de filas que de columnas. Son muy importantes en matemáticas.
La matriz identidad In es una matriz cuadrada especial. Tiene números 1 en su diagonal principal (desde la esquina superior izquierda hasta la inferior derecha) y ceros en todas las demás posiciones. Es como el número 1 en la multiplicación: si multiplicas cualquier matriz por la matriz identidad, el resultado es la misma matriz.
Por ejemplo, la matriz identidad de orden 3 (I3) es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf{I}_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}
Una matriz cuadrada A es invertible (o regular) si existe otra matriz B que, al multiplicarlas, da como resultado la matriz identidad (AB = I). A esta matriz B se le llama la matriz inversa de A, y se escribe A-1.
El determinante de una matriz cuadrada es un número especial que se calcula a partir de sus elementos. Si el determinante de una matriz es diferente de cero, entonces la matriz es invertible.
La traza de una matriz cuadrada es la suma de los números que están en su diagonal principal.
Aplicaciones de las matrices
Las matrices en la computación
Las matrices son muy usadas en la computación porque son una forma eficiente de organizar y manejar grandes cantidades de información.
- Se usan para representar grafos (diagramas con puntos y líneas que muestran conexiones).
- Son fundamentales en el cálculo numérico, que es la parte de las matemáticas que resuelve problemas usando aproximaciones.
- En la computación gráfica, las matrices son clave para crear animaciones de objetos y formas en videojuegos y películas.
Ejemplo de brazo robótico
Las matrices también se aplican en la robótica. Por ejemplo, para programar un brazo robótico como el Lynx6, se usan matrices. Este brazo tiene 5 ejes que le permiten moverse de forma rápida y precisa.
Para programar sus movimientos, se usan dos modelos principales:
- El modelo FK (cinemática directa) usa matrices para calcular la posición y orientación del extremo del brazo (la "mano") a partir de los ángulos de sus articulaciones.
- El modelo IK (cinemática inversa) hace lo contrario: calcula los ángulos de las articulaciones necesarios para que el extremo del brazo llegue a una posición y orientación deseadas.
Las matrices de transformación ayudan a relacionar cómo se mueve cada parte del brazo robótico. Multiplicando estas matrices, se puede saber la posición final del brazo.
Matrices en teoría de grafos
En la teoría de los grafos, las matrices se usan para representar las conexiones entre los puntos (vértices) de un grafo.
- La matriz de adyacencia es una matriz que muestra si hay una conexión directa entre dos vértices. Si hay una conexión, se pone un 1; si no, un 0.
- La matriz de incidencia es otro tipo que muestra qué vértices están conectados a qué líneas (aristas).
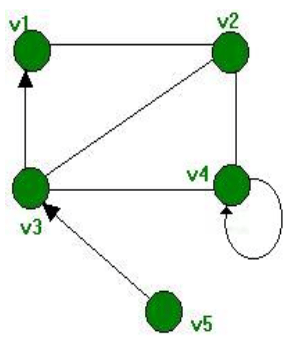
Aquí tienes un ejemplo de un grafo y su matriz de adyacencia:
| / | V1 | V2 | V3 | V4 | V5 |
|---|---|---|---|---|---|
| V1 | 0 | 1 | 0 | 0 | 0 |
| V2 | 1 | 0 | 1 | 1 | 0 |
| V3 | 1 | 1 | 0 | 1 | 0 |
| V4 | 0 | 1 | 1 | 1 | 0 |
| V5 | 0 | 0 | 1 | 0 | 0 |
En esta matriz, un 1 significa que hay una conexión entre los vértices, y un 0 significa que no la hay. Por ejemplo, V1 está conectado a V2 (hay un 1 en V1/V2), pero no a V3 (hay un 0 en V1/V3).
A veces, la conexión tiene un sentido. Por ejemplo, en la posición V3/V5 hay un 0, pero en V5/V3 hay un 1. Esto significa que se puede ir de V5 a V3, pero no de V3 a V5.
Otros usos de las matrices
- Las matrices son una parte fundamental del álgebra lineal, que es una rama de las matemáticas que estudia vectores, espacios vectoriales y transformaciones lineales.
- Las matrices estocásticas se usan en probabilidad y estadística para estudiar procesos que cambian con el tiempo de forma aleatoria.
- Las matrices definidas positivas se usan para encontrar los puntos más altos o más bajos de funciones en matemáticas.
- En teoría de control, se usan matrices con elementos que son polinomios para diseñar sistemas de control.
Teoremas importantes
- Teorema de Cayley-Hamilton
- Teorema de Gerschgorin
Véase también
 En inglés: Matrix (mathematics) Facts for Kids
En inglés: Matrix (mathematics) Facts for Kids
- Cálculo matricial
- Determinante (matemática)
- Eliminación de Gauss-Jordan
- Matlab