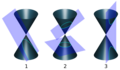Sección cónica para niños
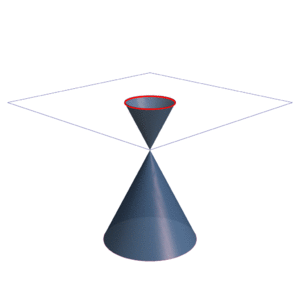
En matemáticas, especialmente en geometría, las secciones cónicas son curvas especiales que se forman cuando cortamos un cono con un plano. Imagina un cono de helado muy largo, que se extiende hacia arriba y hacia abajo (un "cono doble"). Si lo cortas con una superficie plana de diferentes maneras, obtendrás estas curvas.
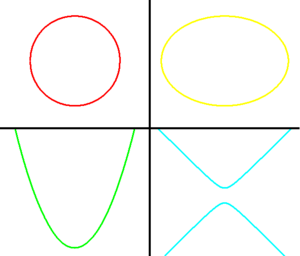
Las secciones cónicas más conocidas son la elipse, la parábola, la hipérbola y la circunferencia. Cada una tiene una forma única y propiedades interesantes.
Una forma de entender estas curvas es pensando en un punto especial llamado foco y una línea especial llamada directriz. Para una cónica (que no sea un círculo), todos sus puntos tienen una relación fija entre su distancia al foco y su distancia a la directriz. Esta relación se llama excentricidad y nos dice qué tipo de cónica es.
También podemos describir estas curvas con ecuaciones matemáticas. En geometría analítica, una cónica es una curva que se puede representar con una ecuación de segundo grado, como por ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Ax^2 + Bxy + Cy^2 +Dx + Ey + F = 0.
Contenido
¿De dónde vienen los nombres de las cónicas?
La idea de las secciones cónicas es muy antigua. La primera vez que se definieron fue en la Antigua Grecia, alrededor del año 340 a. C., por un matemático llamado Menecmo. Él las describió como cortes de un cono.
Los nombres que usamos hoy, como hipérbola, parábola y elipse, fueron dados por otro matemático griego, Apolonio de Perge.
Hoy en día, podemos definir las secciones cónicas de varias maneras, usando diferentes ramas de las matemáticas.
¿Cómo se forman las secciones cónicas?
Las secciones cónicas se han estudiado por miles de años. Son muy importantes en la geometría euclidiana, que es la geometría que aprendemos en la escuela.
Definición de las cónicas
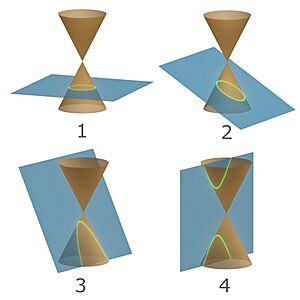
Una cónica es la curva que se forma cuando un plano (una superficie plana) corta la superficie de un cono doble. Un cono doble es como dos conos unidos por sus puntas.
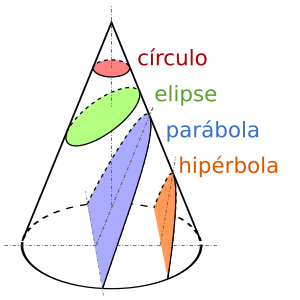
Hay tres tipos principales de cónicas: la elipse, la parábola y la hipérbola. El círculo es un tipo especial de elipse.
- La circunferencia se forma cuando el plano corta el cono de forma completamente horizontal, es decir, perpendicular al eje del cono.
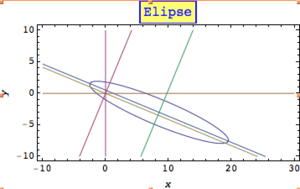
- La elipse se forma cuando el plano corta el cono de forma inclinada, pero sin ser paralelo a ninguna de las líneas que forman el cono. La elipse es una curva cerrada.
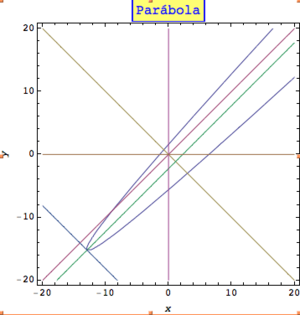
- La parábola se forma cuando el plano corta el cono de forma paralela a una de las líneas que forman el cono. La parábola es una curva abierta.
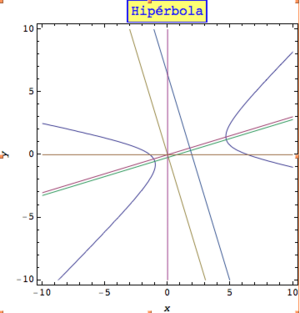
- La hipérbola se forma cuando el plano corta ambas partes del cono doble. Esto crea dos curvas separadas y abiertas.
Si el plano pasa justo por la punta (vértice) del cono, se forman casos especiales llamados "cónicas degeneradas". Estas pueden ser un solo punto, una línea o dos líneas que se cruzan.
Excentricidad, foco y directriz
.
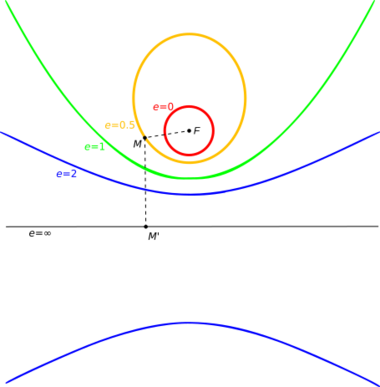
Podemos definir una sección cónica de otra manera, usando solo geometría plana. Una cónica es el conjunto de todos los puntos que cumplen una condición especial: la distancia de cada punto a un punto fijo (el foco) es un número constante (la excentricidad, que se representa con la letra e) multiplicado por la distancia de ese mismo punto a una línea fija (la directriz).
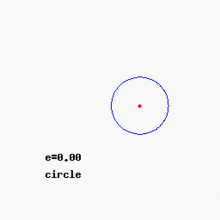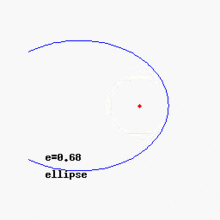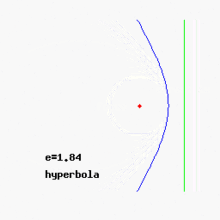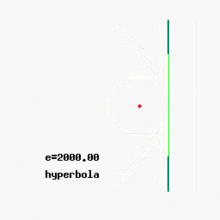
- Si la excentricidad e está entre 0 y 1 (0 < e < 1), obtenemos una elipse.
- Si la excentricidad e es igual a 1 (e = 1), obtenemos una parábola.
- Si la excentricidad e es mayor que 1 (e > 1), obtenemos una hipérbola.
Un círculo es un caso especial donde la excentricidad es cero (e = 0). Su foco es el centro del círculo.
La excentricidad de una elipse nos dice qué tan "aplastada" es. Si la excentricidad es cercana a cero, la elipse es casi un círculo. Si es cercana a 1, es más alargada.
Tipos de secciones cónicas y sus ángulos
La forma de la sección cónica depende del ángulo con el que el plano corta el cono. Imagina que el ángulo del cono es α y el ángulo de inclinación del plano respecto al eje del cono es β.
- Si β es menor que α (β < α): Se forma una hipérbola.
- Si β es igual a α (β = α): Se forma una parábola.
- Si β es mayor que α (β > α): Se forma una elipse.
- Si β es igual a 90° (el plano es horizontal): Se forma una circunferencia (que es un tipo especial de elipse).
Ecuación general de segundo grado
Las secciones cónicas también se pueden describir con una ecuación matemática general. Esta ecuación es de segundo grado y tiene dos variables, x e y.
La forma general de esta ecuación es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0
Los valores de las letras a, h, b, g, f y c nos dicen qué tipo de cónica es. Por ejemplo:
- Si a es igual a b y h es igual a 0, la ecuación representa una circunferencia.
Estas ecuaciones nos permiten dibujar las cónicas en un plano de coordenadas.
Características de cada cónica
La Elipse
La elipse es una curva donde la suma de las distancias desde cualquier punto de la curva a dos puntos fijos (llamados focos) es siempre la misma.
Elementos importantes de una elipse:
- Centro: El punto medio de la elipse.
- Eje mayor: La línea más larga que pasa por el centro y los focos.
- Eje menor: La línea más corta que pasa por el centro, perpendicular al eje mayor.
- Distancia focal: La distancia desde el centro a uno de los focos.
La Hipérbola
La hipérbola es una curva donde la diferencia de las distancias desde cualquier punto de la curva a dos puntos fijos (también llamados focos) es siempre la misma.
Las hipérbolas tienen dos ramas separadas y dos líneas llamadas asíntotas. Las asíntotas son líneas a las que la curva se acerca cada vez más, pero nunca las toca, a medida que se extiende hacia el infinito.
Elementos importantes de una hipérbola:
- Centro: El punto medio entre los dos focos.
- Vértices: Los puntos de la curva más cercanos al centro.
- Distancia entre los vértices.
- Distancia entre los focos.
La Parábola
La parábola es una curva donde cada punto está a la misma distancia de un punto fijo (el foco) y de una línea fija (la directriz).
Elementos importantes de una parábola:
- Foco: El punto fijo.
- Directriz: La línea fija.
- Eje: Una línea que pasa por el foco y es perpendicular a la directriz. La parábola es simétrica respecto a este eje.
- Vértice: El punto de la parábola que está en el eje.
Aplicaciones de las cónicas
Las curvas cónicas son muy importantes en muchas áreas:
- Astronomía: Las trayectorias de los planetas alrededor del Sol son elipses. Los cometas pueden seguir trayectorias elípticas, parabólicas o hiperbólicas.
- Aerodinámica e industria: Se usan para diseñar formas perfectas en aviones, coches y otras máquinas, porque se pueden repetir con mucha precisión.
- Antenas: Las antenas parabólicas, por ejemplo, usan la forma de una parábola para concentrar las señales en un solo punto (el foco).
Historia de las secciones cónicas
Menecmo y los primeros estudios
Se cree que el matemático griego Menecmo (alrededor del 340 a. C.) fue el primero en definir las secciones cónicas. Él las usó para resolver un problema matemático antiguo. En ese tiempo, los conos se hacían girando un triángulo rectángulo. Las cónicas se obtenían cortando estos conos con un plano perpendicular a una de sus líneas. El tipo de cónica dependía del ángulo del cono.
Otros matemáticos griegos como Euclides y Arquímedes también estudiaron las cónicas. Arquímedes, por ejemplo, calculó el área de una parábola.
Apolonio de Perga
El matemático griego Apolonio de Perga (alrededor del 190 a. C.) hizo el mayor avance en el estudio de las cónicas. Sus ocho libros sobre "Secciones Cónicas" resumieron y ampliaron todo el conocimiento de la época. Él demostró que cualquier plano que corte un cono doble, sin importar el ángulo, producirá una de las cónicas que conocemos hoy. Apolonio fue quien les dio los nombres de "elipse", "parábola" e "hipérbola".
Más tarde, Papo de Alejandría (alrededor del 350 d. C.) destacó la importancia del concepto de foco y directriz para las cónicas.
Contribuciones en el mundo islámico
Las obras de Apolonio fueron traducidas al árabe. Matemáticos como Abū Sahl al-Qūhī (alrededor del año 1000) describieron instrumentos para dibujar cónicas. El famoso matemático y poeta persa Omar Jayam usó las cónicas para resolver ecuaciones matemáticas complejas.
Desarrollo en Europa
En Europa, Johannes Kepler (siglo XVII) usó el término "focos" y amplió la teoría de las cónicas.
Matemáticos como Girard Desargues y Blaise Pascal desarrollaron una nueva forma de geometría para estudiar las cónicas. René Descartes y Pierre Fermat aplicaron la geometría analítica, lo que permitió describir las cónicas con ecuaciones algebraicas.
John Wallis fue el primero en definir las secciones cónicas como soluciones de ecuaciones de segundo grado en 1655. Jan de Witt también escribió un libro importante sobre el tema y fue quien inventó la palabra "directriz".
Véase también
 En inglés: Conic section Facts for Kids
En inglés: Conic section Facts for Kids
- Circunferencia
- Elipse
- Parábola
- Hipérbola
- Esferas de Dandelin
Galería de imágenes