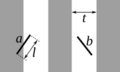Número π para niños
El número π (se pronuncia "pi") es una constante matemática muy importante. Representa la relación entre la longitud de una circunferencia (el borde de un círculo) y su diámetro (la línea que cruza el círculo por el centro). No importa el tamaño del círculo, esta relación siempre es la misma.
π es un número irracional, lo que significa que no se puede escribir como una fracción simple (como 1/2 o 3/4). Sus decimales se extienden infinitamente sin repetirse en un patrón.
El valor de π, con sus primeras cifras, es: 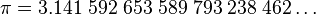 (sucesión A000796 en OEIS)
(sucesión A000796 en OEIS)
Este número se usa mucho en matemáticas, física e ingeniería para calcular cosas relacionadas con círculos, esferas y otros objetos redondos.
Datos para niños Lista de números – Números irracionalesζ(3) – √2 – √3 – √5 – φ – α – e – π – δ |
|
| Binario | 11.00100100001111110110… |
| Decimal | 3.14159265358979323846… |
| Hexadecimal | 3.243F6A8885A308D31319… |
| Fracción continua | 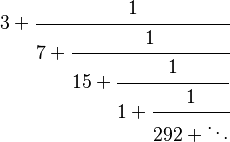 Nótese que la fracción continua no es periódica. |
Contenido
¿De dónde viene el nombre "Pi"?
La letra griega π se usa para representar este número. Viene de las palabras griegas "περιφέρεια" (periferia) y "περίμετρον" (perímetro), que se refieren al contorno de un círculo.
El matemático galés William Jones propuso usar este símbolo en 1706. Sin embargo, fue el famoso matemático Leonhard Euler quien lo hizo popular en 1748 con su libro Introducción al cálculo infinitesimal. Antes, a π se le conocía como "constante de Ludolph" o "constante de Arquímedes".
Características de Pi
¿Qué es Pi exactamente?
El matemático griego Euclides fue el primero en demostrar que la relación entre la circunferencia de un círculo y su diámetro es siempre la misma.
La definición más común de π es:
- π es la relación entre la longitud de cualquier circunferencia y su diámetro.
También podemos pensar en π como:
- El área de un círculo que tiene un radio de 1 unidad.
¿Por qué Pi es un número especial?
Pi es un número irracional, lo que significa que no se puede escribir como una fracción de dos números enteros. Esto fue demostrado por Johann Heinrich Lambert en 1761.
Además, π es un número trascendente. Esto quiere decir que no es la solución de ninguna ecuación de polinomio con números enteros. El matemático alemán Ferdinand Lindemann demostró esto en el siglo XIX. Esta demostración también resolvió un antiguo problema matemático llamado la "cuadratura del círculo", mostrando que es imposible resolverlo usando solo regla y compás.
Primeros decimales de Pi
Aunque π tiene infinitos decimales, aquí te mostramos los primeros cincuenta: 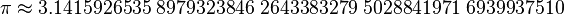 En la ciencia y la ingeniería, normalmente no se necesitan tantos decimales. Con unos pocos, ya se obtiene una precisión increíble. Por ejemplo, con cuarenta decimales de π se podría describir la curvatura de nuestra galaxia, la Vía Láctea, con un error más pequeño que el tamaño de un protón.
En la ciencia y la ingeniería, normalmente no se necesitan tantos decimales. Con unos pocos, ya se obtiene una precisión increíble. Por ejemplo, con cuarenta decimales de π se podría describir la curvatura de nuestra galaxia, la Vía Láctea, con un error más pequeño que el tamaño de un protón.
Historia del cálculo de Pi
A lo largo de la historia, muchas civilizaciones y matemáticos han intentado calcular el valor de π con la mayor precisión posible.
Antiguas civilizaciones
- Mesopotamia (1900-1600 a. C.): Algunos matemáticos de Mesopotamia usaban el valor de 3 para π, y en ocasiones, una aproximación más cercana como 3 + 1/7 (aproximadamente 3.142857).
- Antiguo Egipto (1800 a. C.): El Papiro de Ahmes menciona una forma de calcular el área de un círculo que implica un valor de π de aproximadamente 3.16049.
- La Biblia (950 a. C.): En algunos versículos de la Biblia, se describe un "Mar de metal fundido" con un diámetro de 10 codos y un contorno de 30 codos, lo que sugiere un valor de 3 para π. Sin embargo, esto podría ser un redondeo de las medidas.
Antigüedad clásica

- Arquímedes (siglo III a. C.): Este matemático griego fue muy ingenioso. Calculó π inscribiendo y circunscribiendo polígonos regulares (con muchos lados) dentro y fuera de un círculo. Empezó con hexágonos y fue doblando el número de lados hasta llegar a polígonos de 96 lados. Con esto, determinó que π estaba entre 3 10/71 y 3 1/7, lo que es una aproximación muy buena.
- Claudio Ptolomeo (siglo II d. C.): Este astrónomo y matemático griego dio una aproximación fraccionaria de 377/120, que es aproximadamente 3.1416.
Matemáticos de Asia
- China (siglos II-V d. C.):
* Zhang Heng (120 d. C.) usó la aproximación de la raíz cuadrada de 10 (aproximadamente 3.1623). * Liu Hui (263 d. C.) sugirió que 3.14 era una buena aproximación y luego calculó 3.14159 usando polígonos de muchos lados. * Zu Chongzhi (finales del siglo V) calculó π con una precisión de 3.1415926 y 3.1415927. También dio las fracciones 22/7 y 355/113, siendo esta última muy precisa y no superada por siglos.
- India (siglos V-XV d. C.):
* Aryabhata (finales del siglo V) estimó π en 3.1416. * Madhava (hacia 1400) obtuvo una aproximación exacta hasta 11 dígitos (3.14159265359) usando series matemáticas, siendo el primero en hacerlo.
- Mundo Islámico (siglo IX-XV d. C.):
* Al-Jwarizmi (siglo IX) mencionó que la gente común usaba 22/7, los geómetras 3, y los astrónomos 3.1416. * Ghiyath al-Kashi (siglo XV) calculó π con una precisión de 16 dígitos decimales.
Época moderna (antes de las computadoras)

- Ludolph van Ceulen (1610): Calculó los primeros 35 decimales de π. Se dice que estaba tan orgulloso que lo mandó grabar en su lápida.
- Isaac Newton (1665): Desarrolló una serie matemática para calcular π.
- John Wallis (1655)** y **Leibniz (1682): También crearon series matemáticas para aproximar π.
- William Jones (1706): Fue quien propuso usar la letra griega π como símbolo.
- William Shanks (1873): Dedicó 20 años a calcular los decimales de π a mano, obteniendo 707. Sin embargo, en 1944 se descubrió un error en el decimal 528, lo que hizo que los siguientes fueran incorrectos.
Época de las computadoras
Con la llegada de las computadoras, el cálculo de π dio un salto gigantesco.
- 1949: La primera computadora, la ENIAC, calculó 2037 decimales en 70 horas.
- Década de 1960: Las computadoras IBM batieron récords, llegando a 250,000 decimales en 1966.
- Siglo XXI: Las supercomputadoras han alcanzado cifras asombrosas. En 2009, el sistema T2K Tsukuba calculó más de 2.5 billones de decimales.
- Récords recientes: En 2021, un equipo de la Universidad de Ciencias Aplicadas de los Grisones calculó más de 62 billones de decimales. ¡Y en 2025, se espera alcanzar los 300 billones!
Estos cálculos no solo demuestran la potencia de las computadoras, sino que también son una forma de probar su funcionamiento y capacidad.
Usos de Pi en la ciencia
Pi aparece en muchas áreas de las matemáticas y la ciencia, incluso donde no hay círculos directamente.
Geometría y Trigonometría
- Para cualquier círculo de radio r, la longitud de su circunferencia es 2πr y su área es πr².
- Pi también aparece en las fórmulas para el área y volumen de otras figuras redondas como elipses, esferas, conos y toroides.
- En trigonometría, las funciones como el seno y el coseno se repiten cada 2π. Esto significa que un giro completo de 360 grados es igual a 2π radianes.
Física
Pi es fundamental en ecuaciones que describen principios básicos del universo, especialmente en fenómenos que se repiten, como las ondas y los ciclos.
- Aparece en el Principio de incertidumbre de Heisenberg de la mecánica cuántica, que describe los límites de lo que podemos saber sobre partículas muy pequeñas.
- También está en la Ecuación del campo de Einstein de la relatividad general, que explica cómo funciona la gravedad.
- En la Ley de Coulomb, que describe la fuerza entre cargas eléctricas.
- Y en la Tercera ley de Kepler, que explica el movimiento de los planetas alrededor del Sol.
Probabilidad y Estadística
Pi también se encuentra en fórmulas de probabilidad y estadística.
- La distribución normal, que es muy común para describir datos que se agrupan alrededor de un promedio (como las alturas de las personas), usa π en su fórmula.
- El famoso problema de la "aguja de Buffon" es un experimento donde se lanza una aguja sobre un papel con líneas paralelas. La probabilidad de que la aguja cruce una línea se puede aproximar usando π.
Fórmulas importantes con Pi
En Geometría
- Longitud de la circunferencia de radio r: C = 2 π r
- Área del círculo de radio r: A = π r²
- Volumen de la esfera de radio r: V = (4/3) π r³
- Volumen de un cilindro de radio r y altura h: V = π r² h
En Análisis Matemático
- Serie de Leibniz: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots = \frac{\pi}{4}
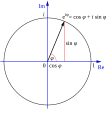
- Identidad de Euler:
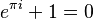 (Esta es una de las fórmulas más bellas de las matemáticas, ya que conecta cinco constantes fundamentales: e, i, π, 1 y 0).
(Esta es una de las fórmulas más bellas de las matemáticas, ya que conecta cinco constantes fundamentales: e, i, π, 1 y 0). - Problema de Basilea (resuelto por Euler): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots = \frac{\pi^2}{6}
Pi en la cultura popular
Reglas mnemotécnicas
Para recordar los primeros dígitos de π, la gente usa poemas donde el número de letras de cada palabra corresponde a un dígito de π.
- Para 20 dígitos: "Soy y seré a todos definible, mi nombre tengo que daros, cociente diametral siempre inmedible, soy de los redondos aros." (Contando las letras: 3.14159265358979323846)
- En inglés, para 14 dígitos: "How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!" (3.14159265358979)
Existen historias y cuentos mucho más largos que permiten memorizar cientos o miles de dígitos de π.
Días de Pi
Hay días especiales para celebrar π:
- 14 de marzo: Es el "Día de Pi" (3/14 en el formato de fecha de Estados Unidos). Coincidentemente, es el cumpleaños de Albert Einstein y el aniversario del fallecimiento de Stephen Hawking.
- 22 de julio: Se celebra porque 22/7 es una aproximación común de π.
Pi en películas y series
- La película Pi (1998) trata sobre un matemático obsesionado con encontrar patrones numéricos en el mundo.
- En la serie The Simpsons, el profesor Frink bromea diciendo que "¡π es tres exactamente!" para llamar la atención.
- En la novela Contacto de Carl Sagan, π es un número que esconde un mensaje sobre la esencia del universo.
Curiosidades de Pi
- El método de Arquímedes para calcular π no fue superado en casi dos mil años.
- Hay programas en internet que pueden buscar tu número de teléfono en los primeros millones de dígitos de π.
- El japonés Akira Haraguchi rompió el récord mundial en 2006 recitando 100,000 dígitos de π de memoria.
- La probabilidad de que dos números enteros positivos elegidos al azar no tengan factores comunes (sean "primos entre sí") es
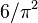 .
.
Galería de imágenes
-
Detalle del papiro Rhind
-
Método de aproximación de Liu Hui
-
John Wallis (1616-1703)
-
Construcción aproximada para la cuadratura del círculo, encontrada por Ramanujan
-
Representación del experimento en el modelo de la «aguja de Buffon»
-
Representación geométrica de la fórmula de Euler
Véase también
 En inglés: Pi Facts for Kids
En inglés: Pi Facts for Kids



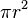 , donde r es el radio.
, donde r es el radio.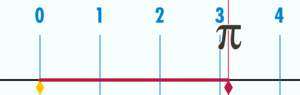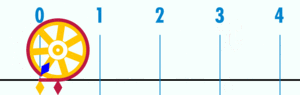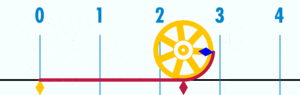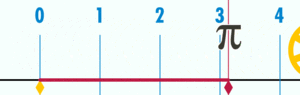
 es la relación entre la longitud de una
es la relación entre la longitud de una