Topología para niños
La topología es una rama de las matemáticas que estudia las propiedades de los objetos que no cambian cuando los estiramos, doblamos, encogemos o retorcemos, siempre que no los rompamos ni los peguemos. Imagina que los objetos están hechos de una goma muy elástica.
Esta disciplina se enfoca en ideas como la "cercanía" entre puntos, la cantidad de "agujeros" que tiene un objeto, o cómo de "consistente" es su forma. Ayuda a comparar objetos y a clasificarlos según características como si están "conectados" (de una sola pieza) o si son "compactos" (como si no tuvieran bordes sueltos).
Los matemáticos usan la palabra topología de dos maneras. Una es la que acabamos de explicar, de forma más general. La otra es más formal y se refiere a un conjunto específico de reglas que se aplican a grupos de elementos, como si fueran piezas de un rompecabezas.
Contenido
¿Qué es la topología de forma sencilla?
La "geometría de la página de goma"
Piensa en la topología como la "geometría de la página de goma". En la geometría euclídea (la que estudias en la escuela), dos figuras son iguales si puedes mover una sobre la otra sin cambiar su tamaño ni su forma. Por ejemplo, un cuadrado es igual a otro cuadrado si tienen el mismo tamaño.
Pero en topología, dos objetos son equivalentes de una forma mucho más flexible. Puedes estirarlos, encogerlos o doblarlos. Lo único que no puedes hacer es romperlos o cortar lo que está unido, ni pegar lo que está separado.
Por ejemplo, un triángulo y una circunferencia son lo mismo en topología. Puedes estirar un triángulo hasta que se vea como un círculo sin romperlo. Sin embargo, una circunferencia no es lo mismo que un segmento de línea. Para convertir una en otra, tendrías que cortar la circunferencia o pegar sus extremos.
Por eso se le llama la "geometría de la página de goma". Es como si estudiáramos las formas en un papel elástico que puede cambiar de tamaño y forma.

Un chiste común entre los topólogos (los matemáticos que estudian topología) es que "un topólogo no puede distinguir una taza de una rosquilla". Esto se debe a que, si la taza tiene un asa, tanto la taza como la rosquilla tienen un solo agujero. Si puedes deformar una taza de café con asa hasta convertirla en una rosquilla sin romperla, ¡son topológicamente iguales!
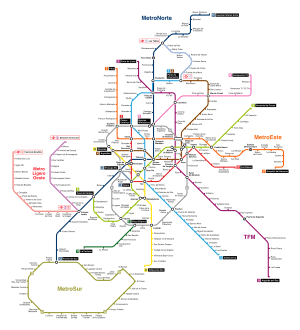
Un ejemplo práctico: el mapa del metro
Mira un mapa del metro de Madrid. En él, ves las estaciones y las líneas que las conectan. Pero el mapa no es exacto en cuanto a las distancias o las curvas reales de las vías. Las líneas no tienen la longitud real a escala, ni las estaciones están en su posición exacta.
Aun así, este mapa es muy útil. ¿Por qué? Porque representa fielmente la información que necesitas para viajar: la "información topológica". Te dice qué estaciones están conectadas y en qué orden, sin importar las distancias exactas. Es un ejemplo perfecto de cómo la topología se enfoca en las conexiones y no en las medidas precisas.
Historia de la topología
Las primeras ideas relacionadas con la topología surgieron hace mucho tiempo, con conceptos como el de "límite" en las matemáticas. Los antiguos griegos, como Arquímedes, ya usaban métodos que se acercaban a estas ideas.
La necesidad de entender mejor la "cercanía" y la "continuidad" en las matemáticas se hizo más clara en el siglo XVII, con el desarrollo del cálculo infinitesimal.
Se dice que la topología moderna comenzó con Euler en 1735. Él resolvió el famoso problema de los puentes de Königsberg. Este problema consistía en saber si era posible cruzar los siete puentes de la ciudad de Königsberg (hoy Kaliningrado) pasando por cada uno una sola vez. La forma en que Euler lo resolvió fue puramente topológica, centrándose en las conexiones y no en las distancias.
El término topología fue usado por primera vez por Johann Benedict Listing en 1836. Antes, a esta rama se le llamaba analysis situs. Más tarde, en 1906, Maurice Fréchet introdujo el concepto de espacio métrico, que ayuda a definir la distancia entre puntos.
| Año | Acontecimiento |
|---|---|
| 300 a. C. | Euclides estudia formas básicas como los poliedros regulares, que son importantes para los topólogos. |
| 250 a. C. | Arquímedes investiga curvas y formas tridimensionales. |
| 1735 d. C. | Leonhard Euler resuelve el problema de los puentes de Königsberg, un hito en la topología. |
| 1858 | August Möbius y Johann Benedict Listing descubren la banda de Möbius, una superficie con una sola cara. |
| 1890 | Giuseppe Peano demuestra que un cuadrado relleno puede ser considerado una curva. |
| Década de 1920 | Pável Urysón y Karl Menger definen el concepto de curva usando la topología. |
Conceptos básicos de la topología
La topología se basa en la idea de "proximidad" o "cercanía". Aunque parezca algo que se siente, la topología le da una definición muy precisa.
Para entenderlo, imaginemos un conjunto de cosas, al que llamamos "espacio". Cada cosa en ese espacio es un "punto". Un "entorno" de un punto es un grupo de puntos que están cerca de él.
Una "topología" es una forma de decidir qué grupos de puntos son "abiertos". Estos grupos abiertos deben cumplir ciertas reglas:
- El espacio completo y un grupo vacío (sin puntos) son siempre abiertos.
- Si unes varios grupos abiertos, el resultado también es un grupo abierto.
- Si cruzas (intersecas) un número limitado de grupos abiertos, el resultado también es un grupo abierto.
Cuando tenemos un espacio y una topología definida en él, a eso lo llamamos un espacio topológico.
¿Qué es un espacio métrico?
A veces, podemos definir la cercanía usando una "distancia". Un espacio métrico es un espacio donde podemos medir la distancia entre dos puntos. Esta distancia debe cumplir algunas reglas, como que siempre es positiva, la distancia de A a B es la misma que de B a A, y la distancia más corta entre dos puntos es una línea recta (la desigualdad del triángulo).
Si tenemos una distancia, podemos definir los grupos "abiertos" como "bolas abiertas". Una bola abierta es el conjunto de todos los puntos que están a una cierta distancia de un punto central.
Conjuntos conectados
Un conjunto es conexo si está "hecho de una sola pieza". Es decir, no puedes dividirlo en dos partes separadas que no se toquen. Por ejemplo, una bola de hierro es conexa.
Un conjunto es conexo por caminos si puedes ir de cualquier punto a cualquier otro punto dentro del conjunto sin salirte de él, siguiendo un camino continuo. Si un conjunto es conexo por caminos, también es conexo.
Imagina una esponja o una rejilla. Son conjuntos conexos, pero tienen agujeros. La topología algebraica nos ayuda a entender cuántos agujeros tiene un objeto y cómo están conectados.
Compacidad
Los conjuntos compactos son un poco más complejos de entender. En un espacio donde se puede medir la distancia, un conjunto compacto es aquel que está "cerrado" (contiene todos sus bordes) y "acotado" (puedes encerrarlo dentro de una bola de cierto tamaño). La compacidad es una propiedad muy importante en topología.
Continuidad
Una aplicación continua (o función continua) es como una transformación que no "rompe" lo que está unido ni "pega" lo que está separado. Si tienes puntos cercanos en el espacio original, la función los transforma en puntos que también están cercanos en el espacio de llegada.
Ramas de la topología
La topología se divide principalmente en tres ramas:
- La topología general o conjuntista: Es la base, donde se definen los conceptos fundamentales como los espacios topológicos y los entornos.
- La topología algebraica: Usa herramientas del álgebra para estudiar las propiedades de los espacios, como la cantidad de "agujeros" o la "porosidad". Aquí se estudia la teoría de nudos.
- La topología diferencial: Combina la topología con el cálculo diferencial para estudiar formas suaves y sus propiedades.
La topología tiene aplicaciones en muchas otras áreas de las matemáticas, como el análisis matemático, la teoría de grafos y la geometría fractal. Incluso se usa en campos como la biología y la sociología.
Galería de imágenes
Véase también
 En inglés: Topology Facts for Kids
En inglés: Topology Facts for Kids