Papiro de Ahmes para niños
El Papiro de Ahmes, también conocido como Papiro Matemático Rhind, es un documento muy antiguo que contiene muchos problemas de matemáticas. Fue escrito en hierático, una forma de escritura del antiguo Egipto, y mide unos seis metros de largo por 35 centímetros de ancho. Se encuentra en muy buen estado de conservación.
Este papiro fue copiado por un escriba llamado Ahmes durante el reinado de Apofis I. El texto original, del cual Ahmes hizo esta copia, es aún más antiguo, de la época del faraón Amenemhat III, hace más de 3.500 años.
Muchos expertos han estudiado este papiro. El egiptólogo alemán August Eisenlohr fue el primero en publicarlo y analizarlo. Después, otros investigadores como Peet, Griffith, Chace, Robins y Shute también publicaron sus estudios sobre este importante documento matemático.
Contenido
Historia del Papiro Rhind
El escriba Ahmes escribió este papiro a mediados del siglo XVI antes de Cristo. Él mismo menciona al principio del texto que se basó en escritos que tenían unos trescientos años de antigüedad.
El papiro fue descubierto en el siglo XIX cerca de las ruinas de un antiguo edificio llamado Ramesseum. En 1858, un coleccionista llamado Henry Rhind lo compró. Cuando Henry Rhind falleció en 1864, el papiro fue donado al Museo Británico en Londres, junto con otro documento llamado el rollo de cuero matemático egipcio.
Lamentablemente, cuando se encontró, el papiro estaba dividido en dos partes y le faltaba una sección central de unos 18 centímetros. Se cree que pudo haber sido cortado por ladrones para venderlo por más dinero. Sin embargo, en 1922, se encontraron por casualidad varios fragmentos de la parte perdida en la colección de la Sociedad Histórica de Nueva York. Estos fragmentos fueron muy importantes para entender la obra completa.
El documento está formado por 14 láminas, cada una de unos 40 por 32 centímetros. Las partes principales del papiro (EA 10057 y EA 10058) están en el Museo Británico, aunque no siempre están expuestas al público. Los fragmentos que se recuperaron de la sección perdida (37.1784E) se guardan en el Museo de Brooklyn.
Contenido Matemático del Papiro
El papiro de Ahmes contiene 87 problemas de matemáticas. Estos problemas tratan sobre temas como:
- Operaciones básicas con números enteros y fracciones.
- Cómo resolver ecuaciones sencillas.
- Problemas de "adivinar un número".
- Cálculo de áreas de figuras planas.
- Cálculo de volúmenes de objetos.
- Progresiones (series de números que siguen un patrón).
- Repartos proporcionales.
- La regla de tres.
- Conceptos básicos de trigonometría.
Tipos de Problemas
Los problemas se pueden clasificar en varias categorías:
- Operaciones con números: Problemas del 1 al 23, 47, 80 y 81.
- Ecuaciones simples: Problemas del 24 al 27 y del 30 al 38.
- Problemas de lógica: Los problemas 28 y 29.
- Progresiones aritméticas: Problemas 39, 40 y 64.
- Cálculo de volúmenes: Problemas del 41 al 46 y del 56 al 60.
- Cálculo de áreas: Problemas del 48 al 55.
- Reglas especiales: Los problemas 61 y 61B, que enseñan a obtener dos tercios de números pares.
- Proporciones: Problemas 62, 63 y del 65 al 68.
- Progresiones geométricas: El problema 79.
- Otros problemas: Del 80 al 87.
Las Fracciones Egipcias
En el papiro se explica cómo los antiguos egipcios trabajaban con las fracciones. A diferencia de nosotros, que usamos fracciones como 3/4 o 5/8, los egipcios escribían las fracciones como una suma de "fracciones unitarias". Una fracción unitaria es aquella que tiene un 1 en la parte de arriba (el numerador), como 1/2, 1/3 o 1/5. Por ejemplo, para ellos, 3/4 se escribiría como 1/2 + 1/4. Este tipo de sumas se conocen hoy como fracciones egipcias.
El Valor de Pi
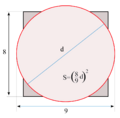
Un ejemplo interesante es el problema 50. En él, se dice que el área de un círculo con un diámetro de 9 unidades es igual al área de un cuadrado con un lado de 8 unidades.
Si usamos la fórmula moderna para el área de un círculo (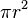
) y la comparamos con lo que dice el papiro, podemos ver que los egipcios tenían una muy buena aproximación del valor de pi (
), aunque no lo conocían como tal.
Según el papiro, el área del círculo es igual al área de un cuadrado cuyo lado es 8/9 del diámetro del círculo. Esto significa que: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left ( \frac{8}{9} \times \text{diámetro} \right)^2 = \left ( \frac{8}{9} \times 2 \times \text{radio} \right)^2 = \left ( \frac{16}{9} \times \text{radio} \right)^2 = \frac{256}{81} \times \text{radio}^2
El valor de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{256}{81} es aproximadamente 3.160493. Esto es muy cercano al valor real de , que es aproximadamente 3.141592. ¡Es una aproximación bastante precisa para una época tan antigua!
Galería de imágenes
-
Papiro de Ahmes o papiro Rhind.
-
Detalle.
-
El área del círculo es igual a la del cuadrado cuyo lado vale los 8/9 del diámetro de aquel. (problema 50)
.png)
.png)
Véase también
En inglés: Rhind Mathematical Papyrus Facts for Kids
