robot de la enciclopedia para niños

Tabla de multiplicar para niños

Enciclopedia para niños
Archivo:Multiplication table to scale
Tabla de multiplicar del 1 al 10 dibujada a escala con la mitad superior derecha etiquetada con factorizaciones de primos.

Las tablas de multiplicar son herramientas muy importantes en matemáticas. Nos ayudan a entender cómo funciona la multiplicación y a encontrar rápidamente el resultado de multiplicar dos números. Son como un mapa que muestra el "producto" (el resultado de la multiplicación) de diferentes combinaciones de números.

En la escuela, aprendemos las tablas de multiplicar memorizando los resultados de multiplicar un número (generalmente del 1 al 10) por otros números (del 0 al 10). Una vez que conoces estas tablas, puedes multiplicar números grandes o con decimales usando un método llamado Algoritmo de multiplicación.

La tabla de multiplicar es una parte fundamental de la aritmética en el Sistema de numeración decimal, que es el sistema de números que usamos todos los días. Muchos maestros creen que es muy útil memorizar las tablas hasta el 9 × 9 para tener una base sólida en matemáticas.

Historia de las Tablas de Multiplicar

Orígenes Antiguos de las Tablas

Archivo:Qinghuajian, Suan Biao
Una tabla de multiplicación decimal china de tiras de bambú, del año 305 a.C.

Las primeras tablas de multiplicar que conocemos fueron usadas por los matemáticos babilonios hace unos 4000 años. Sin embargo, ellos usaban un sistema de números diferente, basado en el 60. Las tablas más antiguas que usan el sistema de base 10 (el que usamos nosotros) son las chinas. Se encontraron en unas tiras de bambú llamadas Tsinghua Bamboo Slips y datan de alrededor del año 305 a.C., durante un periodo antiguo de China.

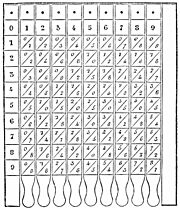
Archivo:PSM V26 D467 Table of pythagoras on slats
"Tabla de Pitágoras" en huesos de Napier

A veces, la tabla de multiplicar se asocia con el antiguo matemático griego Pitágoras (quien vivió entre el 570 y el 495 a.C.). Por eso, en muchos idiomas (como el francés o el italiano), se le llama la "Tabla de Pitágoras". Un matemático grecorromano llamado Nicómaco (del 60 al 120 d.C.) incluyó una tabla de multiplicar en su libro Introducción a la aritmética. La tabla de multiplicar griega más antigua que se ha encontrado está en una tablilla de cera del siglo I d.C. y se guarda en el Museo Británico.

En el año 493 d.C., un matemático llamado Victorio de Aquitania creó una tabla de multiplicar muy grande, con 98 columnas. Mostraba el producto de números del 2 al 50, y también incluía fracciones.

Las Tablas en la Época Moderna

En 1820, el matemático John Leslie publicó un libro donde mostraba una tabla de multiplicar que llegaba hasta 99 × 99. Él incluso sugería que los estudiantes memorizaran las tablas hasta 50 × 50.

Hoy en día, en muchos países de habla inglesa, es común usar una tabla de multiplicar que llega hasta 12 × 12.

× 0 1 2 3 4 5 6 7 8 9 10 11 12
0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7 8 9 10 11 12
2 0 2 4 6 8 10 12 14 16 18 20 22 24
3 0 3 6 9 12 15 18 21 24 27 30 33 36
4 0 4 8 12 16 20 24 28 32 36 40 44 48
5 0 5 10 15 20 25 30 35 40 45 50 55 60
6 0 6 12 18 24 30 36 42 48 54 60 66 72
7 0 7 14 21 28 35 42 49 56 63 70 77 84
8 0 8 16 24 32 40 48 56 64 72 80 88 96
9 0 9 18 27 36 45 54 63 72 81 90 99 108
10 0 10 20 30 40 50 60 70 80 90 100 110 120
11 0 11 22 33 44 55 66 77 88 99 110 121 132
12 0 12 24 36 48 60 72 84 96 108 120 132 144

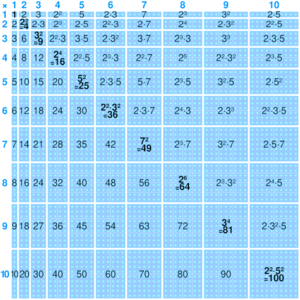
En China, como el orden de los números no cambia el resultado de la multiplicación (propiedad conmutativa), muchas escuelas usan una tabla más pequeña. Algunas incluso quitan la primera columna, ya que multiplicar por 1 siempre da el mismo número.

1 1
2 2 4
3 3 6 9
4 4 8 12 16
5 5 10 15 20 25
6 6 12 18 24 30 36
7 7 14 21 28 35 42 49
8 8 16 24 32 45 48 56 64
9 9 18 27 36 45 54 63 72 81
× 1 2 3 4 5 6 7 8 9

La forma tradicional de aprender las tablas era memorizar cada columna, por ejemplo:

   1 × 10 = 10
   2 × 10 = 20
   3 × 10 = 30
   4 × 10 = 40
   5 × 10 = 50
   6 × 10 = 60
   7 × 10 = 70
   8 × 10 = 80
   9 × 10 = 90

Esta manera de escribir las tablas en columnas con las operaciones completas todavía se usa en algunos países.

Cómo se Organizan las Tablas de Multiplicar

La forma más común de ver las tablas de multiplicar para aprenderlas es en forma de lista. En estas listas, se multiplica un número (del 1 al 10 o del 0 al 10) por cada número de la secuencia.

\begin{array}{c} tabla \; de \; multiplicar \\ \\ \begin{array}{ccccc} \begin{array}{|c|} \hline tabla \; del \; 1 \\ \begin{array}{rcrcr} 1 & \times & 0 & = & 0 \\ 1 & \times & 1 & = & 1 \\ 1 & \times & 2 & = & 2 \\ 1 & \times & 3 & = & 3 \\ 1 & \times & 4 & = & 4 \\ 1 & \times & 5 & = & 5 \\ 1 & \times & 6 & = & 6 \\ 1 & \times & 7 & = & 7 \\ 1 & \times & 8 & = & 8 \\ 1 & \times & 9 & = & 9 \\ 1 & \times & 10 & = & 10 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 2 \\ \begin{array}{rcrcr} 2 & \times & 0 & = & 0 \\ 2 & \times & 1 & = & 2 \\ 2 & \times & 2 & = & 4 \\ 2 & \times & 3 & = & 6 \\ 2 & \times & 4 & = & 8 \\ 2 & \times & 5 & = & 10 \\ 2 & \times & 6 & = & 12 \\ 2 & \times & 7 & = & 14 \\ 2 & \times & 8 & = & 16 \\ 2 & \times & 9 & = & 18 \\ 2 & \times & 10 & = & 20 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 3 \\ \begin{array}{rcrcr} 3 & \times & 0 & = & 0 \\ 3 & \times & 1 & = & 3 \\ 3 & \times & 2 & = & 6 \\ 3 & \times & 3 & = & 9 \\ 3 & \times & 4 & = & 12 \\ 3 & \times & 5 & = & 15 \\ 3 & \times & 6 & = & 18 \\ 3 & \times & 7 & = & 21 \\ 3 & \times & 8 & = & 24 \\ 3 & \times & 9 & = & 27 \\ 3 & \times & 10 & = & 30 \\ \end{array} \\ \hline \end{array} \\ \\ \begin{array}{|c|} \hline tabla \; del \; 4 \\ \begin{array}{rcrcr} 4 & \times & 0 & = & 0 \\ 4 & \times & 1 & = & 4 \\ 4 & \times & 2 & = & 8 \\ 4 & \times & 3 & = & 12 \\ 4 & \times & 4 & = & 16 \\ 4 & \times & 5 & = & 20 \\ 4 & \times & 6 & = & 24 \\ 4 & \times & 7 & = & 28 \\ 4 & \times & 8 & = & 32 \\ 4 & \times & 9 & = & 36 \\ 4 & \times & 10 & = & 40\\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 5 \\ \begin{array}{rcrcr} 5 & \times & 0 & = & 0 \\ 5 & \times & 1 & = & 5 \\ 5 & \times & 2 & = & 10 \\ 5 & \times & 3 & = & 15 \\ 5 & \times & 4 & = & 20 \\ 5 & \times & 5 & = & 25 \\ 5 & \times & 6 & = & 30 \\ 5 & \times & 7 & = & 35 \\ 5 & \times & 8 & = & 40 \\ 5 & \times & 9 & = & 45 \\ 5 & \times & 10 & = & 50 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 6 \\ \begin{array}{rcrcr} 6 & \times & 0 & = & 0 \\ 6 & \times & 1 & = & 6 \\ 6 & \times & 2 & = & 12 \\ 6 & \times & 3 & = & 18 \\ 6 & \times & 4 & = & 24 \\ 6 & \times & 5 & = & 30 \\ 6 & \times & 6 & = & 36 \\ 6 & \times & 7 & = & 42 \\ 6 & \times & 8 & = & 48 \\ 6 & \times & 9 & = & 54 \\ 6 & \times & 10 & = & 60 \\ \end{array} \\ \hline \end{array} \\ \\ \begin{array}{|c|} \hline tabla \; del \; 7 \\ \begin{array}{rcrcr} 7 & \times & 0 & = & 0 \\ 7 & \times & 1 & = & 7 \\ 7 & \times & 2 & = & 14 \\ 7 & \times & 3 & = & 21 \\ 7 & \times & 4 & = & 28 \\ 7 & \times & 5 & = & 35 \\ 7 & \times & 6 & = & 42 \\ 7 & \times & 7 & = & 49 \\ 7 & \times & 8 & = & 56 \\ 7 & \times & 9 & = & 63 \\ 7 & \times & 10 & = & 70 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 8 \\ \begin{array}{rcrcr} 8 & \times & 0 & = & 0 \\ 8 & \times & 1 & = & 8 \\ 8 & \times & 2 & = & 16 \\ 8 & \times & 3 & = & 24 \\ 8 & \times & 4 & = & 32 \\ 8 & \times & 5 & = & 40 \\ 8 & \times & 6 & = & 48 \\ 8 & \times & 7 & = & 56 \\ 8 & \times & 8 & = & 64 \\ 8 & \times & 9 & = & 72 \\ 8 & \times & 10 & = & 80 \\ \end{array} \\ \hline \end{array} & \begin{array}{|c|} \hline tabla \; del \; 9 \\ \begin{array}{rcrcr} 9 & \times & 0 & = & 0 \\ 9 & \times & 1 & = & 9 \\ 9 & \times & 2 & = & 18 \\ 9 & \times & 3 & = & 27 \\ 9 & \times & 4 & = & 36 \\ 9 & \times & 5 & = & 45 \\ 9 & \times & 6 & = & 54 \\ 9 & \times & 7 & = & 63 \\ 9 & \times & 8 & = & 72 \\ 9 & \times & 9 & = & 81 \\ 9 & \times & 10 & = & 90 \\ \end{array} \\ \hline \end{array} \\ \end{array} \\ \end{array}

La Tabla Pitagórica: Una Forma Diferente de Ver las Multiplicaciones

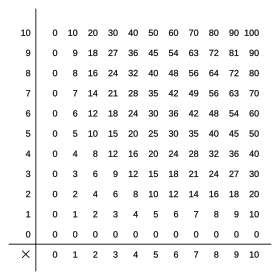
Tabla de muitiplicar 11.svg

Otra manera de organizar la tabla de multiplicar es la tabla pitagórica. Se llama así en honor a Pitágoras. Esta tabla se parece a una cuadrícula. La primera fila y la primera columna tienen los números que vamos a multiplicar (normalmente hasta el 10). En cada cuadro donde se cruzan una fila y una columna, encuentras el resultado de multiplicar el número de esa fila por el número de esa columna.

Esta tabla es más compacta y nos ayuda a ver algunas propiedades interesantes de la multiplicación. Por ejemplo, puedes notar la propiedad conmutativa, que significa que el orden de los números no cambia el resultado (por ejemplo, 5 × 3 es lo mismo que 3 × 5). Esto hace que la tabla sea "simétrica": los números a un lado y otro de la línea diagonal que va del 1 al 100 son iguales.

También puedes ver esta simetría si comparas una fila con su columna correspondiente. Por ejemplo, la fila del 3 tiene los números 3, 6, 9, 12... y la columna del 3 tiene la misma secuencia. Esto ocurre porque, al cambiar filas por columnas, la tabla no cambia gracias a la propiedad conmutativa.

La línea diagonal principal de la tabla muestra los cuadrados de los números (un número multiplicado por sí mismo), como 1x1=1, 2x2=4, 3x3=9, etc. Los números alrededor de esta diagonal también se distribuyen de forma simétrica.

Otros Métodos y Tablas de Multiplicar

Archivo:Abaco de Napier (tablero y varillas)
Ábaco neperiano.

Para mejorar el cálculo mental, algunas personas aprenden tablas de multiplicar con números más grandes que el 10.

En el antiguo Egipto, usaban un método llamado multiplicación por duplicación. Con este método, no necesitabas memorizar tablas, solo saber sumar para resolver multiplicaciones y divisiones.

En la antigua Babilonia, que usaba un sistema basado en el número 60, se usaban muchas tablillas con productos de números, incluso no enteros, multiplicados por 2, 3, 4, hasta 60.

Las tablas de multiplicar también se usan en matemáticas más avanzadas para definir operaciones en sistemas especiales como grupos o cuerpos.

Hoy en día, existen métodos más sencillos para aprender las tablas de multiplicar. Estos métodos buscan reducir la cantidad de resultados que hay que memorizar, haciendo el aprendizaje más fácil y rápido.

Galería de imágenes

  • Multiplication table to scale

    Tabla de multiplicar del 1 al 10 dibujada a escala con la mitad superior derecha etiquetada con factorizaciones de primos.

  • Qinghuajian, Suan Biao

    Una tabla de multiplicación decimal china de tiras de bambú, del año 305 a.C.

  • PSM V26 D467 Table of pythagoras on slats

    "Tabla de Pitágoras" en huesos de Napier

  • Abaco de Napier (tablero y varillas)

    Ábaco neperiano.

Véase también

Kids robot.svg En inglés: Multiplication table Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Tabla_de_multiplicar&oldid=4979175»
kids search engine
Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:
Tabla de multiplicar para Niños. Enciclopedia Kiddle.