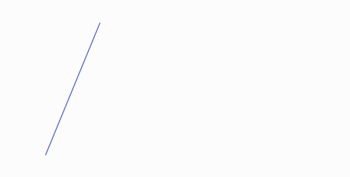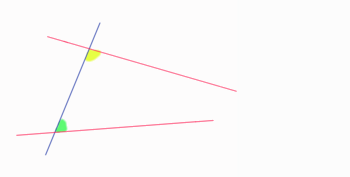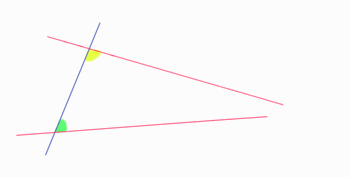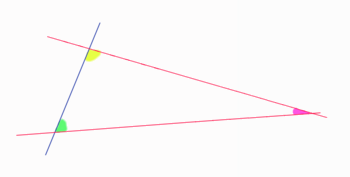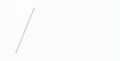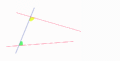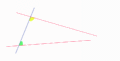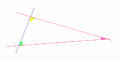Quinto postulado de Euclides para niños
El postulado de las paralelas o quinto postulado de Euclides es una de las reglas fundamentales del libro Los Elementos, escrito por el matemático griego Euclides alrededor del año 300 a.C. Este postulado es muy importante porque define un tipo especial de geometría, llamada geometría euclidiana.
La geometría euclidiana es el estudio de las formas y el espacio que sigue todas las reglas de Euclides, incluyendo este quinto postulado. Si una geometría no cumple con el quinto postulado, se le llama geometría no euclidiana. Hay otra rama, la geometría absoluta, que solo usa los primeros cuatro postulados de Euclides, sin depender del quinto.
Contenido
¿Qué dice el Quinto Postulado de Euclides?
El quinto postulado de Euclides es un poco largo de entender, pero su idea principal es sencilla. Imagina una línea recta que cruza otras dos líneas rectas. Si los ángulos que se forman en un lado de la línea que cruza son menores que dos ángulos rectos (es decir, menos de 180 grados), entonces esas dos líneas se encontrarán si las prolongamos lo suficiente en ese mismo lado.
Otras formas de entender el Quinto Postulado
A lo largo de la historia, los matemáticos han encontrado otras maneras de explicar la misma idea que el quinto postulado. Aquí te mostramos algunas de las más conocidas:
- La suma de los ángulos de un triángulo: Si sumas los ángulos de cualquier triángulo, el resultado siempre será igual a la suma de dos ángulos rectos (180 grados). Esta idea ya se conocía en tiempos de Aristóteles.
- Rectas paralelas y distancia: Las rectas paralelas siempre mantienen la misma distancia entre sí. Esto significa que nunca se acercan ni se alejan.
- Una sola paralela por un punto: Si tienes una línea recta y un punto fuera de ella, solo puedes dibujar una única línea recta que pase por ese punto y sea paralela a la primera. Esta es una de las formulaciones más famosas y se conoce como el «postulado de las paralelas» o axioma de Playfair.
- Triángulos semejantes: Siempre es posible construir un triángulo que sea similar a otro triángulo dado, sin importar su tamaño.
¿Es un axioma o un teorema?
Euclides presentó el quinto postulado como un axioma. Un axioma es una afirmación que se acepta como verdadera sin necesidad de demostración. Los primeros cuatro postulados de Euclides son bastante simples:
- Se puede dibujar una línea recta entre dos puntos cualquiera.
- Una línea recta finita se puede extender indefinidamente en línea recta.
- Se puede dibujar un círculo con cualquier centro y cualquier radio.
- Todos los ángulos rectos son iguales entre sí.
- El quinto postulado (el de las paralelas) es el más complejo de todos.
Euclides mismo no usó el quinto postulado en sus primeras 28 demostraciones, como si supiera que era diferente o más difícil. Durante más de 2000 años, muchos matemáticos intentaron demostrar que el quinto postulado podía deducirse de los otros cuatro. Pensaban que no era un axioma, sino un teorema (una afirmación que se puede probar).
Matemáticos como Omar Jayam y Nasir al-Din al-Tusi en el mundo árabe, y más tarde Giovanni Gerolamo Saccheri en Italia, intentaron demostrarlo. Saccheri, por ejemplo, intentó probarlo asumiendo lo contrario y buscando una contradicción. Aunque tuvo algunos éxitos, no logró demostrarlo completamente.
La independencia del Quinto Postulado y las Geometrías No Euclidianas
Después de 22 siglos, se llegó a una conclusión sorprendente: el quinto postulado es independiente de los otros cuatro. Esto significa que no se puede demostrar a partir de ellos. Esta idea abrió la puerta a la existencia de otras geometrías donde este postulado no se cumple.
Para entender esto, debemos pensar en las definiciones de Euclides de lo que es una línea y un plano. Por ejemplo:
- Una línea es una longitud sin ancho.
- Una línea recta es aquella que se extiende de manera uniforme entre sus puntos.
- Un plano es una superficie que solo tiene largo y ancho.
- Las rectas paralelas son líneas en el mismo plano que, aunque se prolonguen indefinidamente, nunca se encuentran.
Si cambiamos nuestra idea de "plano", podemos ver cómo el quinto postulado podría no cumplirse. Por ejemplo, si consideramos la superficie de una esfera como nuestro "plano", y las "líneas rectas" son los círculos más grandes que se pueden dibujar en ella (como el ecuador en un globo terráqueo), entonces por un punto fuera de una "línea recta" no pasaría ninguna "línea recta" paralela a la dada. Todas las "líneas rectas" en una esfera se cruzan en dos puntos.
El nacimiento de las Geometrías No Euclidianas
En el siglo XIX, los matemáticos János Bolyai y Nikolai Ivanovich Lobachevsky (y también Carl Friedrich Gauss, aunque no publicó sus hallazgos) demostraron de forma independiente que el quinto postulado es independiente.
Su idea fue la siguiente: si el quinto postulado dependiera de los otros, al negarlo y añadir esa negación a los otros cuatro postulados, se llegaría a una contradicción lógica. Sin embargo, al hacer esto, no encontraron ninguna contradicción. Esto significaba que las geometrías que se obtenían al negar el quinto postulado eran lógicamente válidas.
Existen diferentes formas de negar el quinto postulado, lo que dio origen a distintas geometrías no euclidianas:
- Si se asume que por un punto exterior a una recta no pasa ninguna paralela, se obtiene la geometría esférica.
- Si se asume que pasan infinitas paralelas, se obtiene la geometría hiperbólica (la de Lobachevsky).
El Quinto Postulado en la Geometría Actual
Hoy en día, la geometría ha evolucionado mucho. Los matemáticos usan herramientas como la topología, el análisis y el álgebra para estudiar los espacios. Ya no es el objetivo principal saber si un espacio cumple o no el quinto postulado de Euclides. Aunque es un tema importante para entender la historia de las matemáticas, ahora se estudian propiedades más complejas, como la curvatura de un espacio. El problema del quinto postulado fue un gran impulso para el desarrollo de la geometría, pero ahora se ve más como un tema introductorio.
Historia de la búsqueda del Quinto Postulado
Durante todo el siglo XVIII, hubo un gran esfuerzo por demostrar el quinto postulado de Euclides a partir de los otros cuatro. Todos estos intentos no tuvieron éxito, precisamente porque el quinto postulado no se puede deducir de ellos.
Las primeras pruebas publicadas de que el quinto postulado era independiente fueron los modelos de geometría hiperbólica de János Bolyai (1832) y Nikolái Lobachevski (1829). Ellos llegaron a sus conclusiones de forma independiente. Más tarde, se descubrió que Carl Friedrich Gauss también había desarrollado una construcción de la geometría hiperbólica, pero nunca la publicó.
Es interesante notar que, aunque trabajaron por separado, había conexiones entre ellos. Johann Christian Martin Bartels, tutor de Gauss, pudo haberle introducido en el problema del quinto postulado. Más tarde, Bartels fue profesor de Lobachevski. Además, el padre de János Bolyai, Farkas Bolyai, era amigo de Gauss y habían discutido el quinto postulado. A pesar de que su padre le aconsejó no investigar el problema, János desobedeció y encontró su propia solución.
Galería de imágenes
Véase también
 En inglés: Parallel postulate Facts for Kids
En inglés: Parallel postulate Facts for Kids