Análisis matemático para niños
El análisis matemático es una rama de las matemáticas que estudia los conjuntos numéricos como los números reales y los números complejos. También se enfoca en las funciones entre estos conjuntos y otras construcciones relacionadas. Esta área de las matemáticas comenzó a desarrollarse cuando se empezó a definir de forma precisa el concepto de límite. El análisis matemático explora ideas como la continuidad, la integración y la derivación.
Una diferencia importante entre el álgebra y el análisis es que el análisis a menudo trabaja con secuencias de un número infinito de elementos. En cambio, el álgebra generalmente se ocupa de cantidades finitas.
Contenido
Historia del Análisis Matemático
Orígenes Antiguos del Análisis
Desde la Edad Antigua, matemáticos como los griegos Eudoxo de Cnidos y Arquímedes usaron ideas que se parecen a los conceptos de límite y convergencia. Ellos emplearon el "método de agotamiento" para calcular áreas y volúmenes de figuras y sólidos. Por ejemplo, el número π se aproximó usando este método.
En la India, en el siglo XII, el matemático Bhaskara desarrolló ideas que hoy conocemos como parte del cálculo diferencial, incluyendo un concepto similar al teorema de Rolle.
Avances en la Edad Media
En el siglo V, el matemático chino Zu Chongzhi usó un método para encontrar el volumen de una esfera, similar al Principio de Cavalieri.
Más tarde, en el siglo XIV, el matemático indio Madhava de Sangamagrama hizo descubrimientos fundamentales. Desarrolló ideas como las series infinitas, las series de potencias y las series de Taylor. También trabajó con las series de Taylor para funciones trigonométricas (seno, coseno, tangente) y estimó los errores al usar estas series. Sus alumnos de la Escuela de Kerala continuaron su trabajo hasta el siglo XVI.
El Nacimiento del Cálculo Moderno
Los fundamentos modernos del análisis matemático se establecieron en Europa en el siglo XVII. Matemáticos como Descartes y Fermat desarrollaron la geometría analítica, que fue un paso importante hacia el cálculo moderno.
Unas décadas después, Newton y Leibniz crearon de forma independiente el cálculo. Esta nueva herramienta matemática fue muy importante y se aplicó en muchos campos, como el cálculo de variaciones y las ecuaciones diferenciales.
La Modernización del Análisis
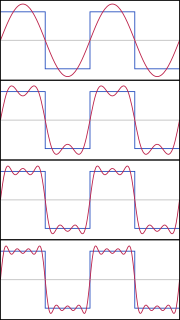
A lo largo del siglo XVIII, los matemáticos debatieron sobre la definición de función. En el siglo XIX, Cauchy sentó las bases lógicas del cálculo usando el concepto de sucesión de Cauchy. También inició la teoría formal del análisis complejo. Otros matemáticos como Poisson, Liouville y Fourier estudiaron las ecuaciones en derivadas parciales y el análisis de Fourier.
A mediados del siglo XIX, Riemann introdujo su teoría de la integración. Más tarde, Weierstrass desarrolló una definición muy precisa de límite (la definición ε - δ). Esto llevó a los matemáticos a preguntarse sobre la existencia de los números reales. Dedekind construyó los números reales usando las "cortaduras de Dedekind".
A principios del siglo XX, el cálculo se formalizó aún más usando la teoría de conjuntos. Lebesgue resolvió el problema de la medida, y Hilbert introdujo los espacios de Hilbert para resolver ecuaciones integrales. En los años 1920, Banach creó el análisis funcional.
Conceptos Clave del Análisis
¿Qué es un Espacio Métrico?
Un espacio métrico es un conjunto de elementos donde se puede definir una "distancia" entre ellos. Esta distancia se llama métrica.
Gran parte del análisis matemático se realiza en espacios métricos. Los más comunes son la recta real, el plano complejo y el espacio euclidiano.
Formalmente, un espacio métrico es un par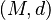 
, donde 
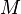es un conjunto y 
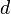es una función que mide la distancia entre dos puntos. Esta función debe cumplir ciertas reglas, como que la distancia de un punto a sí mismo es cero, la distancia de A a B es la misma que de B a A, y la distancia más corta entre dos puntos es una línea recta (la Desigualdad triangular).
Secuencias y Límites
Una secuencia es una lista ordenada de elementos. A diferencia de un conjunto, el orden de los elementos importa y pueden repetirse. Una secuencia se puede ver como una función donde el orden es importante.
Una propiedad muy importante de una secuencia es la convergencia. De manera sencilla, una secuencia converge si se acerca a un punto específico, llamado su límite, a medida que la secuencia se hace muy larga. Es decir, la distancia entre los elementos de la secuencia y el límite se vuelve cada vez más pequeña.
Ramas Principales del Análisis
Análisis Real
El análisis real se enfoca en los números reales y las funciones que trabajan con ellos. Estudia propiedades como la convergencia de secuencias de números reales, los límites de funciones, el cálculo con números reales, y la continuidad y suavidad de las funciones.
Ecuaciones Diferenciales
Una ecuación diferencial es una ecuación matemática que relaciona una función desconocida con sus derivadas. Estas ecuaciones son muy importantes en ingeniería, física, economía y biología.
Las ecuaciones diferenciales aparecen cuando se conoce cómo cambian ciertas cantidades en el tiempo o el espacio. Por ejemplo, en la mecánica clásica, el movimiento de un cuerpo se describe con una ecuación diferencial que relaciona su posición, velocidad y las fuerzas que actúan sobre él.
Teoría de la Medida
La teoría de la medida es una forma de asignar un "tamaño" (un número) a partes de un conjunto. Es una generalización de conceptos como la longitud, el área y el volumen. Un ejemplo importante es la medida de Lebesgue, que asigna la longitud, el área y el volumen a subconjuntos del espacio euclidiano.
Técnicamente, una medida es una función que asigna un número no negativo a ciertos subconjuntos de un conjunto. Debe asignar 0 al conjunto vacío y ser aditiva, lo que significa que la medida de un conjunto grande es la suma de las medidas de sus partes más pequeñas.
Análisis Numérico
El análisis numérico es el estudio de algoritmos que usan aproximaciones para resolver problemas del análisis matemático. A diferencia de las soluciones exactas, el análisis numérico busca soluciones aproximadas, pero manteniendo un control sobre los posibles errores.
El análisis numérico se aplica en muchos campos, como la ingeniería y las ciencias físicas. En el siglo XXI, también se usa en ciencias de la vida y otras áreas. Por ejemplo, las ecuaciones diferenciales ordinarias se usan en la mecánica celeste para estudiar planetas y estrellas.
Subdivisiones del Análisis Matemático
El análisis matemático es un campo muy amplio que incluye varias ramas:
- Análisis real: El estudio riguroso de las derivadas e integrales de funciones con valores reales, incluyendo límites y series.
- Ecuaciones diferenciales ordinarias y en derivadas parciales.
- Geometría diferencial: Extiende los métodos del análisis real a espacios más generales.
- Integración y teoría de la medida: Generaliza el concepto de cálculo integral.
- Teoría de la probabilidad: Comparte formalismo con la teoría de la medida.
- Análisis numérico: Diseña algoritmos para simular procesos matemáticos complejos.
- Análisis no estándar: Investiga ciertos números hiperreales y sus funciones.
- Análisis no real: Extiende el análisis real a otros tipos de números.
- Análisis complejo: Estudia funciones que van del plano complejo a sí mismo.
- Análisis p-ádico: El análisis en el contexto de los números p-ádicos.
- Análisis funcional: Estudia espacios y funciones, introduciendo conceptos como los espacios de Banach y espacios de Hilbert.
- Análisis armónico: Trata sobre las series de Fourier.
- Geometría analítica: Relaciona puntos y conjuntos con coordenadas.
- Topología
- Topología diferencial: Generaliza el análisis real y complejo a espacios topológicos más generales.
- Topología algebraica
- Grupos de Lie
- Otras áreas:
Galería de imágenes
-
El estudio del conjunto de Mandelbrot, que es un objeto fractal, involucra diversas áreas del análisis matemático.
-
Conjuntos Numéricos
Véase también
En inglés: Mathematical analysis Facts for Kids
