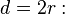Área para niños
El área es una medida que nos dice qué tan grande es una superficie o una figura plana. Imagina que quieres saber cuánto espacio ocupa una alfombra en el suelo; esa medida sería su área. Se expresa en unidades de medida especiales llamadas unidades de superficie, como los metros cuadrados.
El área es una magnitud que nos ayuda a entender la extensión de algo en dos dimensiones. Por ejemplo, el área de una hoja de papel o de un campo de fútbol.
Para figuras planas con lados rectos, como los polígonos, es más fácil entender el área. Podemos dividir cualquier polígono en triángulos y sumar el área de cada uno. A veces, la palabra "área" se usa como sinónimo de "superficie", pero el área es la medida de esa superficie.
Cuando hablamos de objetos con superficies curvas, como una esfera (una pelota), un cono o un cilindro, el área de su parte exterior se llama área superficial. Los antiguos griegos ya sabían cómo calcular el área de las superficies de formas sencillas. Para figuras más complejas, se usan métodos matemáticos avanzados.
Contenido
¿Cómo se descubrió el concepto de área?
La idea de medir el tamaño de una región dentro de una figura geométrica es muy antigua. En el antiguo Egipto, el río Nilo se desbordaba cada año e inundaba los campos. Después, necesitaban calcular el área de cada parcela para saber dónde estaban los límites. Para resolver esto, los egipcios inventaron la geometría, según el historiador Heródoto.
El método de calcular el área de un polígono sumando las áreas de triángulos fue propuesto por primera vez por el sabio griego Antifón alrededor del año 430 a.C. Calcular el área de una figura curva era más difícil. El método exhaustivo consistía en dibujar polígonos dentro y fuera de la figura, aumentando el número de lados de esos polígonos para acercarse cada vez más al área real. Con este método, Eudoxo logró una buena aproximación para el área de un círculo. Más tarde, Arquímedes usó este sistema para resolver problemas similares y para calcular el valor aproximado del número π.
¿Cómo se calcula el área de un círculo?
En el siglo V a.C., Hipócrates de Quíos fue el primero en demostrar que el área de un círculo es proporcional al cuadrado de su diámetro. Esto significa que si el diámetro se duplica, el área se multiplica por cuatro. Eudoxo de Cnido, también en el siglo V a.C., descubrió que el área de un círculo es proporcional al cuadrado de su radio.
El matemático Arquímedes usó la geometría euclidiana para demostrar que el área de un círculo es igual a la de un triángulo rectángulo cuya base tiene la misma longitud que la circunferencia del círculo y cuya altura es igual al radio del círculo. La circunferencia es 2πr, y el área de un triángulo es la mitad de la base por la altura, lo que nos da la famosa fórmula del área del círculo: πr2. Arquímedes aproximó el valor de π dibujando polígonos regulares dentro y fuera de un círculo, aumentando el número de lados para que el área del polígono se acercara cada vez más a la del círculo.
En 1761, el científico suizo Johann Heinrich Lambert demostró que π es un número irracional, lo que significa que no se puede escribir como una fracción simple. En 1794, el matemático francés Adrien-Marie Legendre demostró que π2 también es irracional. Finalmente, en 1882, el matemático alemán Ferdinand von Lindemann demostró que π es un número trascendental, lo que significa que no es la solución de ninguna ecuación polinómica con números enteros.
¿Cómo se calcula el área de un triángulo?
Herón de Alejandría encontró lo que se conoce como la fórmula de Herón para calcular el área de un triángulo si conoces la longitud de sus tres lados. Esta fórmula se encuentra en su libro Métrica, escrito alrededor del año 60 d.C. Se cree que Arquímedes ya conocía esta fórmula mucho antes.
En el año 499, Aryabhata, un matemático y astrónomo de la India, expresó el área de un triángulo como la mitad de la base por la altura en su libro Aryabhatiya.
Los chinos también descubrieron una fórmula similar a la de Herón de forma independiente. Fue publicada en 1247 en el libro Shushu Jiuzhang ("Tratado matemático en nueve secciones"), escrito por Qin Jiushao.
¿Qué es la confusión entre área y perímetro?
El perímetro es la medida del contorno de una figura, mientras que el área es la medida de su superficie. Aunque son diferentes, a veces se confunden. Si agrandamos o reducimos una figura, tanto su área como su perímetro cambian. Por ejemplo, si un terreno se muestra en un mapa a escala 1:10 000, el perímetro real se calcula multiplicando el perímetro del mapa por 10 000, y el área real se calcula multiplicando el área del mapa por 10 0002.
Sin embargo, no hay una relación directa entre el área y el perímetro de cualquier figura. Por ejemplo, un rectángulo con un área de un metro cuadrado puede tener diferentes perímetros. Podría medir 0.5 metros de largo por 2 metros de ancho (perímetro de 5 metros), o 0.001 metros de largo por 1000 metros de ancho (perímetro de más de 2000 metros). El filósofo Proclo (siglo V d.C.) cuenta que los campesinos griegos a veces dividían sus campos "equitativamente" según el perímetro, pero esto resultaba en áreas diferentes. La producción de un campo depende de su área, no de su perímetro.
Fórmulas para calcular el área
Fórmulas de polígonos
Para un polígono simple (que no se cruza a sí mismo) cuyos coordenadas de sus vértices 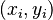 se conocen, el área se puede calcular con la fórmula del área de Gauss:
se conocen, el área se puede calcular con la fórmula del área de Gauss:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{1}{2} \Biggl\vert \sum_{i = 0}^{n - 1}( x_i y_{i + 1} - x_{i + 1} y_i) \Biggr\vert
Rectángulos y cuadrados
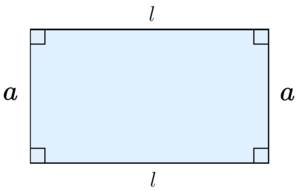
La fórmula más sencilla para el área es la de un rectángulo. Si un rectángulo tiene un largo 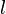 y un ancho
y un ancho  , su área es:
, su área es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A=l\times a (rectángulo).
Para un cuadrado, como todos sus lados son iguales (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): l = a = c ), la fórmula del área es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A=c^2 (cuadrado).
Paralelogramos y triángulos
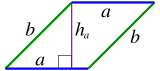
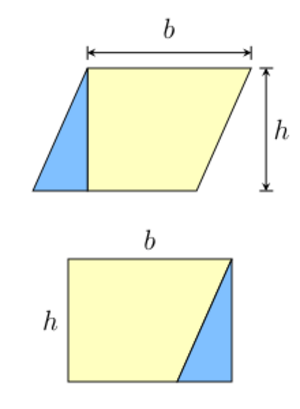
Muchas fórmulas de área se basan en la idea de "cortar y pegar" figuras. Por ejemplo, un paralelogramo (una figura de cuatro lados con lados opuestos paralelos) se puede transformar en un rectángulo. Si cortas un triángulo de un lado y lo mueves al otro, obtienes un rectángulo. Por lo tanto, el área de un paralelogramo es igual a la de un rectángulo:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A=b\times h (paralelogramo).
Donde  es la base y
es la base y  es la altura.
es la altura.
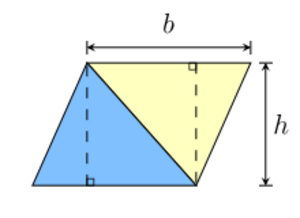
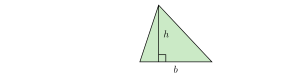
Un paralelogramo también se puede dividir en dos triángulos iguales cortándolo por una diagonal. Esto significa que el área de cada triángulo es la mitad del área del paralelogramo:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{1}{2}bh (triángulo).
Se pueden usar ideas similares para encontrar las fórmulas de área de otras figuras como el trapecio.
Área de las formas curvas
Círculos
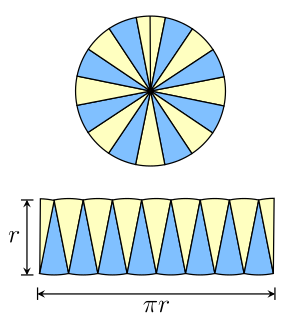
La fórmula del área de un círculo (o más precisamente, el área de un disco) se basa en un método similar. Si divides un círculo de radio  en muchos sectores pequeños, cada sector parece un triángulo. Puedes reorganizar estos sectores para formar una figura que se parece mucho a un paralelogramo. La altura de este "paralelogramo" es
en muchos sectores pequeños, cada sector parece un triángulo. Puedes reorganizar estos sectores para formar una figura que se parece mucho a un paralelogramo. La altura de este "paralelogramo" es  , y su ancho es la mitad de la circunferencia del círculo, que es
, y su ancho es la mitad de la circunferencia del círculo, que es 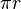 . Así, el área total del círculo es:
. Así, el área total del círculo es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A=\pi r^2 (círculo).
Cuantos más sectores dividas el círculo, más precisa será esta aproximación. El cálculo nos permite demostrar que el límite de las áreas de estos paralelogramos aproximados es exactamente 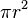 .
.
Elipses

La fórmula del área de una elipse (una forma ovalada) está relacionada con la del círculo. Para una elipse con semiejes  e
e  (que son como los radios en un círculo, pero en dos direcciones diferentes), la fórmula es:
(que son como los radios en un círculo, pero en dos direcciones diferentes), la fórmula es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A= \pi xy
Área superficial
Las fórmulas básicas para el área superficial (el área de la "piel" de un objeto tridimensional) se pueden obtener a menudo "desplegando" la superficie. Por ejemplo, si cortas la superficie lateral de un cilindro a lo largo, puedes aplanarla para formar un rectángulo. De manera similar, la superficie lateral de un cono se puede aplanar para formar un sector de un círculo.
La fórmula para el área superficial de una esfera es más compleja porque no se puede aplanar sin deformarse. Arquímedes fue el primero en encontrar esta fórmula en su obra Sobre la esfera y el cilindro. La fórmula es:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A=4\pi r^2 (esfera).
Donde  es el radio de la esfera.
es el radio de la esfera.
Fórmulas generales
Áreas de figuras bidimensionales
- Un triángulo:
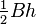 (donde
(donde  es la base y
es la base y 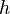 es la altura). Si conoces los tres lados (
es la altura). Si conoces los tres lados ( ,
,  ,
,  ), puedes usar la fórmula de Herón:
), puedes usar la fórmula de Herón: 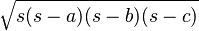 , donde
, donde 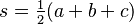 es el semiperímetro.
es el semiperímetro. - Un polígono simple en una cuadrícula de puntos (con vértices en los puntos de la cuadrícula): el área es
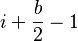 , donde
, donde  es el número de puntos de la cuadrícula dentro del polígono y
es el número de puntos de la cuadrícula dentro del polígono y  es el número de puntos en el borde. Esto se conoce como teorema de Pick.
es el número de puntos en el borde. Esto se conoce como teorema de Pick.
Área en el cálculo
El cálculo es una herramienta matemática poderosa para encontrar áreas, especialmente de formas irregulares o bajo curvas.
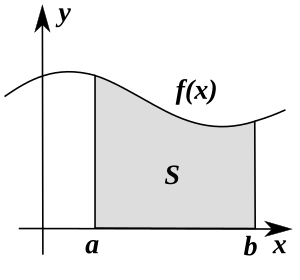
- El área bajo una curva (una línea que representa una función matemática) y el eje horizontal, entre dos puntos
 y
y  , se calcula con una integral definida:
, se calcula con una integral definida:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \int_a^{b} f(x) \, dx
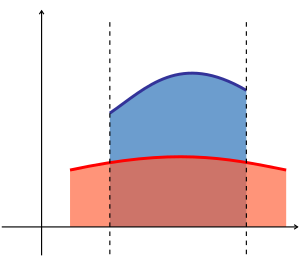
- El área entre las gráficas de dos funciones,
 y
y 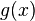 , se calcula restando sus integrales:
, se calcula restando sus integrales:
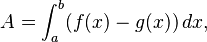 donde
donde  es la función que está por encima de la otra.
es la función que está por encima de la otra.
Área superficial de las figuras tridimensionales
- Cono:
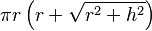 , donde
, donde  es el radio de la base y
es el radio de la base y 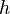 es la altura. También se puede escribir como
es la altura. También se puede escribir como  , donde
, donde 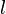 es la altura inclinada del cono.
es la altura inclinada del cono. - cubo:
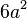 , donde
, donde  es la longitud de una arista.
es la longitud de una arista. - cilindro:
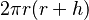 , donde
, donde  es el radio de la base y
es el radio de la base y 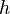 es la altura.
es la altura. - prisma:
 , donde
, donde  es el área de una base,
es el área de una base,  es el perímetro de una base y
es el perímetro de una base y 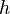 es la altura.
es la altura. - pirámide:
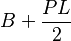 , donde
, donde  es el área de la base,
es el área de la base,  es el perímetro de la base y
es el perímetro de la base y 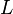 es la longitud de la inclinación.
es la longitud de la inclinación. - prisma rectangular:
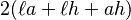 , donde
, donde 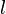 es la longitud,
es la longitud,  es la anchura y
es la anchura y 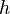 es la altura.
es la altura.
Relación área-perímetro
Para una figura cerrada en un plano, existe una relación entre su área ( ) y su perímetro (
) y su perímetro (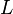 ):
):
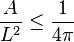
Esta relación nos dice que, para un perímetro dado, el círculo es la figura que encierra la mayor área. La igualdad solo se cumple para un círculo; para cualquier otra forma, el área será menor en proporción a su perímetro.
Lista de fórmulas comunes
| Forma | Fórmula | Variables |
|---|---|---|
| Rectángulo |  |
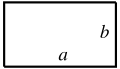 |
| Triángulo rectángulo | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A = \frac{ab}{2} | 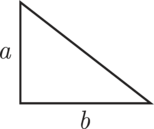 |
| Triángulo | 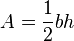 |
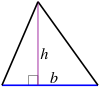 |
| Triángulo | 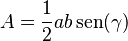 |
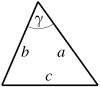 |
| Triángulo (fórmula de Herón) |
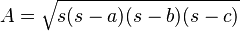 |
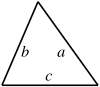 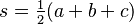 |
| Triángulo isósceles | 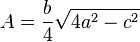 |
 |
| Triángulo equilátero | 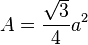 |
 |
| Rombo/deltoide | 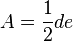 |
 |
| Paralelogramo | 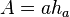 |
 |
| Trapecio | 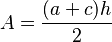 |
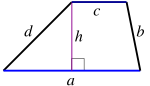 |
| Hexágono regular | 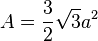 |
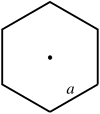 |
| Octágono regular | 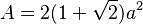 |
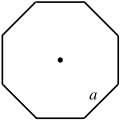 |
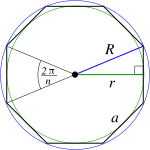
| Polígono regular (de lados |
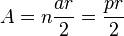
|
|
| Círculo | 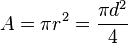 ( |
 |
| Sector circular | 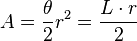 |
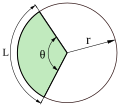 |
| Elipse |  |
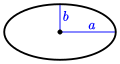 |
| Integral |  |
 |
| Área superficial | ||
| Esfera | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p = 4\pi r^2 = \pi d^2 |  |
| Ortoedro | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p = 2(ab+ac+bc) |  |
| Cilindro
(incl. parte inferior y superior) |
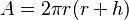 |
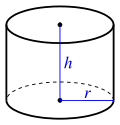 |
| Cono
(incl. la parte inferior) |
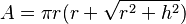 |
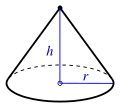 |
| Toro | 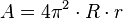 |
 |
| Superficie de revolución | ![A = 2\pi\int_a^b\! f(x)\sqrt{1+\left[f'(x)\right]^2}\mathrm{d}x](/images/math/2/5/b/25b1a2b0f94ced89af350e08a5e5254a.png) (rotación alrededor del eje x) |
 |
Estas fórmulas nos ayudan a encontrar las áreas de muchas formas comunes. Las áreas de polígonos irregulares se pueden calcular con la fórmula de la lazada.
Unidades de medida de superficies

Las unidades de superficie son medidas estándar que usamos para comparar y comunicar el tamaño de una superficie, área o extensión de un objeto, terreno o figura geométrica.
Medir es la técnica de asignar un número a una propiedad física, comparándola con un patrón que tomamos como unidad. Si usamos diferentes unidades, la medida de una superficie dará resultados distintos. Por eso, es importante tener unidades de medida únicas para que la información sea fácil de entender.
Sistema Internacional de Unidades
El Sistema Internacional de Unidades (SI) tiene sus propias unidades para medir el área:
- Múltiplos (unidades más grandes)
- Kilómetro cuadrado (km²): 1 000 000 metros cuadrados.
- Hectómetro cuadrado (hm²) o hectárea (ha): 10 000 metros cuadrados.
- Decámetro cuadrado (dam²) o área (a): 100 metros cuadrados.
- Unidad básica
- metro cuadrado (m²): Es la unidad principal del SI para el área.
- Submúltiplos (unidades más pequeñas)
- Decímetro cuadrado (dm²): 0.01 m² (una centésima de metro cuadrado).
- Centímetro cuadrado (cm²): 0.0001 m² (una diezmilésima de metro cuadrado).
- Milímetro cuadrado (mm²): 0.000001 m² (una millonésima de metro cuadrado).
- barn: 10−28 m². Esta unidad se usa en física nuclear para describir el área de interacción de partículas muy pequeñas.
Sistema anglosajón de unidades
En el Sistema anglosajón de unidades, algunas unidades comunes para el área son:
- pulgada cuadrada
- pie cuadrado
- yarda cuadrada
- El acre se usa mucho para medir terrenos. Un acre equivale a 4840 yardas cuadradas o 43 560 pies cuadrados.
Véase también
 En inglés: Area Facts for Kids
En inglés: Area Facts for Kids
- Unidad de medida
- Metrología
- Áreas de figuras geométricas




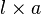 .
.
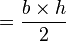
 )
)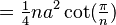
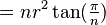
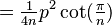
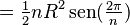
 (
(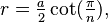
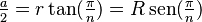
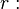 radio de la circunferencia inscrita
radio de la circunferencia inscrita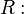 radio de la circunferencia circunscrita
radio de la circunferencia circunscrita