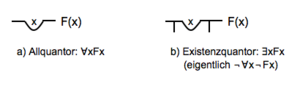Gottlob Frege para niños
Datos para niños Gottlob Frege |
||
|---|---|---|
 Gottlob Frege cerca de 1879.
|
||
| Información personal | ||
| Nombre de nacimiento | Friedrich Ludwig Gottlob Frege | |
| Nacimiento | 8 de noviembre de 1848 Wismar (Mecklemburgo-Schwerin, Confederación Germánica) |
|
| Fallecimiento | 26 de julio de 1925 Bad Kleinen (Estado Libre de Mecklemburgo-Schwerin, República de Weimar) |
|
| Sepultura | Cementerio de Wismar | |
| Nacionalidad | Alemana | |
| Familia | ||
| Cónyuge | Margarete Katharina Sophia Anna Lieseberg | |
| Educación | ||
| Educación | doctor en Filosofía y habilitación universitaria | |
| Educado en |
|
|
| Supervisor doctoral | Ernst Christian Julius Schering y Alfred Clebsch | |
| Alumno de | ||
| Información profesional | ||
| Ocupación | Lógico, filósofo analítico, filósofo del lenguaje, profesor universitario y matemático | |
| Área | Filosofía | |
| Empleador | Universidad de Jena | |
| Obras notables | Begriffsschrift Los fundamentos de la aritmética Sobre el sentido y la referencia |
|
| Miembro de | Academia Alemana de las Ciencias Naturales Leopoldina (desde 1895) | |
Friedrich Ludwig Gottlob Frege (nacido en Wismar, el 8 de noviembre de 1848, y fallecido en Bad Kleinen, el 26 de julio de 1925) fue un matemático, lógico y filósofo alemán. Se le considera una figura muy importante en el desarrollo de la lógica matemática y de la filosofía analítica. Se interesó mucho por cómo funciona el lenguaje y las matemáticas.
Frege trabajó como profesor de matemáticas en la Universidad de Jena. Durante mucho tiempo, sus ideas no fueron muy conocidas. Sin embargo, gracias a otros pensadores como Giuseppe Peano y Bertrand Russell, su trabajo se difundió y fue reconocido por futuras generaciones de filósofos y matemáticos.
Frege creía que las matemáticas y el lenguaje podían entenderse mejor si se basaban en la lógica. Para demostrarlo, investigó a fondo los principios lógicos de ambos campos. Así, ayudó a crear la lógica matemática moderna y los primeros estudios importantes en filosofía del lenguaje. Su forma de pensar, clara y rigurosa, y su influencia en filósofos como Bertrand Russell y Ludwig Wittgenstein, fueron clave para el nacimiento de la filosofía analítica.
Entre sus obras más importantes se encuentran Begriffsschrift (1879), que sentó las bases de la lógica moderna, y Grundlagen der Arithmetik (1884), donde explicó los principios filosóficos de las matemáticas. Su artículo Über Sinn und Bedeutung (1892) es fundamental para la filosofía del lenguaje.
Contenido
Biografía de Gottlob Frege
Primeros años y estudios
Gottlob Frege nació en 1848 en Wismar, una ciudad que entonces formaba parte del Gran Ducado de Mecklemburgo-Schwerin, en la actual Alemania. Su padre, Carl Alexander Frege, fue cofundador y director de una escuela para niñas. Cuando su padre falleció en 1866, su madre, Auguste Wilhelmine Sophie Frege, tomó la dirección de la escuela.
Desde pequeño, Frege estuvo en contacto con ideas que influirían en su carrera. Por ejemplo, su padre escribió un libro de texto sobre el idioma alemán que incluía una sección sobre la estructura lógica del lenguaje.
Frege estudió en el gymnasium de Wismar y se graduó en 1869. Su profesor de literatura, Gustav Adolf Leo Sachse, lo animó a seguir estudiando ciencias naturales en la Universidad de Jena.
En 1869, Frege se matriculó en matemáticas en la Universidad de Jena. Allí estudió durante dos años, tomando unas 20 asignaturas, principalmente de matemáticas y física, pero también de filosofía kantiana. Su profesor más influyente fue el físico Ernst Karl Abbe, con quien mantuvo una amistad cercana. Abbe fue su mentor durante toda su carrera.
Ernst Abbe era una figura muy importante en Jena. Ayudó a la familia Zeiss a fundar la empresa de productos ópticos Carl Zeiss AG. Como director técnico, transformó la empresa en una de las más grandes de Alemania. Abbe también dirigía la fundación Carl Zeiss, que usaba parte de las ganancias de la empresa para apoyar la investigación científica. Frege se benefició mucho de esta fundación gracias a Abbe.
En 1871, después de graduarse en Jena, Frege continuó sus estudios en la Universidad de Gotinga, que en ese momento era muy reconocida en matemáticas. Estudió con varios profesores importantes, incluyendo a Alfred Clebsch y Ernst Christian Julius Schering.
En 1873, Frege obtuvo su doctorado bajo la supervisión de Ernst Schering. Su tesis se tituló "Sobre una representación geométrica de formas imaginarias en el plano". En ella, buscaba resolver problemas sobre cómo representar puntos imaginarios en la geometría.
Carrera en Jena: Primeros trabajos (1874-1893)
En mayo de 1874, Frege regresó a Jena. Había completado su Habilitationsschrift (un trabajo para obtener el derecho a enseñar en la universidad) sobre la teoría de los números complejos. Gracias a Abbe, consiguió un puesto de privatdozent, que era el primer paso en la carrera académica en Alemania, aunque no era remunerado al principio.
Ideografía (1879)
Al principio, Frege enseñó matemáticas y sus primeros trabajos fueron en análisis complejo y geometría. No se sabe con exactitud qué lo llevó a interesarse por la filosofía de las matemáticas. Parece que su interés por los fundamentos lógicos de las matemáticas surgió temprano. Al estudiar la justificación de los números enteros, se dio cuenta de que las matemáticas de su tiempo no ofrecían una explicación formal suficiente. Esto lo llevó a desarrollar un nuevo tipo de lógica.
Frege llegó a la conclusión de que la aritmética podía basarse en la lógica formal. Creía que nuestra comprensión de los números naturales no venía de la experiencia directa, sino del lenguaje y de nuestra capacidad de razonar lógicamente. Esta idea se conoce como logicismo.
En 1879, Frege publicó su primera gran obra, la Ideografía (Begriffsschrift). En este libro, la "Ideografía" se refiere a un sistema de símbolos y reglas que Frege creó para aclarar las relaciones lógicas en el lenguaje. Desde Aristóteles, la lógica se había basado en el cálculo proposicional, que usa operadores lógicos como "no", "y", "o" para determinar la verdad de las oraciones.
La Ideografía de Frege fue el primer estudio sistemático de la lógica proposicional. Su mayor aporte fue la invención de la teoría de la cuantificación. Con ella, Frege pudo analizar la validez lógica de expresiones que incluyen palabras como "todo", "nada", "algunos" o "cualquiera". Esto fue un gran avance en la historia de la lógica formal, el más importante desde Aristóteles.
Sin embargo, la notación que Frege usó en su Ideografía era muy compleja y difícil de imprimir. Era tabular y bidimensional, lo que no gustó a editores ni a lectores. Además, Frege no separó bien su notación de la semántica (el significado) y la sintaxis (la estructura) que representaba. Por eso, muchas de sus ideas importantes fueron ignoradas.
La Ideografía fue recibida con mucha crítica, principalmente por su difícil notación. Frege también ignoró los trabajos recientes de otros lógicos, lo que contribuyó a que su obra no fuera comprendida. A pesar de la mala recepción, la Ideografía le ayudó a conseguir un puesto de profesor en Jena, que mantuvo hasta su jubilación.
Fundamentos de la Aritmética (1884)
Para evitar las críticas a su notación, Frege escribió su siguiente obra importante, Grundlagen der Arithmetik ("Fundamentos de la Aritmética"), en un estilo diferente, sin usar símbolos complejos. En este libro, Frege propuso que la aritmética se puede derivar de la lógica.
Aunque el Grundlagen es una de las obras más importantes de Frege, su recepción fue aún más fría que la de la Ideografía. Solo recibió tres reseñas, y todas fueron negativas. Se cree que, al no usar símbolos, el contenido pudo ser demasiado técnico para los filósofos y demasiado filosófico para los matemáticos.
A pesar de la falta de comprensión, el Grundlagen presentó dos ideas muy novedosas: primero, que cada número es un objeto que existe por sí mismo; y segundo, que asignar un número a una oración es una afirmación sobre un concepto. Esto significaba que los números no eran solo una propiedad de las cosas o algo subjetivo. Así, Frege separó la lógica de la psicología y la epistemología (el estudio del conocimiento).
En 1887, Frege se casó con Margarete Katharina Sophia Anna Liesebe. Tuvieron dos hijos que fallecieron en la infancia, y luego adoptaron a un niño, Alfred Frege.
La década siguiente a la publicación del Grundlagen fue muy productiva para Frege. Se centró en la filosofía del lenguaje. Publicó tres artículos en 1891 y 1892 que cambiaron este campo para siempre. El más importante fue Über Sinn und Bedeutung ("Sobre el sentido y la referencia"). En este artículo, Frege explicó la diferencia entre el sentido de una expresión (cómo se presenta un objeto) y su referencia (el objeto mismo).
Última etapa y legado (1893-1925)
La última gran obra de Frege fue Grundgesetze der Arithmetik ("Leyes Básicas de la Aritmética"), cuyo primer volumen apareció en 1893. En este libro, Frege intentó construir la aritmética formalmente a partir de la lógica. Quería demostrar que las matemáticas podían reducirse a la lógica. Sin embargo, tuvo dos grandes problemas. Primero, ningún editor quería publicar la obra debido a los fracasos anteriores. Finalmente, un editor de Jena aceptó, pero solo en dos volúmenes y el segundo solo si el primero tenía éxito.
El primer volumen del Grundgesetze también fue recibido con poco entusiasmo, lo que retrasó la publicación del segundo volumen por una década. A pesar de esto, su publicación le valió a Frege un ascenso a una cátedra honorífica en Jena, con un buen salario de la fundación Carl Zeiss, gracias a su amigo Ernst Abbe.
Aunque no fue un éxito de ventas, el Grundgesetze atrajo la atención de la comunidad internacional. Su publicación generó una discusión con el matemático italiano Giuseppe Peano, quien tuvo que modificar sus propias ideas sobre la aritmética para incluir las críticas de Frege. Esta discusión con Peano llamó la atención de Bertrand Russell, un joven filósofo de la Universidad de Cambridge.
Entre 1893 y 1903, Frege escribió artículos criticando a otros filósofos y matemáticos. Por ejemplo, criticó la obra de Edmund Husserl, quien aceptó las críticas de Frege y cambió su forma de pensar sobre las matemáticas.
El segundo gran problema del Grundgesetze apareció en 1902, cuando el segundo volumen ya estaba en imprenta. Frege recibió una carta de Bertrand Russell. Russell le señalaba que el quinto principio básico del Grundgesetze hacía que todo el sistema fuera inconsistente. Esta inconsistencia se conoce como la paradoja de Russell.
Frege se sorprendió mucho con la carta de Russell. A diferencia de otros, Frege reconoció el problema y trató de modificar el quinto principio en un apéndice del segundo volumen del Grundgesetze. Su solución no fue del todo consistente, pero Frege siguió defendiéndola por un tiempo.
Antes de jubilarse en 1918, Frege aceptó que su sistema logicista había fallado en ese punto. Para entonces, la lógica matemática que él había iniciado ya era muy importante, aunque Frege seguía siendo poco reconocido. Dedicó el resto de su vida a estudiar la relación entre la lógica y la psicología. Murió en 1925 en Bad Kleinen, dejando sus escritos a su hijo adoptivo Alfred.
Diario personal
Frege era una persona reservada. Sus alumnos decían que daba clase mirando a la pizarra y que a veces hacía comentarios sarcásticos. Sus opiniones personales se conocen principalmente a través de su diario privado, descubierto en los años 70.
Ideas principales de Gottlob Frege
En 1879, Frege publicó su obra Ideografía o Escritura de conceptos (Begriffsschrift). En ella, estableció las bases de la lógica matemática moderna, un campo que había cambiado poco desde Aristóteles. Introdujo una nueva forma de escribir la lógica, incluyendo los cuantificadores ("para todo" o "para al menos uno"), lo que permitió analizar muchos más tipos de argumentos. También fue el primero en diferenciar las reglas formales de la lógica de su significado.
Una vez que estableció los principios de la lógica, se propuso construir la aritmética basándose en ellos. La notación de Frege era muy extensa. No fue hasta la publicación de los Principia mathematica de Alfred North Whitehead y Bertrand Russell que el poder de la lógica formal se hizo más evidente, usando una notación más compacta.
Logicismo: Matemáticas y Lógica
Frege fue un defensor del logicismo. Esta idea sostiene que las matemáticas pueden reducirse a la lógica. Es decir, las verdades matemáticas pueden deducirse de las verdades lógicas. Sin embargo, Frege aplicó esta idea principalmente a la aritmética y a la teoría de conjuntos, ya que mantenía una visión más tradicional sobre la geometría. Su obra Leyes básicas de la aritmética (Grundgesetze der Arithmetik) fue un intento de llevar a cabo este proyecto logicista.
En 1902, mientras se imprimía el segundo volumen de su obra, recibió la famosa carta de Bertrand Russell. Russell le advirtió sobre una grave inconsistencia en su sistema lógico, conocida como la paradoja de Russell.
Frege añadió rápidamente una modificación a uno de sus axiomas en un apéndice de la obra para intentar solucionar el problema. Este descubrimiento afectó mucho su trabajo académico. A pesar de la indiferencia de sus contemporáneos, y tras la muerte de su esposa, se retiró. Fue Bertrand Russell quien, al llegar a conclusiones similares de forma independiente, reconoció el gran valor de la obra de Frege y la dio a conocer. Aunque la paradoja de Russell arruinó el proyecto logicista de Frege, él siguió trabajando y publicó artículos importantes, como El pensamiento: una investigación lógica, donde examinó el contenido objetivo de las oraciones. En los años sesenta, el filósofo Michael Dummett publicó libros importantes sobre Frege, lo que revivió el interés por su trabajo.
Filosofía del lenguaje: Sentido y Referencia
La teoría del significado de Frege se opuso a la idea de que las palabras solo representan ideas mentales. En su artículo Sobre el sentido y la referencia, Frege inició una importante corriente en la filosofía del lenguaje.
Tradicionalmente, se pensaba que las palabras eran signos de "ideas internas" en nuestra mente, como lo propuso John Locke. Según esta visión, el lenguaje era una herramienta para comunicar esas ideas subjetivas.
Frege, sin embargo, analizó las oraciones de identidad, como "a = a" y "a = b". Se preguntó por qué "a = a" es obvio, pero "a = b" puede darnos nueva información. Para resolver esto, distinguió entre la referencia y el sentido de una expresión. La referencia es el objeto al que se refiere un signo, y el sentido es la forma en que ese objeto se nos presenta. Por ejemplo, en "Venus es Héspero", ambas palabras se refieren al mismo planeta, pero "Venus" y "Héspero" son dos formas diferentes de hablar de él, con distintos sentidos.
Frege rechazó la idea de que las palabras solo significan ideas privadas en la mente de las personas. En cambio, defendió un realismo del significado. Para él, nuestras palabras se refieren a objetos del mundo y también expresan cómo se nos presentan esos objetos (su sentido). El sentido no es una representación subjetiva. Frege dijo que "la humanidad tiene un tesoro común de pensamientos, que transmite de una generación a otra". Esto significa que los sentidos o significados de las palabras pertenecen a comunidades de hablantes, no solo a la mente de un individuo. Lo que es exclusivo de cada persona son sus representaciones subjetivas.
Frege también señaló que no todas las expresiones se refieren a un objeto real. Por ejemplo, "el mayor número natural" o "el político más inútil" no tienen una referencia única, porque siempre hay uno mayor o más inútil. Sin embargo, el significado de estas expresiones tampoco son ideas privadas.
Influencia de Gottlob Frege
El trabajo de Frege en los fundamentos de las matemáticas influyó directamente en los Principia Mathematica de Bertrand Russell y Alfred North Whitehead. Filósofos como Ludwig Wittgenstein y Edmund Husserl también fueron muy influenciados por Frege. Rudolf Carnap adoptó muchas de las ideas logicistas de Frege y desarrolló gran parte de su filosofía basándose en él. Por todo esto, Frege es considerado el padre de la escuela analítica de filosofía.
Frege fue una figura clave para la filosofía del lenguaje. La distinción entre sentido y referencia, y entre concepto y objeto, se deben a él. En 1930, los teoremas de incompletitud de Gödel mostraron que el proyecto logicista de Frege tenía limitaciones. Estos teoremas demuestran que en cualquier sistema formal lo suficientemente potente para expresar la aritmética, siempre habrá afirmaciones verdaderas que no se pueden demostrar ni refutar dentro de ese sistema. A pesar de esto, la contribución de Frege como pionero de la lógica matemática es ampliamente reconocida.
Obras destacadas
- Ideografía (1879) (Begriffsschrift)
- Los fundamentos de la aritmética (1884) (Die Grundlagen der Arithmetik)
- Las leyes básicas de la aritmética (dos volúmenes) (1893-1903) (Grundgesetze der Arithmetik)
- Sobre el sentido y la referencia (1892) (Über Sinn und Bedeutung)
Galería de imágenes
-
Busto de bronce del matemático, lógico y filósofo alemán Gottlob Frege por Karl Heinz Appelt en Wismar.
Véase también
 En inglés: Gottlob Frege Facts for Kids
En inglés: Gottlob Frege Facts for Kids
- Logicismo
- Cálculo proposicional de Frege
- Teorema de Frege
- Filosofía analítica