Álgebra de Boole para niños
El álgebra de Boole, también conocida como álgebra booleana, es una parte de las matemáticas que nos ayuda a entender cómo funcionan las operaciones lógicas. Es muy importante en la electrónica digital y la informática.
Fue creada por George Boole en 1847. Él la explicó en su libro The Mathematical Analysis of Logic. Más tarde, en 1854, la detalló en An Investigation of the Laws of Thought.
El álgebra de Boole es clave para el desarrollo de los aparatos electrónicos que usamos hoy. También se usa en todos los lenguajes de programación modernos. Además, es útil en la teoría de conjuntos y en la lógica.
Se diferencia del álgebra que aprendes en la escuela en dos cosas. Primero, en el álgebra de Boole, las variables solo pueden tener dos valores: verdadero (que se representa con un 1) o falso (que se representa con un 0). En el álgebra normal, las variables pueden ser cualquier número. Segundo, el álgebra de Boole usa operaciones lógicas como "y" (llamada conjunción), "o" (llamada disyunción) y "no" (llamada negación). El álgebra normal usa operaciones como sumar, restar, multiplicar y dividir.
Así, el álgebra de Boole es una forma de describir operaciones lógicas, igual que el álgebra normal describe operaciones con números.
Contenido
Historia del Álgebra de Boole
El nombre de esta álgebra es un homenaje a George Boole (1815-1864). Él fue un matemático inglés que aprendió por sí mismo. Fue el primero en definir este sistema lógico. Lo hizo en un pequeño libro en 1847.
El álgebra de Boole buscaba usar técnicas del álgebra para trabajar con expresiones de la lógica proposicional. Esto significa que quería aplicar reglas matemáticas a afirmaciones que pueden ser verdaderas o falsas.
Hoy en día, el álgebra de Boole se usa mucho en el diseño de aparatos electrónicos. Claude Shannon fue el primero en aplicarla a los circuitos eléctricos en 1948. Esta lógica sirve para dos cosas principales:
- Analizar: Ayuda a describir cómo funcionan los circuitos electrónicos.
- Diseñar: Permite crear circuitos a partir de una función lógica que se quiere lograr.
¿Cómo funciona el Álgebra de Boole?
El álgebra de Boole se basa en un conjunto de elementos y algunas reglas para combinarlos. Imagina que solo tienes dos valores: 0 y 1. Estos pueden representar "falso" y "verdadero", o "apagado" y "encendido" en un circuito.
Las operaciones principales son:
- Negación (NO): Cambia un valor a su opuesto. Si es 1, lo convierte en 0. Si es 0, lo convierte en 1.
- Suma lógica (O): Si tienes dos valores, el resultado es 1 si al menos uno de ellos es 1. Solo es 0 si ambos son 0.
- Producto lógico (Y): Si tienes dos valores, el resultado es 1 solo si ambos son 1. Si alguno es 0, el resultado es 0.
Estas operaciones tienen reglas, como las que conoces en el álgebra normal (por ejemplo, el orden en que se hacen las operaciones).
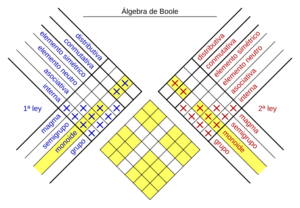
Principios Básicos
El álgebra de Boole tiene una serie de reglas o "axiomas" que siempre se cumplen. Estas reglas son como las leyes de un juego:
- Asociativa: No importa cómo agrupes los valores en una suma o producto, el resultado es el mismo. Por ejemplo, (A Y B) Y C es lo mismo que A Y (B Y C).
- Elemento Neutro: Hay un valor que no cambia el resultado. Para la suma lógica, es el 0 (A O 0 = A). Para el producto lógico, es el 1 (A Y 1 = A).
- Conmutativa: El orden de los valores no cambia el resultado. A O B es lo mismo que B O A.
- Distributiva: Puedes "repartir" una operación sobre otra. Por ejemplo, A Y (B O C) es lo mismo que (A Y B) O (A Y C).
- Complemento: Para cada valor, existe su opuesto. Si sumas un valor con su opuesto, el resultado es 1 (A O NO A = 1). Si los multiplicas, el resultado es 0 (A Y NO A = 0).
Estos principios son la base para resolver problemas y diseñar sistemas lógicos.
Diferentes formas de escribir el Álgebra de Boole
El álgebra de Boole se puede escribir de varias maneras, dependiendo de dónde se use:
- En electrónica digital: Se usan 0 y 1. La negación se escribe con una barra encima (ā), la suma con un más (+) y el producto con un punto (·) o sin nada (AB).
* Ejemplo: NO (A O B) se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \overline {A + B} .
- En lógica: Se usan "F" (falso) y "V" (verdadero). La negación es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lnot , la disyunción (O) es
 y la conjunción (Y) es
y la conjunción (Y) es 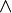 .
.
* Ejemplo: NO (A O B) se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lnot {(A \lor B)} .
- En teoría de conjuntos: Se usan conjuntos. La negación es el complemento (AC), la unión (O) es
 y la intersección (Y) es
y la intersección (Y) es  .
.
* Ejemplo: NO (A O B) se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {(A \cup B)}^C .
Todas estas formas son correctas y se usan en diferentes campos. Lo importante es que la lógica detrás de ellas es la misma.
Aplicaciones del Álgebra de Boole
El álgebra de Boole es muy útil en varios campos:
Lógica Binaria
La lógica binaria es la más conocida del álgebra de Boole. Aquí, solo trabajamos con dos valores: 0 y 1. Estos valores representan el estado de un interruptor (abierto o cerrado) o un bit en una computadora (0 o 1).
- Negación: Si un interruptor está abierto (0), su negación es cerrado (1).
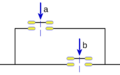
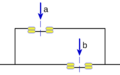
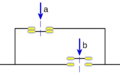
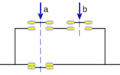
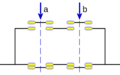
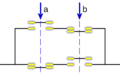
- Suma (O): Imagina dos interruptores en paralelo. La corriente pasa si al menos uno está cerrado.
- Producto (Y): Imagina dos interruptores en serie. La corriente pasa solo si ambos están cerrados.
Estas operaciones son la base de cómo funcionan los circuitos dentro de tu teléfono, computadora o cualquier dispositivo electrónico.
Álgebra de Conjuntos
En la teoría de conjuntos, el álgebra de Boole nos ayuda a entender cómo se relacionan los grupos de cosas.
- El valor "verdadero" se relaciona con el conjunto universal (todo lo que estamos considerando).
- El valor "falso" se relaciona con el conjunto vacío (nada).
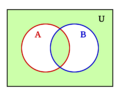
- La operación "NO" es el complemento de un conjunto (todo lo que no está en ese grupo).
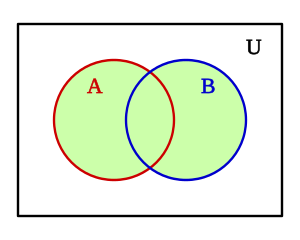
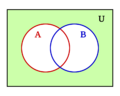
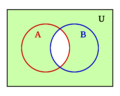
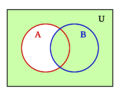
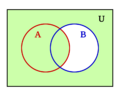
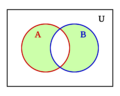
- La operación "O" es la unión de conjuntos (juntar dos grupos).
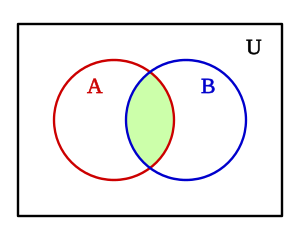
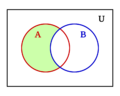
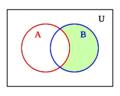
- La operación "Y" es la intersección de conjuntos (lo que tienen en común dos grupos).
Por ejemplo, si tienes un grupo de frutas (U) y un subgrupo de manzanas (A), el complemento de A serían todas las frutas que no son manzanas.
Lógica Proposicional
La lógica proposicional usa el álgebra de Boole para analizar afirmaciones. Una proposición es una frase que puede ser verdadera o falsa, como "Hoy es miércoles" o "El edificio es alto".
- Negación: "NO llueve" es la negación de "Llueve".
- Disyunción (O): "Llueve O hace sol" es verdadera si llueve, si hace sol, o si ambas cosas ocurren.
- Conjunción (Y): "Llueve Y hace frío" es verdadera solo si ambas cosas ocurren al mismo tiempo.
El álgebra de Boole nos permite combinar estas afirmaciones y saber si el resultado es verdadero o falso.
Operaciones Comunes en Álgebra de Boole
Además de las operaciones básicas (NO, O, Y), hay otras operaciones importantes:
- O Exclusiva (XOR): Es verdadera si solo uno de los argumentos es verdadero, pero no ambos. Por ejemplo, "Voy al cine XOR voy al parque" es verdadera si vas a uno, pero no a los dos.
- NO O (NOR): Es verdadera solo si ambos argumentos son falsos. Es lo opuesto a la operación O.
- NO Y (NAND): Es verdadera en todos los casos, excepto cuando ambos argumentos son verdaderos. Es lo opuesto a la operación Y.
Estas operaciones son fundamentales para construir puertas lógicas y circuitos más complejos en la electrónica.
Orden de las Operaciones
Cuando tienes una expresión larga en álgebra de Boole, necesitas saber qué operación hacer primero. Hay una jerarquía, como en las matemáticas normales:
- Negación (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lnot o
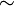 )
) - Conjunción (Y,
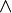 o
o  )
) - Disyunción (O,
 o
o 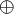 )
) - Implicación (
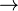 )
) - Bicondicional (
 )
)
Si hay paréntesis, siempre resuelves primero lo que está dentro de ellos, empezando por los más internos. Si tienes varias operaciones con la misma jerarquía, puedes hacerlas de izquierda a derecha o de derecha a izquierda, el resultado será el mismo.
Galería de imágenes
Véase también
 En inglés: Boolean algebra Facts for Kids
En inglés: Boolean algebra Facts for Kids