Combinatoria para niños
La combinatoria es una parte de las matemáticas que nos ayuda a contar y organizar cosas. Imagina que tienes un grupo de objetos y quieres saber de cuántas maneras diferentes puedes agruparlos, ordenarlos o seleccionarlos, siguiendo ciertas reglas. ¡Eso es lo que estudia la combinatoria!
Es muy útil en muchas áreas, como la informática (para entender cómo funcionan los programas), la teoría de probabilidades (para calcular las posibilidades de que algo ocurra) y la física. Aunque al principio muchos problemas de combinatoria se resolvían por separado, con el tiempo se desarrollaron métodos generales que la convirtieron en una rama importante de las matemáticas. Una de sus partes más conocidas es la teoría de grafos, que estudia las conexiones entre puntos.
| Campo | Matemáticas |
|---|---|
| Subcampo | Matemáticas discretas |
| Ramas | Combinatoria enumerativa, Combinatoria analítica, Teoría de la partición, Teoría de grafos, Teoría del diseño, Geometría finita, Teoría del orden, Teoría del matroide, Combinatoria extrema, Combinatoria probabilística, Combinatoria algebraica, Combinatoria de palabras, Combinatoria geométrica, Combinatoria topológica, Combinatoria aritmética, Combinatoria infinita, Combinatoria de conjuntos |
Contenido
Combinatoria: Contando Posibilidades
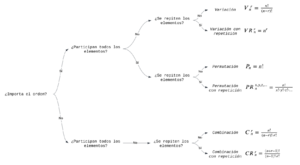
Para resolver un problema de combinatoria, debemos fijarnos en tres cosas clave:
- ¿Importa el orden en que colocamos los elementos?
- ¿Podemos repetir los elementos o deben ser todos diferentes?
- ¿Cuántos elementos tenemos en total y cuántos vamos a elegir?
El diagrama de la derecha te puede ayudar a decidir qué tipo de cálculo usar.
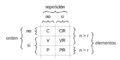
Tipos de Agrupaciones en Combinatoria
La combinatoria se divide en diferentes tipos de agrupaciones, dependiendo de si los elementos se repiten y si el orden importa.
Agrupaciones sin Repetición
Aquí, cada elemento solo puede usarse una vez en cada grupo.
Combinaciones sin Repetición
Las combinaciones son grupos de elementos donde el orden NO importa. Por ejemplo, si eliges a Juan y María para un equipo, es lo mismo que elegir a María y Juan.
La fórmula para calcular las combinaciones de n elementos tomados de r en r es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): C_n^r = \binom{n}{r} = \frac{n!}{r! \cdot (n-r)!} En muchas calculadoras, esto se hace con la tecla nCr.
Ejemplo: En una reunión de 8 personas, se debe formar una comisión de 2 personas. ¿Cuántas comisiones diferentes se pueden formar? Solución: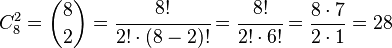 
Se pueden formar 28 comisiones distintas.
Variaciones sin Repetición
Las variaciones son grupos de elementos donde el orden SÍ importa. Por ejemplo, si eliges a Juan como presidente y a María como secretaria, no es lo mismo que María presidenta y Juan secretario.
La fórmula para calcular las variaciones de n elementos tomados de r en r es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V_n^r = \cfrac{n!}{(n-r)!} En muchas calculadoras, esto se hace con la tecla nPr.
Ejemplo: En una carrera con 6 atletas, ¿de cuántas formas distintas podrían repartirse las medallas de oro y plata? Solución: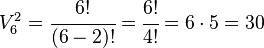 
Hay 30 formas distintas de repartir las medallas.
Permutaciones sin Repetición
Las permutaciones son todas las posibles formas de ordenar un conjunto completo de elementos diferentes. Aquí, el orden SÍ importa y se usan todos los elementos disponibles.
La fórmula para calcular las permutaciones de n elementos es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P_n = n! El símbolo n! se lee "factorial de n" y significa multiplicar n por todos los números enteros positivos menores que él hasta 1 (por ejemplo, 4! = 4 × 3 × 2 × 1 = 24). Por cierto, 0! es igual a 1.
Ejemplo: ¿Cuántos números de 4 cifras distintas pueden escribirse con los dígitos 2, 3, 5 y 8? Solución: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P_4 = 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 Se pueden escribir 24 números distintos.
Agrupaciones con Repetición
En estos casos, algunos elementos pueden aparecer más de una vez en un grupo.
Combinaciones con Repetición
Son grupos de elementos donde el orden NO importa y los elementos SÍ pueden repetirse.
La fórmula para calcular las combinaciones con repetición de n elementos tomados de r en r es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): CR_n^r = \binom{n+r-1}{r} = \cfrac{(n+r-1)!}{r!(n-1)!}
Ejemplo: Un banco ofrece un regalo a elegir entre 5 posibles regalos por cada cartilla. Un señor que tiene tres cartillas, ¿de cuántas formas puede elegir los tres regalos si no le importa repetir? Solución: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): CR_5^3 = \binom{(5+3-1)!}{3!(5-1)!} = \binom{7}{3} = 35 Puede elegir los regalos de 35 formas distintas.
Variaciones con Repetición
Son grupos de elementos donde el orden SÍ importa y los elementos SÍ pueden repetirse.
La fórmula para calcular las variaciones con repetición de n elementos tomados de r en r es: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): VR_n^r = n^r
Ejemplo: ¿Cuántos números distintos de 3 cifras se escriben usando solamente las cifras 1, 2, 5 y 8? Solución: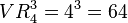 
Se pueden escribir 64 números distintos.
Permutaciones con Repetición
Son las posibles formas de ordenar una secuencia de elementos donde algunos están repetidos.
La fórmula para calcular las permutaciones con repetición es: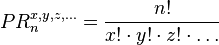 
Donde n es el total de elementos y x, y, z... son las veces que se repite cada elemento.
Ejemplo: ¿Cuántos números distintos de 6 cifras se pueden escribir usando tres unos, dos cincos y un ocho? Solución: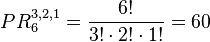 
Se pueden escribir 60 números distintos.
Historia de la Combinatoria
Los primeros conceptos de combinatoria aparecieron hace mucho tiempo. En la antigua India, en el siglo VI a.C., el médico Sushruta ya hablaba de 63 combinaciones posibles a partir de 6 sabores diferentes.
En la Edad Media, matemáticos indios como Mahāvīra (alrededor del año 850) crearon fórmulas para permutaciones y combinaciones. El triángulo aritmético, que muestra las relaciones entre los números de combinaciones, ya se usaba en el siglo X y hoy lo conocemos como el Triángulo de Pascal.
Durante el Renacimiento, la combinatoria volvió a cobrar importancia gracias a trabajos de matemáticos como Pascal, Newton y Euler. En el siglo XX, la combinatoria creció muy rápido, conectándose con otras áreas de las matemáticas y la informática.
¿Para qué sirve la Combinatoria?
La combinatoria tiene muchas aplicaciones prácticas y se relaciona con otras áreas de las matemáticas.
Contar y Organizar: Combinatoria Enumerativa
Esta es la parte más clásica de la combinatoria. Se enfoca en contar cuántos objetos o arreglos cumplen ciertas condiciones. Por ejemplo, si lanzas dos dados, ¿de cuántas formas puedes obtener un 8? La combinatoria enumerativa te da las herramientas para resolver este tipo de problemas.
Ejemplo: Si lanzas 2 dados, ¿de cuántas formas puedes obtener 8? Las combinaciones son (2,6), (3,5), (4,4), (5,3), (6,2). Hay 5 formas. Si lanzas 3 dados, ¿cuántas formas hay de obtener 10? La combinatoria nos ayuda a encontrar la respuesta sin tener que listar todas las posibilidades.
Diseños y Estructuras: Teoría del Diseño
Esta área estudia cómo organizar colecciones de elementos con propiedades específicas. Por ejemplo, cómo organizar un grupo de estudiantes para que cada par de ellos se encuentre en un equipo diferente.
Conexiones con la Informática y la Física
La combinatoria es fundamental en la informática para analizar la eficiencia de los algoritmos (pasos para resolver un problema). También se usa en la física estadística para entender cómo se comportan grandes grupos de partículas.
Principios Básicos para Contar
Estos principios son reglas sencillas que nos ayudan a contar las posibilidades en diferentes situaciones.
Principio de la Suma
Si tienes dos tareas que no pueden ocurrir al mismo tiempo, y la primera se puede hacer de n1 formas y la segunda de n2 formas, entonces hay n1 + n2 formas de hacer una de las dos tareas.
Ejemplo: Una pareja busca casa. En un lugar les ofrecen 2 modelos diferentes. En otro lugar, les ofrecen 3 modelos diferentes. ¿Cuántas opciones de vivienda tienen en total? Solución: 2 (del primer lugar) + 3 (del segundo lugar) = 5 opciones diferentes.
Principio del Producto (o Multiplicación)
Si una tarea se puede dividir en varios pasos, y el primer paso se puede hacer de N1 formas, el segundo de N2 formas, y así sucesivamente, entonces el número total de formas de completar la tarea es N1 × N2 × ... × Nr.
Ejemplo 1: Tienes 3 camisas y 4 pantalones. ¿Cuántas combinaciones diferentes de ropa puedes hacer? Solución: 3 camisas × 4 pantalones = 12 combinaciones posibles.
Ejemplo 2: Si lanzas un dado de 6 caras y sacas una carta de un mazo de 52 cartas. ¿Cuántos resultados posibles hay? Solución: 6 (resultados del dado) × 52 (resultados de la carta) = 312 resultados posibles.
Principio de Permutación
Este principio se usa cuando el orden de los objetos SÍ importa y seleccionas un número específico de objetos de un grupo más grande.
Fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n P r = \frac{n!}{(n - r)!} Donde:
- n = número total de objetos
- r = número de objetos seleccionados
- ! = factorial (como explicamos antes)
Ejemplo: En un concurso con 15 participantes, ¿de cuántas formas se pueden designar los cuatro primeros lugares (1º, 2º, 3º, 4º)? Solución: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 15 P 4 = \frac{15!}{(15 - 4)!} = \frac{15!}{11!} = 15 \times 14 \times 13 \times 12 = 32760 Hay 32,760 formas diferentes de designar los cuatro primeros lugares.
Principio de Combinación
Este principio se usa cuando el orden de los objetos NO importa.
Fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): n C r = \frac{n!}{r!(n – r)!}
Ejemplo: Una compañía quiere usar 3 colores de un total de 7 disponibles para identificar cada una de las 42 partes de un producto, de modo que cada parte tenga una combinación de 3 colores diferentes. ¿Será suficiente este código de colores? Solución: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 7 C 3 = \frac{7!}{3!(7 – 3)!} = \frac{7!}{3!4!} = \frac{5040}{6 \times 24} = \frac{5040}{144} = 35 Solo hay 35 combinaciones posibles de 3 colores de un total de 7. Como necesitan identificar 42 partes, este código de colores NO es suficiente.
Galería de imágenes
-
Diagrama de flujo para identificar el tipo de problema combinatorio.
Véase también
En inglés: Combinatorics Facts for Kids
- Permutación
- Coeficiente binomial
- Teoría de Ramsey
- Combinaciones con repetición
- Factorial de un número
