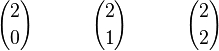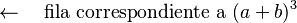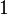Triángulo de Pascal para niños

Enciclopedia para niños

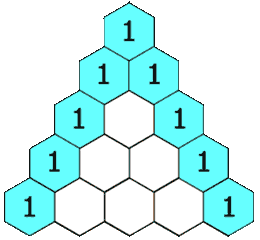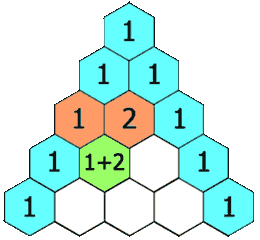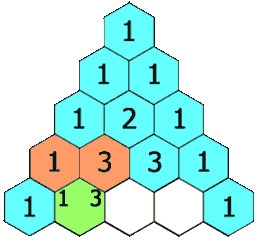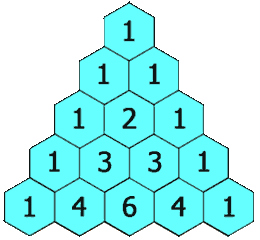
En las matemáticas, el triángulo de Pascal o triángulo de Tartaglia es una forma especial de organizar números en un patrón triangular. Estos números son los coeficientes binomiales, que aparecen cuando multiplicamos expresiones como (a+b) varias veces.

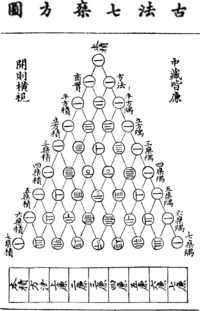
Este triángulo lleva el nombre del matemático francés Blaise Pascal, quien lo estudió a fondo en 1654 en su libro Tratado del triángulo aritmético. Aunque matemáticos de la India, China, Persia, Alemania e Italia ya conocían algunas de sus propiedades mucho antes, Pascal fue quien exploró muchas de sus aplicaciones y organizó toda la información de manera completa.

El triángulo de Pascal se puede extender a más dimensiones. Por ejemplo, en tres dimensiones se le llama pirámide de Pascal o tetraedro de Pascal. Las versiones más generales se conocen como símplex de Pascal.

Contenido

Historia del Triángulo de Pascal
¿Cómo se construye el Triángulo de Pascal?
Propiedades del Triángulo de Pascal
Generalizaciones del Triángulo de Pascal
El Triángulo de Pascal en Programación
Galería de imágenes
Véase también

Historia del Triángulo de Pascal

Triángulo aritmético chino

La primera vez que se vio un triángulo con coeficientes binomiales fue en el siglo X. Apareció en los comentarios de un libro antiguo de la India llamado Chandas Shastra, que trataba sobre la prosodia del sánscrito y fue escrito por Pingala alrededor del año 200 a.C.

Más tarde, los matemáticos persas Al-Karaji (953–1029) y Omar Khayyám (1048–1131) estudiaron las propiedades de este triángulo. Por eso, en Irán se le conoce como el triángulo Khayyam-Pascal o simplemente el triángulo Khayyam. Ellos ya conocían muchos teoremas relacionados, como el teorema del binomio.

En China, el matemático Jia Xian (1010–1070) ya conocía este triángulo en el siglo XI. En el siglo XIII, Yang Hui (1238–1298) presentó el triángulo aritmético, que es igual al triángulo de Tartaglia. Por eso, en China se le llama triángulo de Yang Hui.

En Europa, Petrus Apianus (1495–1552) publicó el triángulo en la portada de su libro de cálculos comerciales Rechnung en 1527. Este es el primer registro del triángulo en Europa. En Italia, se le conoce como el triángulo de Tartaglia, en honor al matemático italiano Niccolò Fontana Tartaglia (1500–1577). Otros matemáticos como Michael Stifel (1486-1567) y François Viète (1540-1603) también lo estudiaron.

Blaise Pascal, en su Traité du triangle arithmétique (Tratado del triángulo aritmético) de 1654, recopiló varios descubrimientos sobre el triángulo. Los usó para resolver problemas de teoría de la probabilidad. Demostró 19 de sus propiedades, algunas de las cuales ya se conocían pero no se habían demostrado formalmente. Para probarlas, Pascal usó una técnica llamada inducción matemática. También demostró la conexión entre el triángulo y la fórmula del binomio. Fue Pierre Raymond de Montmort (1708) quien lo llamó Tabla del Sr. Pascal para las combinaciones, y Abraham de Moivre (1730) lo llamó "Triangulum Arithmeticum PASCALIANUM" (en latín: "Triángulo aritmético de Pascal"), que es el nombre que usamos hoy en día.

¿Cómo se construye el Triángulo de Pascal?

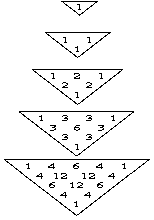
El triángulo de Pascal se construye siguiendo un patrón sencillo. Se empieza con el número «1» en la parte de arriba, que es la fila cero. Debajo de este «1», se colocan dos «1»s en la fila uno.

Para las filas siguientes, cada número se obtiene sumando los dos números que están justo encima de él. Si no hay un número encima (en los bordes del triángulo), se considera que hay un cero. Por eso, los números en los bordes del triángulo siempre son «1».

Cada número en el triángulo es la suma de los dos que están situados por encima de él.

Uso del Triángulo de Pascal

Este triángulo es muy útil para desarrollar las potencias de binomios. Un binomio es una expresión con dos términos, como (a+b). Cuando elevamos un binomio a una potencia, por ejemplo, (a+b)ⁿ, el triángulo de Pascal nos da los números (coeficientes) que acompañan a cada término en el resultado.

Esta relación se conoce como el binomio de Newton. Los números de cada fila del triángulo de Pascal corresponden a los coeficientes de la expansión de (a+b)ⁿ.

Conexión con el Binomio de Newton

Las cifras en cada fila del triángulo de Pascal son los coeficientes de las potencias del binomio de Newton. Veamos algunos ejemplos:

(a+b)² = 1a² + 2ab + 1b²
(a+b)³ = 1a³ + 3a²b + 3ab² + 1b³

Si observas, los números en negrita (1, 2, 1) corresponden a la fila 2 del triángulo, y (1, 3, 3, 1) a la fila 3. En general, para (a+b)ⁿ, los coeficientes se encuentran en la fila "n" del Triángulo de Pascal (si la primera fila es la fila 0).

Combinatoria en el Triángulo de Pascal

La forma en que se construye el triángulo está relacionada con los coeficientes binomiales y la combinatoria. La regla de Pascal nos dice que los números (o "nodos") de una fila del triángulo se pueden calcular usando la fórmula de combinaciones.

Esta fórmula se escribe como 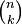$\tbinom n k$ y significa "n sobre k". Aquí, n es el número de la fila (empezando desde 0) y k es la posición del número dentro de esa fila (también empezando desde 0).

Por ejemplo, para el binomio (a+b)³, los coeficientes son 1, 3, 3, 1. Estos coeficientes se pueden expresar con la fórmula de combinaciones así:

{0 \choose 0}

{1 \choose 0}\quad \quad \quad {1 \choose 1}

{2 \choose 0}\quad \quad \quad {2 \choose 1}\quad \quad \quad{2 \choose 2}

{3 \choose 0}\quad \quad \quad{3 \choose 1}\quad \quad \quad{3 \choose 2}\quad \quad \quad{3 \choose 3}

\quad \leftarrow \quad \text{fila correspondiente a }(a+b)^3

Y el triángulo correspondiente sería:

1

1 \quad \quad 1

1 \quad \quad 2 \quad \quad 1

1 \quad \quad 3 \quad \quad 3 \quad \quad 1

\quad \leftarrow \quad \text{fila correspondiente a } (a+b)^3

Propiedades del Triángulo de Pascal

Triángulo de Pascal con algunas casillas coloreadas. Se puede observar como se distribuyen los valores simétricamente alrededor del eje vertical. Los valores de las casillas de ambos lados (en amarillo, verde y rojo) tienen el mismo valor debido a la propiedad de simetría

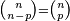\scriptstyle {n\choose {n-p}} = {n\choose p}

. Las casillas exteriores (en azul), tienen valor nulo, y las casillas en violeta, proporcionan un ejemplo de la regla de Pascal.

El triángulo de Pascal tiene varias propiedades interesantes:

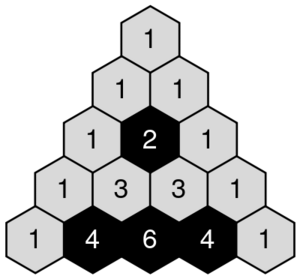
Simetría: Los números en cada fila son simétricos. Esto significa que si miras una fila, los números de un lado son un espejo de los números del otro lado. Por ejemplo, en la fila 4, los números son 1, 4, 6, 4, 1. El 4 de la izquierda es igual al 4 de la derecha.
Valores Cero: Fuera del triángulo, los valores se consideran cero. Esto es porque no hay combinaciones posibles en esas posiciones.
Regla de Construcción: La regla principal para construir el triángulo (sumar los dos números de arriba para obtener el de abajo) es una propiedad fundamental de los coeficientes binomiales.
Suma de Filas: Si sumas todos los números de cualquier fila del triángulo, el resultado siempre será una potencia de 2. Por ejemplo, la suma de la fila 0 es 1 (2⁰), la suma de la fila 1 es 1+1=2 (2¹), la suma de la fila 2 es 1+2+1=4 (2²), y así sucesivamente.

Aproximación al triángulo de Sierpinski obtenida coloreando de negro las casillas del Triángulo de Pascal que contienen un número par y de gris aquéllas que contienen un número impar.

Generalizaciones del Triángulo de Pascal

Ejemplo combinacional de coeficiente trinomial.

Así como el triángulo de Pascal se basa en potencias de (a+b), podemos pensar en potencias de expresiones con más términos, como (a+b+c). Cuando elevamos (a+b+c) a una potencia n, obtenemos una suma de términos con coeficientes especiales llamados coeficientes trinomiales.

Estos coeficientes se pueden organizar en una estructura tridimensional que se llama pirámide de Pascal. Es como una pirámide infinita con secciones triangulares. El valor de cada número en la pirámide es la suma de los tres números que están justo encima de él.

Pirámide de Pascal. Se han dibujado las primeras secciones a partir de la cumbre.

En esta pirámide, si la giras 120 grados alrededor de un eje vertical que pasa por la punta, se ve igual. Además, el triángulo de Pascal normal aparece en las tres caras de la pirámide.

Este concepto se puede extender a cualquier número de dimensiones, aunque ya no es posible dibujarlas de forma sencilla.

El Triángulo de Pascal en Programación

Para crear el triángulo de Pascal usando código de programación, se usa la propiedad de que cada número en el triángulo es un coeficiente de combinación. La fórmula para calcular un coeficiente de combinación es: C(x, y) = x! / (y! * (x-y)!), donde "!" significa factorial (por ejemplo, 5! = 5 * 4 * 3 * 2 * 1).

Aquí te mostramos cómo se puede programar el triángulo de Pascal en diferentes lenguajes:

Código en Java

import java.util.Scanner;

public class TrianguloPascal {

        public static void main(String[] args) {
                Scanner entrada = new Scanner(System.in);
                System.out.print("Indica el número de filas que desee: ");
                crearTriangulo(entrada.nextInt());
                entrada.close();
        }
        
        private static long factorial(int n1) {
                long miNum = 1;
                for(int i=1;i<=n1;i++) {
                        miNum*=i;
                }
                return miNum;
        }
        
        private static int combinatoria(int n1, int n2) {
                int resultado = 0;
                resultado = (int) (factorial(n1) / (factorial(n2)*factorial(n1-n2)));
                return resultado;
        }
        
        public static void crearTriangulo(int n_filas) {
                for(int fila=1;fila<=n_filas;fila++) {
                        for(int i=0;i<(n_filas-fila);i++) {
                                System.out.print(" ");
                        }
                        if(fila == 1) {
                                System.out.println("1 1");
                        }else {
                                for(int i=0;i<(fila+1);i++) {
                                        System.out.print(combinatoria(fila, i) + " ");
                                }
                                System.out.println();
                        }
                }
        }

}

Código en Python

# Doing the Pascal's Triangle using Python
def factorial(num):
    if num > 0:
        # Doing the factorial using recursion
        return int(num*factorial(num-1))
    else:
        return 1

def combinatoria(num1, num2):
    return int(factorial(num1) / (factorial(num2)*factorial(num1-num2)))

def crearTriangulo(n_filas):
    for fila in range(n_filas):
        for j in range(n_filas-fila+1):
            print(" ", end="")
        if fila == 0:
            print("1 1")
        else:
            for j in range(fila+2):
                print(combinatoria(fila+1, j), end=" ")
            print()

crearTriangulo(int(input("Indica el número de filas que desee: ")))

Código en C++

#include<iostream>

long factorial(int x){
        if(x > 0){
                return x * factorial(x-1); //Recursividad
        }else{
                return 1;
        }
}
int combinatoria(int num1, int num2){
        return ((int) factorial(num1))/ (factorial(num2)*factorial(num1-num2));
}
void imprimirTriangulo(int filas){
        for(int i=1;i<=filas;i++){
                for(int j=0;j<(filas-i);j++){
                        std::cout<<" ";
                }
                if(i == 1){
                        std::cout<<"1 1"<<std::endl;
                }else{
                        for(int j=0;j<=i;j++){
                                std::cout<<combinatoria(i, j)<< " ";
                        }
                        std::cout <<std::endl;
                }
        }
}
int main(){
        int filas = 0;
        std::cout<<"Escribe el número de niveles que desea: "<<std::endl;
        std::cin >> filas;
        imprimirTriangulo(filas);
    return 0;
}

Galería de imágenes

Triángulo de Pascal para n=10.

Véase también

En inglés: Pascal's triangle Facts for Kids

Coeficiente binomial
Teorema del binomio
Triángulo de Floyd

Obtenido de «https://ninos.kiddle.co/index.php?title=Triángulo_de_Pascal&oldid=5043092»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Triángulo de Pascal para Niños. Enciclopedia Kiddle.