Álgebra abstracta para niños

El álgebra abstracta es una parte de las matemáticas que estudia las estructuras matemáticas como los grupos, los anillos y los cuerpos. También se le conoce a veces como álgebra moderna o álgebra superior.

Muchas de estas estructuras se definieron de forma precisa en el siglo XIX. El estudio del álgebra abstracta surgió porque se necesitaba más exactitud en las definiciones matemáticas. En esta rama del álgebra, los elementos que se combinan con diferentes operaciones no siempre son números. Por eso, el álgebra abstracta no es solo una extensión de la aritmética (que trata con números).

Estudiar el álgebra abstracta ha ayudado a entender mejor las ideas lógicas que son la base de todas las matemáticas y de las ciencias naturales. Hoy en día, se usa en casi todas las áreas de las matemáticas. Además, los matemáticos descubrieron que estructuras lógicas que parecían diferentes a menudo se pueden describir de la misma manera usando un pequeño grupo de reglas básicas.

El término álgebra abstracta se usa para diferenciarla del álgebra elemental o del álgebra que se aprende en la escuela. El álgebra elemental enseña las reglas para trabajar con fórmulas y expresiones que usan números reales y números complejos. Durante la primera mitad del siglo XX, el álgebra abstracta se conocía como "álgebra moderna".

¿Cómo surgió el álgebra abstracta?

Antes del siglo XIX, el álgebra se centraba en cómo resolver ecuaciones con polinomios (expresiones con letras y números). El álgebra abstracta empezó a desarrollarse en el siglo XIX cuando surgieron problemas más complejos y nuevas formas de resolverlos.

Los problemas y ejemplos que dieron origen al álgebra abstracta venían de diferentes áreas de las matemáticas, como la teoría de números, la geometría y el análisis. Al principio, las teorías que hoy forman parte del álgebra abstracta eran solo un conjunto de ideas sueltas. Con el tiempo, encontraron un tema en común que las unió, y finalmente se organizaron bajo un conjunto de conceptos compartidos. Esta unión ocurrió a principios del siglo XX y llevó a las definiciones formales de estructuras como grupos, anillos y cuerpos.

Los inicios del álgebra elemental

El estudio de las ecuaciones con polinomios, también llamadas ecuaciones algebraicas, tiene una historia muy larga. Hace unos 3700 años, los babilonios ya podían resolver ecuaciones de segundo grado (cuadráticas) que se presentaban como problemas. En esa época, el álgebra se expresaba con palabras, y así fue hasta el siglo XVI.

Muhammad ibn Mūsā al-Khwārizmī fue quien dio origen a la palabra "álgebra" alrededor del año 830 d.C., pero su trabajo también se basaba en el álgebra retórica (con palabras). El álgebra que usa solo símbolos apareció con la obra de François Viète en 1591, llamada Nueva Álgebra. Incluso en esa obra, algunas palabras se escribían en lugar de usar símbolos, algo que cambió con La Géométrie de Descartes en 1637.

El estudio formal de cómo resolver ecuaciones con símbolos llevó a Leonhard Euler a aceptar conceptos que antes se consideraban "sin sentido", como los números negativos y los números imaginarios, a finales del siglo XVIII. Sin embargo, la mayoría de los matemáticos europeos no aceptaron completamente estas ideas hasta mediados del siglo XIX.

En 1830, George Peacock escribió el Tratado de Álgebra, que fue el primer intento de basar el álgebra solo en símbolos. Él diferenció una nueva álgebra simbólica de la antigua álgebra aritmética. En el álgebra aritmética, una resta como solo se podía hacer si era mayor o igual que . Pero en el álgebra simbólica, todas las reglas de las operaciones se mantenían sin restricciones.

El comienzo de la teoría de grupos

Varias áreas de las matemáticas llevaron al estudio de los grupos. Por ejemplo, el trabajo de Lagrange en 1770 sobre las soluciones de ecuaciones de quinto grado llevó al grupo de Galois de un polinomio. El estudio de Gauss en 1801 sobre el pequeño teorema de Fermat ayudó a entender los enteros módulo n y los conceptos de grupo cíclico y grupo abeliano.

En 1872, el programa de Klein, llamado programa Erlangen, estudió la geometría y llevó a los grupos de simetría, como el Grupo euclídeo. En 1874, Lie introdujo la teoría de los grupos de Lie, con el objetivo de crear una "teoría de Galois para ecuaciones diferenciales".

El concepto abstracto de grupo se desarrolló poco a poco a mediados del siglo XIX. Évariste Galois fue el primero en usar el término "grupo" en 1832, refiriéndose a una colección de transformaciones que se podían combinar entre sí. El trabajo de Arthur Cayley en 1854, Sobre la teoría de grupos, definió un grupo como un conjunto con una operación que cumple ciertas propiedades, como la asociatividad.

En 1870, Kronecker definió una operación abstracta que era cerrada, conmutativa, asociativa y tenía una propiedad de cancelación, similar a las reglas modernas para un grupo abeliano finito. La definición de grupo de Weber en 1882 incluía una operación binaria cerrada que era asociativa y tenía cancelación por ambos lados. Walther von Dyck en 1882 fue el primero en exigir que los elementos tuvieran inversos como parte de la definición de un grupo.

Una vez que surgió este concepto de grupo abstracto, los resultados matemáticos se expresaron de esta nueva forma. Por ejemplo, el teorema de Sylow fue demostrado de nuevo por Frobenius en 1887 directamente a partir de las reglas de un grupo finito. Otto Hölder fue muy importante en esta área, definiendo los grupos cociente en 1889 y los automorfismos de grupo en 1893, así como los grupos simples.

Los inicios de la teoría de anillos

La teoría de los anillos no conmutativos (donde el orden de la multiplicación importa) comenzó con la extensión de los números complejos a los números hipercomplejos. Un ejemplo importante son los cuaterniones de William Rowan Hamilton en 1843. Poco después, surgieron muchos otros sistemas numéricos.

En 1844, Hamilton presentó los bicuaterniones, Cayley introdujo los octoniones, y Grassman las álgebras exteriores. James Cockle presentó los números bicomplejos en 1848 y los cocuaterniones en 1849. Además, Cayley introdujo las álgebras de grupo y las matrices cuadradas en la década de 1850.

Cuando ya había muchos ejemplos, el siguiente paso fue clasificarlos. En 1870, Benjamin Peirce clasificó más de 150 sistemas numéricos hipercomplejos de dimensión menor a 6 y dio una definición clara de un álgebra asociativa. En la década de 1880, Killing y Cartan demostraron que las álgebras de Lie semisimples podían dividirse en partes más simples y clasificaron todas las álgebras de Lie simples.

En el caso de los anillos conmutativos (donde el orden de la multiplicación no importa), varias áreas llevaron a su teoría. En 1828 y 1832, Gauss formuló los enteros gaussianos y demostró que tienen una factorización única. El estudio del último teorema de Fermat llevó a los enteros algebraicos. En 1847, Gabriel Lamé pensó que había demostrado el teorema de Fermat, pero su prueba tenía un error porque asumió que todos los campos ciclotómicos tenían factorización única, lo cual no era cierto.

En 1846 y 1847, Kummer introdujo los números ideales y demostró la factorización única en primos ideales para campos ciclotómicos. Dedekind extendió esto en 1871 para demostrar que cada ideal en el dominio de los enteros de un campo numérico algebraico es un producto único de primos ideales, lo que fue un paso importante para la teoría de dominio de Dedekind. En general, el trabajo de Dedekind creó el campo de la teoría algebraica de números.

¿Qué estudia el álgebra abstracta?

¿Cómo se define?

Birkhoff y McLane, dos matemáticos, nos dicen:

"Se puede definir el álgebra abstracta como el estudio de las propiedades de los sistemas algebraicos que se conservan en los isomorfismos."

Vid pág. 37 de su Álgebra Moderna (1954), Barcelona

Esto significa que el álgebra abstracta busca entender las características de los sistemas matemáticos que no cambian, incluso si los elementos de esos sistemas se transforman de una manera específica (llamada isomorfismo).

Históricamente, algunos temas surgieron en otras áreas de las matemáticas, como los espacios lineales o el álgebra de Boole. Después, se les dieron reglas básicas (axiomas) y se estudiaron por sí mismos dentro del álgebra abstracta. Por eso, esta materia tiene muchas conexiones importantes con otras ramas de las matemáticas y con otras ciencias.

Tipos de estructuras algebraicas

El álgebra abstracta clasifica los sistemas matemáticos según las operaciones que tienen y las reglas que siguen. Aquí hay algunos ejemplos:

• Con una sola operación:
  • Magmas: Un conjunto con una operación.
  • Semigrupos: Magmas donde la operación es asociativa.
  • Cuasigrupos: Magmas donde se pueden "deshacer" las operaciones.
  • Monoides: Semigrupos con un elemento especial que no cambia nada al operarlo.
  • Grupos: Monoides donde cada elemento tiene un "inverso" que lo devuelve al elemento especial.

• Con dos o más operaciones:
  • Anillos y cuerpos: Conjuntos con dos operaciones que se parecen a la suma y la multiplicación.
  • Módulos y Espacios vectoriales: Estructuras que combinan un grupo con una multiplicación por "escalares" (números).
  • Álgebras asociativas y Álgebras de Lie: Espacios vectoriales con una multiplicación especial.
  • Retículos y álgebras de Boole: Estructuras que se usan en lógica y en el diseño de circuitos.

El Álgebra universal es un campo de las matemáticas que ayuda a comparar las diferentes estructuras algebraicas. Además de las anteriores, existen otras estructuras:

• Álgebra homológica.
• Lenguajes formales (como las reglas para construir frases en un idioma).
• Álgebra sobre un cuerpo.

Un ejemplo práctico

El estudio del álgebra abstracta ha permitido a los matemáticos encontrar una descripción lógica común para conceptos que parecían muy diferentes. Por ejemplo, podemos pensar en dos operaciones distintas: la composición de funciones, como 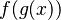, y la multiplicación de matrices, como .

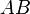Aunque parecen diferentes, estas dos operaciones son, en esencia, la misma. Podemos verlo así: multiplicar dos matrices cuadradas 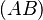por un vector de una columna, . Esto es como aplicar una función que es igual a componer 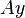con 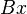, es decir, = = .

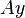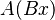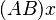Las funciones bajo composición y las matrices bajo multiplicación forman estructuras llamadas monoides. Un monoide es un conjunto donde una operación es asociativa (el orden de las operaciones no importa si hay tres o más elementos, por ejemplo, 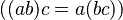) y tiene un elemento especial que no cambia nada al operarlo (llamado elemento identidad, , tal que 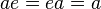para cualquier elemento ). Lo importante en el álgebra abstracta no son los elementos en sí, sino las operaciones y las reglas que siguen en esos conjuntos.

Galería de imágenes

• 

  George Peacock (1791-1858), matemático británico.

• 

  Arthur Cayley (1821-1895), matemático británico.

Véase también

En inglés: Abstract algebra Facts for Kids