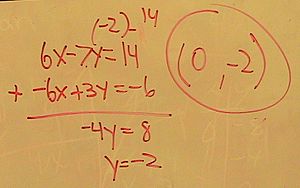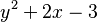Álgebra elemental para niños

Un ejemplo de problema de álgebra.

El álgebra elemental es una parte fundamental de las matemáticas. Imagina que en aritmética solo usas números y operaciones como sumar, restar, multiplicar y dividir. Pues en álgebra, ¡también usamos letras! Estas letras, como "x", "y", "a" o "b", representan números que no conocemos o que pueden cambiar. Las llamamos variables o incógnitas.

El álgebra elemental es muy útil porque:

Nos permite escribir reglas generales para los números. Por ejemplo, sabemos que si sumas dos números, no importa el orden, el resultado es el mismo (como 2 + 3 = 3 + 2). En álgebra, esto se escribe como $\, a + b = b + a$ . Así, podemos entender mejor cómo funcionan los números.
Nos ayuda a encontrar números que no conocemos. Si tenemos un problema donde un valor es desconocido, podemos usar una letra para representarlo. Luego, con ecuaciones, podemos descubrir cuál es ese valor.
Nos permite explorar cómo se relacionan diferentes cantidades. Por ejemplo, si vendes "x" boletos y cada uno te da 3 dólares de ganancia, pero tienes un gasto fijo de 10 dólares, tu ganancia total sería 3x - 10 dólares.

Estas ideas son el corazón del álgebra elemental. Es diferente del álgebra abstracta, que es un tema más avanzado que se estudia en la universidad.

En álgebra elemental, una expresión es una combinación de números, letras (variables) y operaciones. Por ejemplo:

$x + 3\,$
$y^{2} + 2x - 3\,$

Una ecuación es una afirmación que dice que dos expresiones son iguales. Algunas ecuaciones son siempre verdaderas, no importa qué valor tengan las variables (como $\, a + b = b + a$ ). A estas las llamamos identidades. Otras ecuaciones solo son verdaderas para ciertos valores de las variables, por ejemplo: 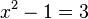$\, x^{2} - 1 = 3$ . Los valores que hacen que la ecuación sea verdadera se llaman las soluciones de la ecuación.

Símbolos en Álgebra

Símbolos de Operación

En álgebra, usamos los mismos símbolos de operación que en aritmética, ¡y algunos más!

Suma: +

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a + b \;

Resta: –

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a - b \;

Multiplicación: × o · (a veces no se escribe)

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \times b \; * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \cdot b \; * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a b \; (cuando las letras están juntas, significa multiplicación)

División: ÷ o / (también como fracción)

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a / b \; * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \div b \; * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cfrac{a}{b}

Potenciación: Un número pequeño arriba y a la derecha (exponente)

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^b \; (significa multiplicar "a" por sí misma "b" veces)

Radicación: La raíz

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{a} \; (raíz cuadrada de "a") * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt[b]{a} (raíz "b" de "a")

Logaritmos:

* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_b a

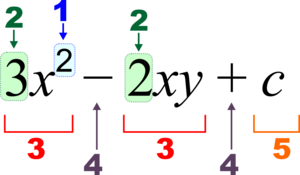
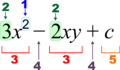
La forma en que escribimos las expresiones en álgebra sigue ciertas reglas. Por ejemplo, en la expresión 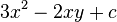$3x^2 - 2xy + c$ :

1. exponente (potencia) 2. coeficiente 3. término 4. operación 5. constante,

x, y

. variables

Un coeficiente es el número que multiplica a una variable (como el 3 en 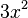$3x^2$ ). Un término es una parte de la expresión que puede estar separada por signos de suma o resta (como 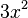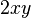$3x^2$ , $2xy$ o $c$ ). Las letras al principio del alfabeto (a, b, c) suelen ser constantes (números fijos), y las del final (x, y, z) son variables (números que pueden cambiar).

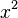Cuando un coeficiente es 1, no se escribe (por ejemplo, $1x^2$ se escribe $x^2$ ). Si el exponente es 1, tampoco se escribe (por ejemplo, 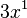$3x^1$ se escribe 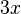$3x$ ). Si el exponente es 0, el resultado es siempre 1 (por ejemplo, 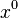$x^0$ es 1).

Símbolos de Relación

Estos símbolos nos dicen cómo se comparan dos expresiones:

< : menor que
> : mayor que
= : igual a
≠ : diferente a
≤ : menor o igual a
≥ : mayor o igual a

Símbolos de Agrupación

Estos símbolos nos ayudan a organizar las operaciones y a decidir qué hacer primero. Las operaciones dentro de ellos siempre se resuelven antes.

( ) → paréntesis
[ ] → corchetes
{ } → llaves
| | → barras (a veces para valor absoluto)

El orden para resolver operaciones con estos símbolos es: 1. Primero, lo que está dentro de los paréntesis ( ). 2. Luego, lo que está dentro de los corchetes [ ]. 3. Después, lo que está dentro de las llaves { }. 4. Finalmente, lo que está dentro de las barras | |.

Si un número está justo antes de un símbolo de agrupación, significa que se está multiplicando:

3 (5) = 3 × 5
6 [9] = 6 × 9

Expresiones Algebraicas

Término

Un término es una parte básica de una expresión algebraica. Solo contiene multiplicaciones y divisiones de números y letras. El número se llama coeficiente, y las letras forman la parte literal. Por ejemplo, en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5x^2y , 5 es el coeficiente y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2y es la parte literal. Los términos en una expresión más grande están separados por signos de suma o resta.

Término Independiente

Es un término que solo tiene un número y ninguna letra. Por ejemplo, en Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3x + 7 , el 7 es el término independiente.

Términos Semejantes

Los términos semejantes son aquellos que tienen exactamente la misma parte literal (las mismas letras con los mismos exponentes). Solo se diferencian en el coeficiente. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2x^2 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5x^2 son términos semejantes.

Solo podemos sumar y restar términos que sean semejantes. No puedes sumar $a + b$ , pero sí puedes multiplicarlos (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a \cdot b = ab ). Si en una expresión hay varios términos semejantes, puedes simplificarlos sumándolos o restándolos.

Un polinomio es una expresión algebraica donde solo hay sumas, restas y multiplicaciones, y los exponentes de las letras son números enteros positivos.

Un polinomio con un solo término se llama monomio (ej: $5x$ ).
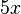Con dos términos, se llama binomio (ej: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2x + 3 ).
Con tres términos, se llama trinomio (ej: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 + 2x - 1 ).

Valor Numérico de un Polinomio

Es el resultado que obtenemos cuando reemplazamos las letras de un polinomio por números y luego hacemos todas las operaciones.

Reglas Básicas del Álgebra Elemental

Propiedades de las Operaciones

Suma (+)

* Es conmutativa: $\, a + b = b + a$ (el orden no importa). * Es asociativa: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, (a + b) + c = a +(b + c) (cómo agrupas no importa). * Tiene una operación inversa, la sustracción: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, (a + b)- b = a . Restar es como sumar un número negativo. * Tiene un elemento neutro (el 0): Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, a + 0 = a (sumar 0 no cambia el número).

Multiplicación (× o ·)

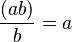* Es conmutativa: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, (a \cdot b ) = (b \cdot a) . * Es asociativa: $\, (a \cdot b) \cdot c = a \cdot (b \cdot c)$ . * Se puede abreviar juntando las letras: $a \cdot b \equiv ab$ . * Tiene una operación inversa (para números que no son cero), la división: $\frac{(ab)}{b} = a$ . Dividir es como multiplicar por el recíproco. * Tiene un elemento neutro (el 1): 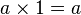$a \times 1 = a$ (multiplicar por 1 no cambia el número). * Es distributiva con respecto a la suma: 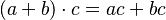$\, (a + b) \cdot c = ac + bc$ (puedes "distribuir" la multiplicación).

Potenciación

* Se escribe 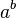$\, a^{b}$ . * Es una multiplicación repetida: 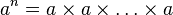$a^{n} = a \times a \times \ldots \times a$ (n veces). * Tiene una operación inversa, el logaritmo. * Es distributiva con respecto a la multiplicación: 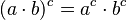$\, (a \cdot b)^{c} = a^{c} \cdot b^{c}$ . * Cuando multiplicas potencias con la misma base, sumas los exponentes: 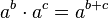$\ {a^{b}} \cdot {a^{c}} = a^{b + c}$ . * Cuando elevas una potencia a otra potencia, multiplicas los exponentes: 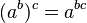$\, (a^{b})^{c} = a^{bc}$ . * No es conmutativa (generalmente Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, a^{b} \ne b^{a} ) ni asociativa.

Orden de las Operaciones

Para resolver una expresión, siempre debes seguir un orden específico: 1. Primero, resuelve lo que está dentro de los símbolos de agrupación (paréntesis, corchetes, llaves). 2. Luego, calcula las potencias y raíces. 3. Después, haz las multiplicaciones y divisiones (de izquierda a derecha). 4. Finalmente, realiza las sumas y restas (de izquierda a derecha).

Reglas de la Igualdad

La relación de igualdad (=) tiene estas propiedades:

Si $\, a = b$ y $\, c = d$ , entonces $\, a + c = b + d$ y $\, ac = bd$ .
Si $\,a = b$ , entonces $\, a + c = b + c$ (puedes sumar lo mismo a ambos lados).
Si dos símbolos son iguales, puedes reemplazar uno por el otro.
Si $\, a + c = b + c$ , entonces $\, a = b$ (puedes restar lo mismo a ambos lados).
Si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, a \cdot c = b \cdot c y $\, c$ no es cero, entonces $\, a = b$ (puedes dividir por lo mismo a ambos lados, si no es cero).

Reglas de la Desigualdad

La relación de desigualdad (<, >, ≤, ≥) tiene estas propiedades:

De transitividad: si 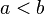$\, a < b$ y $\, b < c$ , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, a < c .
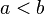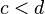Si $\, a < b$ y $\, c < d$ , entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, a + c < b + d .
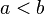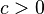Si $\, a < b$ y $\, c > 0$ (c es positivo), entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, ac < bc (la desigualdad se mantiene).
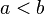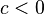Si $\, a < b$ y $\, c < 0$ (c es negativo), entonces Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \, bc < ac (la desigualdad se invierte).

Regla de los Signos

Cuando multiplicas o divides números positivos (+) y negativos (-), se cumplen estas reglas:

Positivo por negativo = Negativo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): + \cdot - = - )
Positivo por positivo = Positivo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): + \cdot + = + )
Negativo por negativo = Positivo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): - \cdot - = + )
Negativo por positivo = Negativo (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): - \cdot + = - )

Galería de imágenes

Un ejemplo de problema de álgebra.
1. Exponente (potencia) 2. Coeficiente 3. Término 4. Operación 5. Constante, x, y. Variables

Véase también

En inglés: Elementary algebra Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Álgebra_elemental&oldid=4687735»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Álgebra elemental para Niños. Enciclopedia Kiddle.