Conjetura de Kepler para niños
La conjetura de Kepler es una idea propuesta por el famoso científico alemán Johannes Kepler en 1611. Él pensó que, si apilas esferas del mismo tamaño, como naranjas o pelotas de tenis, la forma más eficiente de hacerlo para que ocupen el menor espacio posible es un tipo de apilamiento piramidal. Este tipo de apilamiento, llamado "empaque cerrado", logra una densidad de aproximadamente el 74%. Esto significa que el 74% del espacio está ocupado por las esferas y el resto es aire.
Durante mucho tiempo, esta idea fue solo una conjetura, es decir, una suposición muy bien pensada que necesitaba ser demostrada. En 1998, un matemático llamado Thomas Hales anunció que había logrado demostrar la conjetura de Kepler. Su prueba fue muy compleja e incluyó muchos cálculos hechos con computadoras.
Los expertos que revisaron el trabajo de Hales estaban casi seguros de que era correcto, pero no podían revisar cada uno de los miles de millones de cálculos que la computadora había hecho. Por eso, Hales y su equipo crearon un proyecto llamado Flyspeck. Este proyecto consistía en un programa de computadora diseñado para verificar, paso a paso, cada parte de la prueba matemática. En 2014, el equipo de Hales anunció que el programa había revisado toda la prueba y no había encontrado ningún error.
Finalmente, en junio de 2017, la demostración formal de la Conjetura de Kepler fue aceptada y publicada en una revista científica importante, lo que la convirtió en un teorema, es decir, una verdad matemática demostrada.
Contenido
¿Qué es la Conjetura de Kepler?
Imagina que quieres llenar un recipiente grande con muchas pelotas pequeñas del mismo tamaño. La densidad de cómo las acomodas se refiere a cuánto espacio ocupan las pelotas en comparación con el espacio total del recipiente. Si quieres meter la mayor cantidad de pelotas posible, necesitas acomodarlas de la manera más compacta.
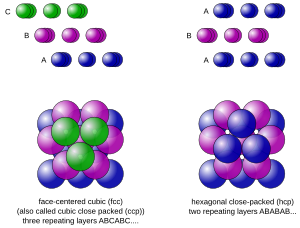
Si simplemente dejas caer las pelotas al azar, el recipiente se llenará hasta una densidad de alrededor del 65%. Pero si las organizas con cuidado, puedes lograr una densidad mucho mayor. Una forma de hacerlo es empezar con una capa de pelotas formando un patrón hexagonal. Luego, colocas la siguiente capa en los huecos de la primera, y así sucesivamente.
Existen dos maneras principales de hacer este tipo de apilamiento ordenado: el empaque cerrado cúbico y el empaque cerrado hexagonal. Ambos logran una densidad de aproximadamente 74.04%. La conjetura de Kepler afirma que esta es la mejor manera de apilar esferas iguales; ninguna otra forma de acomodarlas puede lograr una densidad mayor.
Orígenes de la Conjetura
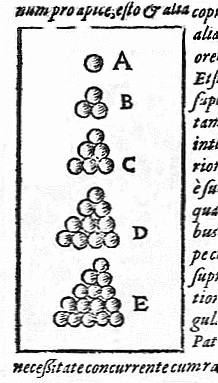
La conjetura fue mencionada por primera vez por Johannes Kepler en un escrito que hizo en 1611, llamado "Sobre el copo de nieve de seis picos". Kepler empezó a pensar en cómo se apilan las esferas gracias a una conversación que tuvo en 1606 con otro científico, Thomas Harriot.
Harriot era amigo de Walter Raleigh, un explorador y escritor, quien le había preguntado cuál era la mejor manera de apilar balas de cañón en los barcos para que ocuparan el menor espacio posible. Harriot estudió diferentes formas de apilar objetos y publicó sus ideas en 1591.
Avances en el Siglo XIX
Kepler no pudo demostrar su conjetura. El siguiente paso importante lo dio el matemático Carl Friedrich Gauss en 1831. Él demostró que la conjetura de Kepler era cierta si las esferas se organizaban en un patrón regular, como una red.
Esto significaba que, si alguien quería demostrar que la conjetura de Kepler era falsa, tendría que encontrar una forma de apilar las esferas de manera irregular que fuera más densa. Pero estudiar todos los posibles arreglos irregulares es muy complicado, y por eso la conjetura fue tan difícil de probar durante tanto tiempo.
Después de Gauss, no hubo grandes avances en la prueba de la conjetura de Kepler en el siglo XIX. En 1900, el famoso matemático David Hilbert la incluyó en su lista de 23 problemas matemáticos sin resolver, como parte del decimoctavo problema.
La Prueba de Thomas Hales
Thomas Hales, un matemático de la Universidad de Míchigan, decidió abordar la conjetura de Kepler. En 1992, con la ayuda de su estudiante Samuel Ferguson, comenzó un proyecto de investigación. Su idea era usar métodos de programación lineal para encontrar la densidad máxima de los arreglos de esferas.
Hales tuvo que analizar más de 5,000 configuraciones diferentes de esferas. Para cada una, necesitaba resolver problemas matemáticos muy complejos, ¡alrededor de 100,000 en total! Si lograba demostrar que la densidad de estas configuraciones no superaba la del empaque cerrado cúbico, entonces la conjetura de Kepler sería cierta.
En 1998, Hales anunció que había completado la prueba. Era un trabajo enorme: 250 páginas de notas y 3 gigabytes de programas de computadora, datos y resultados.
A pesar de lo inusual de una prueba tan dependiente de computadoras, una importante revista científica, Annals of Mathematics, decidió publicarla. Sin embargo, un grupo de doce expertos tardó cuatro años en revisarla. En 2003, el líder del grupo dijo que estaban "99% seguros" de que la prueba era correcta, pero no podían verificar todos los cálculos de la computadora.
La Prueba Formal con Computadoras
Para eliminar cualquier duda, en 2003 Hales inició un nuevo proyecto llamado Flyspeck. El objetivo era crear una prueba completamente formal de la conjetura de Kepler. Esto significaba que la prueba sería tan precisa que podría ser verificada por programas de computadora especiales, como HOL Light e Isabelle.
Hales pensó que este proyecto tomaría unos 20 años. Sin embargo, el 10 de agosto de 2014, se anunció que el proyecto Flyspeck estaba terminado. En 2015, Hales y 21 colaboradores presentaron un documento que afirmaba haber probado la conjetura de manera formal. Finalmente, en 2017, esta prueba formal fue aceptada y publicada en la revista Forum of Mathematics. Esto marcó un hito importante, ya que demostró que las computadoras pueden ayudar a verificar pruebas matemáticas muy complejas.
Véase también
 En inglés: Kepler conjecture Facts for Kids
En inglés: Kepler conjecture Facts for Kids