Ecuación de cuarto grado para niños

En álgebra, una ecuación de cuarto grado o ecuación cuártica es un tipo de ecuación algebraica que tiene una forma específica. Imagina que tienes una balanza y quieres encontrar un valor desconocido. En matemáticas, ese valor desconocido se representa con una letra, usualmente la x.

Una ecuación de cuarto grado se ve así:

Aquí, las letras a, b, c, d y e son números que ya conocemos. La letra x es el valor que queremos encontrar. Es muy importante que el número a no sea cero, porque si lo fuera, la ecuación ya no sería de cuarto grado, sino de un grado menor. Estos números suelen ser números reales o números complejos.

Gráfico de una función polinómica de cuarto grado.

¿Qué es una Ecuación Cuártica?

Una ecuación cuártica es una ecuación donde la potencia más alta de la incógnita (generalmente x) es 4. Esto significa que la x aparece elevada a la cuarta potencia (x⁴). Resolver una ecuación cuártica significa encontrar los valores de x que hacen que la igualdad sea verdadera.

¿Cuántas soluciones tiene una Ecuación Cuártica?

Según un principio fundamental del álgebra, una ecuación de cuarto grado siempre tiene cuatro soluciones. Estas soluciones pueden ser números reales (los que usamos para contar y medir) o números complejos (que incluyen una parte imaginaria). A veces, algunas de estas soluciones pueden ser iguales entre sí.

Propiedades Clave de las Ecuaciones Cuárticas

• Si el último número de la ecuación (el término e) tiene un signo negativo, la ecuación tendrá al menos una solución real.
• Si una solución es un número complejo, su "pareja" (llamada conjugado) también será una solución. Por ejemplo, si 2 + 3i es una solución, entonces 2 - 3i también lo será.
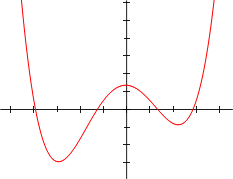
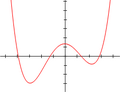
• Cuando dibujas la gráfica de una función de cuarto grado, esta puede cruzar el eje horizontal (eje X) en 0, 1, 2, 3 o 4 puntos. Cada uno de estos puntos representa una solución real de la ecuación.

¿Cómo se Resuelven las Ecuaciones Cuárticas?

Existen varios métodos para encontrar las soluciones de una ecuación de cuarto grado. Algunos de estos métodos son complejos, pero nos permiten encontrar las cuatro soluciones.

Método de Factorización: ¿Podemos Dividir el Polinomio?

La factorización es como descomponer un número grande en números más pequeños que, al multiplicarse, dan el número original. En las ecuaciones, significa reescribir el polinomio como una multiplicación de polinomios más sencillos.

Si podemos encontrar un factor lineal (como qx - p), podemos dividir el polinomio original por este factor. El resultado será un polinomio de tercer grado. Si este polinomio de tercer grado se puede resolver, habremos encontrado una de las soluciones de la ecuación cuártica. Si el residuo de la división es cero, entonces hemos encontrado una solución racional.

Método de Ferrari: Un Enfoque Histórico

El método de Ferrari es una forma de resolver ecuaciones cuárticas que fue descubierta en el siglo XVI. Para usarlo, primero se simplifica la ecuación original dividiendo todos sus términos por el número a. Luego, se resuelve una ecuación de tercer grado relacionada, llamada "ecuación cúbica resolvente".

Dependiendo de las soluciones de esta ecuación cúbica, la ecuación cuártica original tendrá diferentes tipos de soluciones:

• Puede tener dos soluciones reales y dos soluciones complejas.
• Puede tener cuatro soluciones reales distintas.
• Puede tener soluciones que se repiten (por ejemplo, una solución que aparece dos, tres o incluso cuatro veces).

Una vez que se encuentra una solución de la ecuación cúbica, se usan unas fórmulas especiales para obtener las cuatro soluciones de la ecuación cuártica original.

Método de Descartes: Otra Manera de Simplificar

El método de Descartes también busca simplificar la ecuación cuártica. Primero, se divide la ecuación por a para que el término x⁴ no tenga un número delante. Luego, se hace un "cambio de variable" para eliminar el término con x³. Esto convierte la ecuación en una forma más sencilla.

Al igual que con el método de Ferrari, se resuelve una ecuación cúbica relacionada. Una vez que se tiene una solución de esta ecuación cúbica, se usan otras fórmulas para encontrar las soluciones de la ecuación cuártica simplificada. Finalmente, se deshace el cambio de variable para obtener las soluciones de la ecuación original.

Relaciones de Cardano-Vieta: Conexiones entre Soluciones y Coeficientes

Las relaciones de Cardano-Vieta nos muestran cómo las soluciones de una ecuación cuártica están conectadas con los números a, b, c, d y e de la ecuación original. Por ejemplo:

• La suma de las cuatro soluciones es igual a -b/a.
• El producto de las cuatro soluciones es igual a e/a.

Estas relaciones son muy útiles para verificar las soluciones o para encontrar información sobre ellas sin resolver la ecuación por completo.

Casos Especiales de Ecuaciones Cuárticas

Ecuaciones Bicuadradas: Un Caso Más Sencillo

Las ecuaciones bicuadradas son un tipo especial de ecuaciones cuárticas que son más fáciles de resolver. Tienen la forma: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ax^4 + cx^2 + e = 0 Como puedes ver, no tienen el término con x³ ni el término con x.

Para resolverlas, hacemos un truco: decimos que x² es igual a una nueva letra, por ejemplo, t. Entonces, la ecuación se convierte en una ecuación de segundo grado: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): at^2 + ct + e = 0 Esta ecuación de segundo grado se puede resolver con la fórmula general. Una vez que encontramos los valores de t, recordamos que t = x², así que solo tenemos que sacar la raíz cuadrada de t para encontrar los valores de x. Esto nos dará las cuatro soluciones.

Ecuaciones Cuasisimétricas y Simétricas

Existen otros tipos especiales de ecuaciones cuárticas que tienen patrones en sus coeficientes.

• Las ecuaciones cuasisimétricas tienen una relación especial entre sus coeficientes. Se pueden resolver dividiendo por x² y haciendo un cambio de variable para simplificarlas a una ecuación de segundo grado.
• Las ecuaciones simétricas de cuarto grado tienen coeficientes que se repiten de forma simétrica (por ejemplo, ax⁴ + bx³ + cx² + bx + a = 0). También se resuelven dividiendo por x² y haciendo un cambio de variable para transformarlas en una ecuación de segundo grado.

Estos métodos especiales aprovechan la estructura de la ecuación para hacer el proceso de resolución más sencillo.

Galería de imágenes

• 

  Gráfico de una función polinómica de cuarto grado.

Véase también

En inglés: Quartic equation Facts for Kids