Cono (geometría) para niños
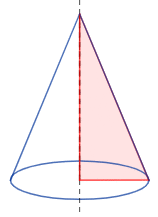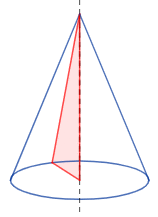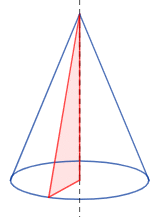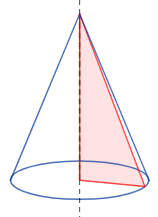
En geometría, un cono es una figura tridimensional que tiene una base circular y una superficie curva que se estrecha hasta un punto llamado vértice. Piensa en un cucurucho de helado o un gorro de fiesta: ¡esos son conos!
Un cono recto se forma cuando un triángulo rectángulo gira alrededor de uno de sus lados más cortos (llamados catetos). El círculo que se forma con el otro cateto es la base, y el punto donde se unen todas las líneas que forman el cono es el vértice.
Contenido
Partes de un Cono Geométrico
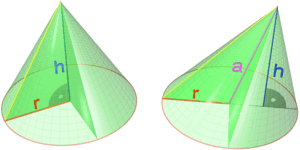
Para entender mejor un cono, es útil conocer sus partes principales.
¿Qué es la Directriz de un Cono?
La directriz es el borde de la base del cono. En un cono recto, la directriz es siempre un círculo.
¿Dónde está el Vértice del Cono?
El vértice es el punto más alto del cono, donde se encuentran todas las líneas que forman su superficie lateral. Es como la punta del gorro de fiesta.
¿Qué es la Generatriz de un Cono?
La generatriz es cualquier línea recta que va desde el vértice hasta un punto en el borde de la base (la directriz). Imagina que son las líneas que "generan" la superficie curva del cono. También se le llama altura inclinada.
¿Cuál es la Base de un Cono?
La base de un cono es la superficie plana sobre la que se apoya. En un cono circular recto, la base es un círculo.
¿Qué es la Altura de un Cono?
La altura de un cono es la distancia perpendicular desde el vértice hasta el centro de la base. Es como medir qué tan alto es el cono si lo pones sobre una mesa.
¿Qué es la Apertura de un Cono?
La apertura es el ángulo más grande que se forma entre dos generatrices opuestas en la superficie lateral del cono.
Propiedades y Medidas del Cono
Los conos tienen propiedades matemáticas que nos permiten calcular su tamaño.
¿Cómo Calcular el Área de la Superficie de un Cono?
El área total de la superficie de un cono recto se calcula sumando el área de su base y el área de su superficie lateral. La fórmula es: 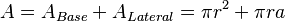 Donde:
Donde:
- r es el radio de la base (la distancia del centro al borde del círculo).
- a es la longitud de la generatriz.
La generatriz (a) se puede calcular usando el teorema de Pitágoras, ya que forma un triángulo rectángulo con la altura (h) y el radio (r) de la base: 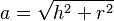 .
.
¿Cómo se Despliega un Cono Recto?
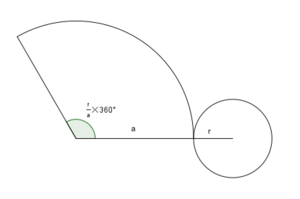
Si cortaras un cono recto y lo extendieras sobre una superficie plana, obtendrías dos figuras: un círculo (que es la base) y un sector circular (que es la superficie lateral). El sector circular es como una porción de un círculo grande.
El ángulo de este sector circular, en grados, se calcula así:
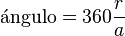 .
.
¿Cómo Calcular el Volumen de un Cono?
El volumen de un cono es la cantidad de espacio que ocupa. Es interesante saber que el volumen de un cono es exactamente un tercio del volumen de un cilindro que tenga la misma base y la misma altura.
La fórmula para el volumen 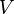 de un cono con radio
de un cono con radio  y altura
y altura 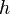 es:
es: 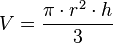
Cono Oblicuo
Un cono oblicuo es un cono cuyo vértice no está directamente sobre el centro de su base. Imagina que el vértice está "inclinado" hacia un lado.
Pueden tener una base circular o una base elíptica (con forma de óvalo). Aunque estén inclinados, la forma de calcular su volumen es la misma que la de un cono recto.
Volumen de un Cono Oblicuo
La fórmula para el volumen de un cono oblicuo de base circular es:
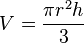
Donde  es el radio de la base y
es el radio de la base y  la altura del cono.
la altura del cono.
Si la base es elíptica, la fórmula es:
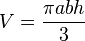
Aquí,  y
y  son los semiejes de la elipse (la mitad de sus diámetros más largo y más corto), y
son los semiejes de la elipse (la mitad de sus diámetros más largo y más corto), y  es la altura.
es la altura.
Estas fórmulas funcionan gracias a un principio llamado principio de Cavalieri, que dice que si dos cuerpos tienen la misma altura y sus secciones transversales (cortes) a la misma altura tienen la misma área, entonces tienen el mismo volumen.
Secciones Cónicas
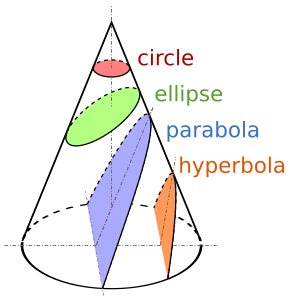
Cuando cortamos un cono con un plano (como si lo rebanáramos), las figuras que obtenemos en el corte se llaman secciones cónicas. Dependiendo del ángulo y la posición del corte, podemos obtener diferentes formas:
- Una circunferencia (si el corte es paralelo a la base).
- Una elipse (si el corte es inclinado, pero no tan inclinado como la generatriz).
- Una parábola (si el corte es paralelo a una generatriz).
- Una hipérbola (si el corte es más inclinado que la generatriz y atraviesa ambos "mantos" del cono).
Las secciones cónicas son muy importantes en la astronomía. Por ejemplo, los planetas y cometas se mueven en órbitas que son elipses, parábolas o hipérbolas alrededor del Sol. También son útiles en el diseño de objetos como antenas parabólicas y en la aerodinámica.
Ecuación de un Cono en Coordenadas
En geometría analítica, un cono se puede describir con una ecuación matemática en un sistema de coordenadas cartesianas. Una forma común de representar un cono es:
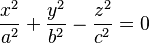
Esta ecuación describe todos los puntos (x, y, z) en el espacio que forman la superficie del cono.
Un cono es una superficie reglada, lo que significa que se puede formar moviendo una línea recta. También es una superficie que se puede "desplegar" o extender sobre un plano sin que se rompa ni se estire, como cuando abres una caja de cartón.
Véase también
 En inglés: Cone Facts for Kids
En inglés: Cone Facts for Kids