Parábola (matemática) para niños
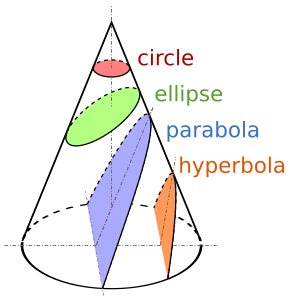
Una parábola es una curva especial que se forma cuando cortas un cono con un plano de una manera específica. Imagina que tienes un cono de helado y lo cortas con un cuchillo en cierto ángulo; la forma que aparece en la superficie de corte es una parábola.
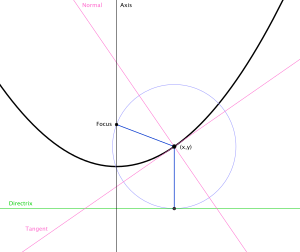
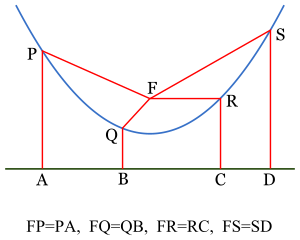
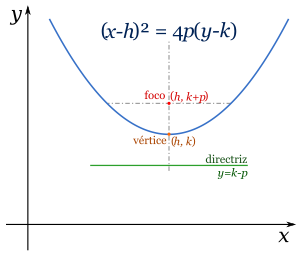
En matemáticas, una parábola se define como el conjunto de todos los puntos en un plano que están a la misma distancia de un punto fijo llamado foco y de una línea fija llamada directriz. El foco es un punto dentro de la curva, y la directriz es una línea recta fuera de ella.
Las parábolas son muy importantes en la ciencia y la ingeniería. Por ejemplo, la trayectoria que sigue una pelota lanzada al aire (si no hay viento) es una parábola. También se usan en el diseño de antenas y faros, ¡como veremos más adelante!
Contenido
Historia de la Parábola
¿Quién descubrió las parábolas?
Se cree que las secciones cónicas, incluyendo la parábola, fueron descubiertas por un matemático griego llamado Menecmo hace mucho tiempo, mientras intentaba resolver un problema de geometría.
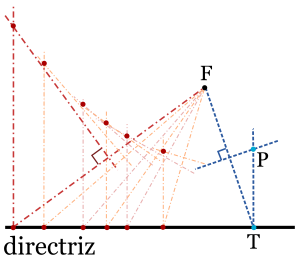
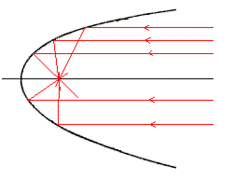
Sin embargo, el primero en usar la palabra parábola fue Apolonio de Perge, otro gran matemático griego. Él escribió un libro muy importante llamado Cónicas, donde estudió a fondo estas curvas. Apolonio descubrió una propiedad muy interesante de las parábolas: si un espejo tiene forma de parábola, los rayos de luz que llegan paralelos a su eje se reflejan y se juntan en un solo punto, ¡el foco! Esta propiedad es la base de muchas tecnologías modernas.
Otro matemático famoso, Arquímedes, también estudió las parábolas. Él investigó cómo calcular el área de una parábola, lo que fue un gran avance para su época.
Propiedades Clave de la Parábola
Como mencionamos, la parábola es el conjunto de puntos que están a la misma distancia de un punto fijo (el foco) y una línea fija (la directriz).
¿Cómo se construye una parábola?
Imagina que tienes el foco (un punto F) y la directriz (una línea recta D). Para encontrar un punto P que pertenezca a la parábola, debes asegurarte de que la distancia de P a F sea igual a la distancia de P a la línea D. Si repites este proceso con muchos puntos, ¡dibujarás una parábola!
El Vértice y el Eje
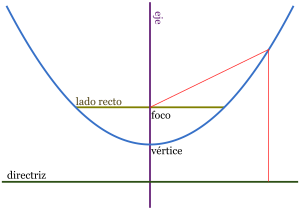
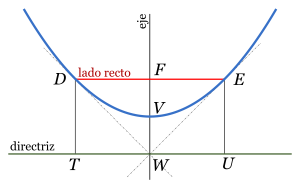
La parábola tiene un punto especial llamado vértice. Es el punto de la curva que está más cerca de la directriz. También es el punto donde la parábola cambia de dirección.
El eje de la parábola es una línea recta que pasa por el foco y el vértice, y es perpendicular a la directriz. La parábola es simétrica respecto a este eje, lo que significa que si la doblas por la mitad a lo largo del eje, ambas mitades coincidirían perfectamente.
La distancia entre el vértice y el foco se llama distancia focal.
El Lado Recto
El lado recto es un segmento de línea que pasa por el foco, es paralelo a la directriz y tiene sus extremos en la parábola. Su longitud es siempre 4 veces la distancia focal.
¿Todas las parábolas son iguales?
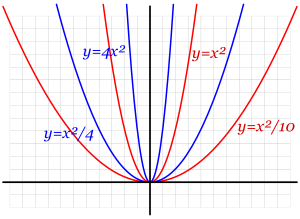
¡Sí! Aunque parezca que algunas parábolas son más anchas o más estrechas que otras, en realidad todas las parábolas tienen la misma forma. La diferencia que vemos es solo una cuestión de escala, como si estuviéramos viendo la misma parábola a través de una lupa con diferente aumento.
Aplicaciones Prácticas de las Parábolas
Las parábolas tienen muchas aplicaciones en el mundo real gracias a su propiedad de reflejar.
- Antenas Parabólicas y Radiotelescopios: Estas antenas tienen forma de parábola. Recogen las señales débiles que vienen de lejos (como las de los satélites o las estrellas) y las concentran en un solo punto: el foco. Allí se coloca un receptor que capta la señal.
- Cocinas Solares y Centrales de Energía Solar: Los reflectores parabólicos pueden concentrar los rayos del sol en un punto, generando mucho calor. Esto se usa en cocinas solares para cocinar alimentos o en grandes centrales para producir energía eléctrica.
- Faros de Automóviles y Linternas: Si colocas una bombilla en el foco de un espejo parabólico, la luz que emite se reflejará en un haz paralelo. Esto es ideal para los faros de los coches o las linternas, ya que envían la luz muy lejos y de forma concentrada.
-
La parábola refleja sobre el foco los rayos paralelos al eje. Análogamente, un emisor situado en el foco, enviará un haz de rayos paralelos al eje.
-
Los radiotelescopios concentran los haces de señales en un receptor situado en el foco. El mismo principio se aplica en una antena de radar.
-
Cocina solar de concentrador parabólico. El mismo método se emplea en las grandes centrales captadoras de energía solar.
-
Los faros de los automóviles envían haces de luz paralelos, si la bombilla se sitúa en el foco de una superficie parabólica.
Ecuaciones de la Parábola
En geometría analítica, podemos describir las parábolas usando ecuaciones. Esto nos permite dibujarlas en un plano de coordenadas y estudiar sus propiedades de forma matemática.
Parábolas con Vértice en el Origen
Una de las formas más simples de una parábola es cuando su vértice está en el punto (0,0) (el origen del plano) y su eje coincide con el eje Y. Su ecuación es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = ax^2
Aquí, la letra a controla qué tan "abierta" o "cerrada" parece la parábola. Si a es positivo, la parábola se abre hacia arriba. Si a es negativo, se abre hacia abajo.
Si el eje de la parábola es el eje X, la ecuación sería:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = ay^2
Parábolas con Vértice en Cualquier Punto
Cuando el vértice de la parábola no está en el origen, sino en un punto (h,k), las ecuaciones cambian un poco:
- Para una parábola vertical (que se abre hacia arriba o hacia abajo):
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (y-k) = a(x-h)^2 * También se puede escribir como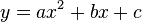 
, que es la forma general de una ecuación de segundo grado.
- Para una parábola horizontal (que se abre hacia la derecha o hacia la izquierda):
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x-h) = a(y-k)^2 * También se puede escribir como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x = ay^2 + by + c .
Ecuación con la Distancia Focal
La distancia focal (p) es la distancia entre el vértice y el foco. Podemos usarla en las ecuaciones:
- Para una parábola vertical con vértice en (0,0) y foco en (0,p):
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 = 4py (se abre hacia arriba) * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x^2 = -4py (se abre hacia abajo)
- Para una parábola horizontal con vértice en (0,0) y foco en (p,0):
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y^2 = 4px (se abre hacia la derecha) * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y^2 = -4px (se abre hacia la izquierda)
Si el vértice está en (h,k), las ecuaciones se ajustan así:
- Vertical: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (x-h)^2 = 4p(y-k)
- Horizontal: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (y-k)^2 = 4p(x-h)
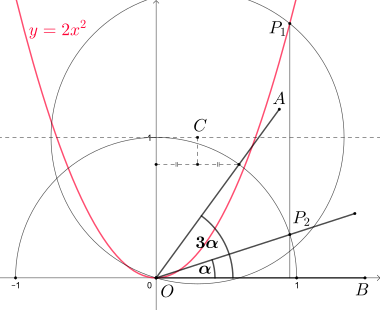
La Parábola como Trisectriz
¿Puede una parábola ayudar a dividir un ángulo en tres partes iguales?
Sí, la parábola puede usarse para dividir un ángulo en tres partes iguales, un problema que es imposible de resolver solo con regla y compás. Sin embargo, al usar una parábola como herramienta adicional, ¡sí se puede!
Este método fue descrito por el famoso matemático René Descartes en su libro La Géométrie en 1637. Es un ejemplo de cómo las curvas pueden ayudar a resolver problemas geométricos complejos.
Véase también
En inglés: Parabola Facts for Kids
- Ecuación de segundo grado
- Completar el cuadrado
- Paraboloide
- Elipse
- Hipérbola
- Sección cónica
- Esferas de Dandelin
