Coseno para niños
Datos para niños Coseno |
||
|---|---|---|
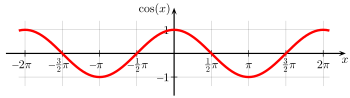 Gráfica de Coseno
|
||
| Definición | cos x | |
| Dominio | 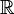 |
|
| Imagen | [-1,1] | |
| Cálculo infinitesimal | ||
| Derivada | -sen x | |
| Función primitiva | sen x + c | |
| Función inversa | arccos x | |
En matemáticas, el coseno es una función muy importante. Se usa mucho en trigonometría, que es la parte de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos.
El coseno se abrevia como cos. Es una función que se repite, es decir, es periódica. Su valor se repite cada 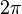 (o 360 grados). También es una función par, lo que significa que el coseno de un ángulo es igual al coseno de su ángulo negativo (por ejemplo, cos(30°) es igual a cos(-30°)).
(o 360 grados). También es una función par, lo que significa que el coseno de un ángulo es igual al coseno de su ángulo negativo (por ejemplo, cos(30°) es igual a cos(-30°)).
Contenido
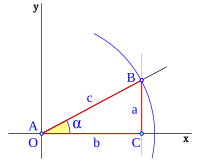
¿Qué es el Coseno en un Triángulo Rectángulo?
En un triángulo rectángulo (un triángulo con un ángulo de 90 grados), el coseno de uno de sus ángulos agudos (los que no son de 90 grados) se calcula dividiendo la longitud del cateto (lado) que está al lado del ángulo (el cateto adyacente) entre la longitud de la hipotenusa (el lado más largo, opuesto al ángulo de 90 grados).
Se escribe así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos\alpha = \frac{\text{cateto adyacente}}{\text{hipotenusa}}
Por ejemplo, si el cateto adyacente mide 3 unidades y la hipotenusa mide 5 unidades, el coseno del ángulo sería 3/5 = 0.6. Esta relación siempre es la misma para un ángulo dado, sin importar el tamaño del triángulo.
El Coseno y la Circunferencia Unitaria
Para entender el coseno de ángulos más grandes o negativos, usamos la circunferencia unitaria. Esta es una circunferencia con un radio de 1 unidad, centrada en el origen de un sistema de coordenadas.
Si dibujamos un ángulo desde el centro de esta circunferencia, el valor del coseno de ese ángulo es la coordenada 'x' del punto donde el lado final del ángulo toca la circunferencia. Como el radio es 1, la fórmula del triángulo rectángulo sigue funcionando.
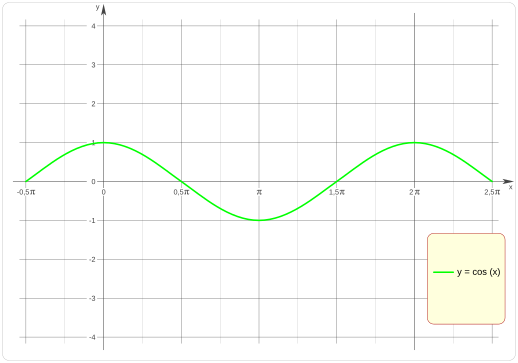
Gráfica de la Función Coseno
La función coseno se puede dibujar en una gráfica. La forma de esta gráfica es una onda suave y repetitiva, llamada sinusoide.
Esta gráfica nos muestra cómo cambia el valor del coseno a medida que el ángulo aumenta. El valor del coseno siempre estará entre -1 y 1.
Relaciones Importantes del Coseno
El coseno se relaciona con otras funciones trigonométricas, como el seno.
- Relación con el Seno: La gráfica del coseno es como la gráfica del seno, pero un poco desplazada.
: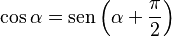
- Coseno de la Suma o Resta de Ángulos:
:Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos(\alpha + \beta) = \cos\alpha \cos\beta - \sen\alpha \sen\beta :Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos(\alpha - \beta) = \cos\alpha \cos\beta + \sen\alpha \sen\beta
- Coseno del Ángulo Doble:
: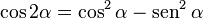
- Coseno del Ángulo Mitad:
:Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cos \bigg(\frac{\alpha}{2}\bigg)=\pm\sqrt{\frac{1+\cos\alpha}{2}} El signo (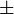 ) depende de en qué parte de la circunferencia se encuentre el ángulo.
) depende de en qué parte de la circunferencia se encuentre el ángulo.
Valores Exactos del Coseno para Ángulos Comunes
Para algunos ángulos, el valor del coseno se conoce con exactitud y es muy útil recordarlos:
| Ángulos en Radianes | Ángulos en Grados | Valor del Coseno |
|---|---|---|
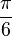 |
30° | 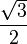 |
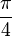 |
45° | 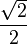 |
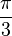 |
60° |  |
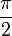 |
90° | 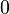 |
 |
180° | 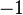 |
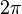 |
360° | 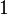 |
Recuerda que, como el coseno es una función par, el coseno de un ángulo negativo es el mismo que el de su versión positiva (por ejemplo, cos(-30°) = cos(30°)).
Usos del Coseno
El coseno se utiliza en muchas áreas, como:
- Física: Para describir ondas, movimientos oscilatorios y la descomposición de fuerzas.
- Ingeniería: En el diseño de estructuras, señales eléctricas y sistemas de sonido.
- Gráficos por Computadora: Para calcular sombras, iluminación y movimientos en animaciones 3D.
Galería de imágenes
Véase también
- Sinusoide
- Función
- Función par
- Trigonometría
- Funciones trigonométricas
Enlaces externos
- Weisstein, Eric W. «Coseno». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.