Razonamiento inductivo para niños
El razonamiento inductivo es una forma de pensar donde usamos lo que hemos observado en casos específicos para llegar a una idea general. La verdad de las ideas que usamos como punto de partida (llamadas premisas) hace que la conclusión sea probable, pero no la asegura al 100%.
Contenido
¿Qué es el razonamiento inductivo?
Un ejemplo sencillo
Imagina este ejemplo de razonamiento inductivo:
- Todos los cisnes que hemos visto hasta ahora son blancos.
- Por lo tanto, creemos que todos los cisnes son blancos.
Es importante saber que, aunque hayamos visto muchos cisnes blancos, siempre podría aparecer uno de otro color. A diferencia de otros tipos de razonamiento que garantizan la conclusión (como el razonamiento deductivo), el razonamiento inductivo nos permite aprender cosas nuevas y ampliar nuestro conocimiento, porque la conclusión añade información que no estaba explícitamente en las premisas. Por eso, es muy útil en la ciencia y en nuestra vida diaria.
Sin embargo, como las conclusiones no son totalmente seguras, surge una pregunta importante: ¿Cuándo podemos confiar en una conclusión inductiva? ¿Qué hace que un argumento inductivo sea bueno o malo? Estas preguntas forman parte de lo que se conoce como el Problema de la inducción, un tema que ha sido estudiado por muchos pensadores durante siglos.
Cómo funciona
La lógica inductiva se encarga de estudiar cómo podemos medir qué tan probable es que una conclusión sea verdadera. También nos da reglas para construir argumentos inductivos que sean "fuertes". Un argumento inductivo es fuerte cuando es muy poco probable que su conclusión sea falsa si las ideas de partida son verdaderas.
Tradicionalmente, se pensaba que la inducción era un método que iba "de lo particular a lo general". Esto significa que, a partir de observar muchos casos individuales o específicos, llegamos a una conclusión que se aplica a todos los casos de ese tipo. Por ejemplo, si observamos muchas veces que el agua hierve a 100 grados Celsius, podemos concluir que el agua siempre hierve a esa temperatura (a nivel del mar). Esto es diferente de la deducción, que va "de lo general a lo particular".
Detalles importantes
Hoy en día, la definición de inducción es un poco más amplia. Ya no se limita solo a ir de lo particular a lo general. Muchas veces, cuando sacamos conclusiones sobre cosas que podrían ser diferentes en el futuro (lo que llamamos "inferencia contingente"), se considera que estamos usando la inducción.
Aunque la inducción no puede ser "probada" de forma absoluta (como se discute en el Problema de la inducción), es una parte esencial del Método científico. Nos ayuda a expandir nuestro conocimiento sobre el mundo real. La gran ventaja de la inducción es que, si la usamos con cuidado, podemos corregir nuestras ideas si descubrimos nueva información.
Historia del razonamiento inductivo
Los inicios con Francis Bacon
El filósofo Francis Bacon fue uno de los primeros en la época moderna en explicar la importancia del método inductivo para el conocimiento científico. Él pensaba que, en lugar de solo deducir ideas de principios generales, debíamos observar el mundo y, a partir de esos hechos, construir nuestro conocimiento.
Bacon propuso un método con tres pasos:
- Tabla de presencia: Anotar todos los casos donde el fenómeno que estamos estudiando aparece, buscando la mayor variedad posible.
- Tabla de ausencia: Anotar casos donde el fenómeno no aparece, pero que son similares a los de la primera tabla. Esto ayuda a descartar lo que no es importante.
- Tabla de grados: Observar cómo el fenómeno cambia en intensidad.
Con estos pasos, Bacon creía que podíamos "eliminar" lo que no era relevante y llegar a la verdadera causa o explicación de un fenómeno.
David Hume y el problema de la inducción
Más tarde, el filósofo David Hume hizo una distinción importante: hay dos tipos de conocimiento. Uno es sobre las "relaciones de ideas" (como las matemáticas, donde las conclusiones son seguras) y otro es sobre las "cuestiones de hecho" (como lo que observamos en el mundo real). Para las cuestiones de hecho, solo la experiencia nos da información, y aquí es donde entra la inducción.
Para Hume, la inducción es un proceso mental: nuestra mente tiende a generalizar a partir de experiencias pasadas. Por ejemplo, si siempre hemos visto que el sol sale por la mañana, esperamos que siga saliendo. Pero Hume señaló que no hay una razón lógica que nos asegure que el futuro será como el pasado. Esto es el famoso Problema de la inducción.
Hume sugirió que la inducción se basa en la "costumbre". Si vemos que ciertos hechos se repiten, nos acostumbramos a esperar que sigan ocurriendo. Propuso dos tipos de inducciones:
- Por cercanía: Si siempre vemos que A ocurre antes que B, podemos pensar que A causa B.
- Por enumeración: Si cada vez que examinamos algo de tipo A, encontramos que tiene la característica B, esperamos que todos los A tengan la característica B. Por ejemplo, si todas las esmeraldas que hemos visto son verdes, esperamos que todas las esmeraldas sean verdes.
John Herschel y la búsqueda de causas
John Herschel, un científico, también se interesó en cómo descubrimos las causas de los fenómenos. Él pensaba que el proceso de encontrar las relaciones de causa y efecto es inductivo. Propuso principios para guiar esta búsqueda:
- Principio de clasificación: Agrupar cosas similares para encontrar características que comparten.
- Principio de comparación y contraste: Estudiar grupos ya formados para ver sus similitudes y diferencias.
Herschel también destacó la importancia de buscar:
- Conexiones causales: Encontrar la causa real de un fenómeno o una ley que siempre conecta dos fenómenos.
- Semejanzas: Si los hechos son similares en un aspecto, esa podría ser la causa.
- Intensidades: Observar cómo varía el fenómeno cuando la causa es más o menos intensa.
- Exclusiones: Si un posible factor causal no está presente cuando el fenómeno sí lo está, entonces no es la causa.
- Diferencias de antecedentes: Si dos situaciones son idénticas excepto por un factor, y ese factor cambia el resultado, entonces es la causa.
- Residuos: Si un fenómeno es complejo y ya explicamos algunas de sus causas, lo que queda por explicar (el "residuo") nos lleva a descubrir nuevas causas.
Los métodos de John Stuart Mill
John Stuart Mill propuso cinco métodos para encontrar las causas de los fenómenos, conocidos como los Métodos de Mill:
I. Método de la concordancia
Si en varios casos donde ocurre un fenómeno, solo hay una circunstancia en común, esa circunstancia es la causa. Por ejemplo, si varias personas se enferman después de comer en el mismo restaurante, y lo único que comieron en común fue un plato específico, ese plato podría ser la causa de la enfermedad.
II. Método de la diferencia
Si en dos situaciones que son idénticas en todo excepto en una circunstancia, el fenómeno ocurre en una y no en la otra, entonces esa única circunstancia diferente es la causa. Por ejemplo, si una planta crece bien con fertilizante y otra idéntica no crece bien sin él, el fertilizante es la causa del buen crecimiento.
III. Método de la concordancia y diferencia
Combina los dos anteriores para hacer la conclusión más fuerte.
IV. Método de los residuos
Si un fenómeno es complejo y sabemos que ciertas partes de él son causadas por factores conocidos, lo que queda del fenómeno (el "residuo") debe ser causado por factores aún no identificados.
V. Método de las variaciones concomitantes
Si un fenómeno cambia de una manera específica cada vez que otro fenómeno cambia de una manera específica, entonces es probable que estén relacionados como causa y efecto. Por ejemplo, si la temperatura sube y el helado se derrite más rápido, la temperatura es la causa de que el helado se derrita.
Mill creía que, para que la inducción funcione, debemos asumir que la naturaleza es "uniforme", es decir, que las mismas causas siempre producirán los mismos efectos. Este es el principio de la uniformidad de la naturaleza, que hoy se relaciona con el Principio de invariancia o Principio de simetría en la física, que dice que las leyes de la naturaleza son las mismas en todas partes y en todo momento.
Ejemplos de razonamiento inductivo
Ejemplo 1
- Tengo un automóvil que está hecho de hierro.
- El automóvil de mi vecino está hecho de hierro.
- El automóvil de mi padre está hecho de hierro.
- Por lo tanto, todos los automóviles están hechos de hierro.
(Esta conclusión es una generalización que podría ser falsa, ya que hay automóviles hechos de otros materiales).
Ejemplo 2
- El animal A, el animal B y el animal C están compuestos de células.
- El animal A, el animal B y el animal C son gatos.
- Los gatos son animales.
- Entonces, todos los gatos están compuestos de células.
(Aquí, la observación de algunos gatos nos lleva a una conclusión general sobre todos los gatos).
Ejemplo 3
- El hierro es un buen conductor de la electricidad.
- El cobre es un buen conductor de la electricidad.
- El hierro y el cobre son metales.
- Los metales son buenos conductores de la electricidad.
(Observamos propiedades en metales específicos y generalizamos a todos los metales).
Ejemplo 4
- Mi vecino tiene un perro guardián que ladra cuando se acerca un desconocido.
- Mi padre tiene un perro que avisa a su amo de la misma manera cuando se acercan extraños.
- Cuando los extraños entran en la propiedad del dueño, el perro avisa a su dueño.
- De este modo, todos los perros guardianes alertan a sus dueños cuando un extraño entra en su territorio.
(A partir de la observación de algunos perros guardianes, se llega a una conclusión general sobre su comportamiento).
La inducción como probabilidad
Charles Sanders Peirce y el circuito de investigación
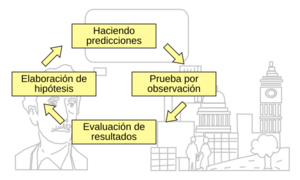
Charles Sanders Peirce propuso que el razonamiento se divide en tres tipos que trabajan juntos en la investigación:
- Abducción: Genera nuevas ideas o hipótesis.
- Deducción: Predice qué debería ocurrir si la hipótesis es correcta.
- Inducción: Verifica si las predicciones se cumplen mediante experimentos y observaciones.
Este "circuito" nos ayuda a reducir la incertidumbre. Si las observaciones no coinciden con las predicciones, se crean nuevas hipótesis. Si coinciden, se repiten las observaciones para aumentar la confianza en la hipótesis. La inducción, en este caso, no crea leyes, sino que confirma las hipótesis con grados de probabilidad.
Por ejemplo, si tenemos muchas cajas de canicas y queremos saber el porcentaje de canicas blancas. Sacamos 100 canicas de 20 cajas y encontramos que, en promedio, 3 de cada 100 son blancas. Por abducción, suponemos que el 3% de todas las canicas son blancas. La deducción predice que futuras muestras mostrarán una proporción similar. La inducción verifica esto, viendo cuántas observaciones confirman la predicción y con qué confianza.
Inducción como creencia razonable
Pensadores como John Maynard Keynes y Rudolf Carnap vieron la inducción como una forma de determinar el grado de "creencia razonable" o confianza que podemos tener en una hipótesis, basándose en la evidencia. Para Carnap, la lógica inductiva no busca descubrir leyes, sino determinar la probabilidad de una hipótesis a partir de la experiencia disponible.
La historia del pavo inductivista
Bertrand Russell (y luego Alan Francis Chalmers) contó la historia del "pavo inductivista" para mostrar los peligros de confiar solo en la inducción.
Un pavo en una granja notó que todos los días, a las nueve de la mañana, le daban de comer. Observó esto durante muchos días, en diferentes estaciones y climas, y llegó a la conclusión inductiva: "Siempre me dan de comer a las nueve de la mañana". Sin embargo, la víspera de Navidad, a las nueve de la mañana, en lugar de comida, le cortaron el cuello.
Esta historia nos enseña que, no importa cuántas veces algo haya sido cierto en el pasado, una conclusión inductiva puede ser falsa en el futuro. La ausencia de una prueba en contra no significa que algo sea imposible.
Nelson Goodman y el nuevo problema de la inducción
Nelson Goodman planteó un nuevo desafío a la inducción. Él señaló que cualquier observación puede describirse de muchas maneras diferentes. Por ejemplo, si todas las esmeraldas que hemos visto son verdes, podemos concluir que "todas las esmeraldas son verdes". Pero Goodman inventó una palabra, "verdul", que significa "verde si se examinó antes de cierto momento, y azul si no se examinó".
El problema es que, si todas las esmeraldas que hemos visto son verdes, también son "verdul". Entonces, ¿por qué preferimos la hipótesis "todas las esmeraldas son verdes" y no "todas las esmeraldas son verdul"? Goodman sugiere que usamos palabras o "predicados" que nos resultan familiares o que están "arraigados" en nuestra forma de pensar y hablar. Esto significa que nuestras categorías para entender el mundo son, en parte, una cuestión de costumbre.
Esto nos lleva a pensar que la justificación de las reglas de la inducción se basa en que se ajustan a cómo ya hacemos inferencias inductivas. Es un proceso de ajuste mutuo entre las reglas generales y las observaciones específicas.
Galería de imágenes
Ver también
- Razonamiento abductivo
- Razonamiento deductivo
- Analogía
- Inductivismo
- Inducción matemática
- Métodos de razonamiento
- Problema de la inducción
- Razonamiento analógico
Véase también
 En inglés: Inductive reasoning Facts for Kids
En inglés: Inductive reasoning Facts for Kids