Teoría de juegos para niños
Datos para niños Teoría de juegos |
||
|---|---|---|
| Campo de estudio | ||
 |
||
 |
||
La Teoría de Juegos es una parte de las matemáticas que estudia cómo las personas o grupos toman decisiones cuando sus resultados dependen de las decisiones de otros. Imagina que estás en un juego de mesa: tus movimientos afectan a los demás jugadores, y los suyos te afectan a ti. La Teoría de Juegos analiza estas "interacciones estratégicas" usando modelos especiales.
Esta teoría es muy útil en campos como la ciencia económica, la informática y la biología. También se aplica en la sociología, la politología (estudio de la política), la psicología y la filosofía. Ayuda a entender cómo las personas se comportan y toman decisiones en situaciones donde hay competencia o cooperación.
La Teoría de Juegos se divide en dos grandes grupos: Juegos No Cooperativos y Juegos Cooperativos. También se clasifican según cómo se juega, por ejemplo, si lo que uno gana es exactamente lo que otro pierde (Juegos de Suma Cero) o si todos pueden ganar o perder (Juegos de Suma No Cero).
Esta teoría fue desarrollada por John von Neumann y Oskar Morgenstern antes y durante la Guerra Fría. Al principio, se usó para entender la economía y la estrategia militar. Con el tiempo, se aplicó a la conducta animal y al desarrollo de las especies. También es importante en la inteligencia artificial y la cibernética.
Un "juego" en esta teoría es una situación donde hay un conflicto o competencia. Las decisiones de una persona influyen en las decisiones de las otras. El resultado final depende de todas las decisiones tomadas por todos los participantes.
Contenido
¿Cómo se representan los juegos?
Para estudiar los juegos, los expertos usan diferentes formas de representarlos.
El Dilema del Prisionero
El Dilema del Prisionero es un ejemplo famoso en la Teoría de Juegos. Imagina a dos personas que son interrogadas por separado por un problema. La policía les ofrece un trato a cada uno:
- Si uno confiesa y el otro no, el que confiesa sale libre y el otro recibe una pena larga.
- Si ambos confiesan, ambos reciben una pena media.
- Si ninguno confiesa, ambos reciben una pena corta por un delito menor.
El dilema es que, si cada uno piensa solo en su propio beneficio, lo más lógico es confesar. Pero si ambos confiesan, terminan con una pena media, que es peor que la pena corta que habrían recibido si ninguno hubiera confesado. Este juego muestra que a veces, buscar el beneficio individual no lleva al mejor resultado para el grupo.
Forma normal de un juego
| El jugador 2 elige izquierda | El jugador 2 elige derecha | |
|---|---|---|
| El jugador 1 elige arriba | 4, 3 | -1, -1 |
| El jugador 1 elige abajo | 0, 0 | 3, 4 |
La forma normal de un juego se representa con una tabla llamada "matriz de pagos". Esta tabla muestra:
- Quiénes son los jugadores.
- Qué opciones (estrategias) tiene cada jugador.
- Qué recompensa recibe cada jugador por cada combinación de estrategias.
En el ejemplo de la derecha, hay dos jugadores. El Jugador 1 elige una fila (arriba o abajo) y el Jugador 2 elige una columna (izquierda o derecha). Los números dentro de la tabla son las recompensas. El primer número es para el Jugador 1 y el segundo para el Jugador 2. Por ejemplo, si el Jugador 1 elige "arriba" y el Jugador 2 elige "izquierda", el Jugador 1 obtiene 4 y el Jugador 2 obtiene 3.
Cuando un juego se muestra en forma normal, se asume que los jugadores eligen sus estrategias al mismo tiempo. O al menos, no saben lo que el otro va a elegir antes de tomar su propia decisión.
Forma extensiva de un juego
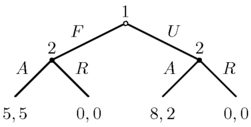
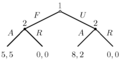
La forma extensiva se usa para juegos donde los jugadores toman decisiones en un orden específico. Se representan como "árboles de decisión". Cada punto donde un jugador toma una decisión se llama "nodo". Las líneas que salen de un nodo muestran las posibles acciones que el jugador puede tomar. Las recompensas finales se muestran al final de cada rama del árbol.
En el ejemplo de la derecha, el Jugador 1 mueve primero y elige "F" o "U". Luego, el Jugador 2 ve lo que eligió el Jugador 1 y decide entre "A" o "R". Si el Jugador 1 elige "U" y luego el Jugador 2 elige "A", el Jugador 1 obtiene 8 puntos y el Jugador 2 obtiene 2 puntos.
Tipos de juegos y ejemplos
La Teoría de Juegos clasifica los juegos en varias categorías para entenderlos mejor.
Juegos simétricos y asimétricos
| E | F | |
|---|---|---|
| E | 1, 2 | 0, 0 |
| F | 0, 0 | 1, 2 |
Un juego es simétrico si las recompensas de una estrategia dependen solo de lo que hacen los otros jugadores, no de quién es cada jugador. Es decir, si los jugadores intercambiaran sus roles, las recompensas por las mismas acciones seguirían siendo las mismas. Ejemplos son el dilema del prisionero y la caza del ciervo.
Los juegos asimétricos son aquellos donde las recompensas cambian si los jugadores intercambian sus roles. O donde los jugadores tienen diferentes opciones de estrategia. El ejemplo de la derecha es un juego asimétrico.
Juegos de suma cero y de suma distinta de cero
| A | B | C | |
|---|---|---|---|
| 1 | 30, -30 | -10, 10 | 20, -20 |
| 2 | 10, -10 | 20, -20 | -30, 30 |
En los juegos de suma cero, la ganancia de un jugador es exactamente la pérdida de otro. La suma total de las ganancias y pérdidas de todos los jugadores siempre es cero. Ejemplos clásicos son el ajedrez y el póker. Si tú ganas una partida de ajedrez, tu oponente pierde.
La mayoría de las situaciones en la vida real, como los negocios o la política, son juegos de suma distinta de cero. Esto significa que no siempre lo que uno gana es lo que otro pierde. Todos pueden ganar, o todos pueden perder. Por ejemplo, en un buen acuerdo de negocios, ambas partes pueden terminar mejor que antes. El dilema del prisionero es un juego de suma distinta de cero.
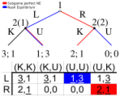
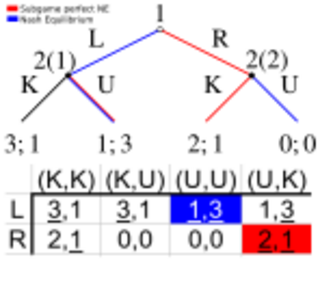
Equilibrio de Nash
El Equilibrio de Nash es un concepto muy importante en la Teoría de Juegos, nombrado por el matemático John Forbes Nash. Se da cuando cada jugador ha elegido la mejor estrategia posible, considerando lo que los otros jugadores han elegido. Una vez que se llega a un Equilibrio de Nash, ningún jugador tiene un motivo para cambiar su estrategia, porque ya está haciendo lo mejor que puede dadas las acciones de los demás.
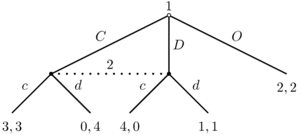
Juegos cooperativos
Un juego cooperativo es aquel donde los jugadores pueden formar acuerdos y trabajar juntos para lograr un objetivo común. Estos acuerdos pueden ser obligatorios. La teoría de los juegos cooperativos busca entender cómo se forman estos acuerdos y qué tan estables son.
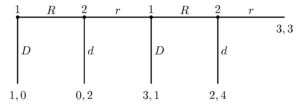
Juegos simultáneos y secuenciales
- Los juegos simultáneos son aquellos donde los jugadores toman sus decisiones al mismo tiempo, o sin saber lo que los otros han hecho antes. La forma normal (la tabla) se usa para representarlos.
- Los juegos secuenciales (o dinámicos) son aquellos donde los jugadores toman decisiones uno después del otro. Los jugadores posteriores tienen alguna información sobre las acciones previas. La forma extensiva (el árbol) se usa para representarlos.
Juegos de información perfecta
Un juego es de información perfecta si todos los jugadores conocen todos los movimientos que los demás han hecho antes. Esto solo ocurre en juegos secuenciales. Ejemplos son el ajedrez y el go.
No hay que confundir la información perfecta con la información completa. La información completa significa que cada jugador conoce las reglas, las estrategias posibles y las recompensas de todos los demás. El dilema del prisionero es un juego de información completa, pero no de información perfecta (porque las decisiones son simultáneas).
Aplicaciones de la Teoría de Juegos
La Teoría de Juegos es una herramienta matemática que se usa en muchas áreas diferentes.
Economía y negocios
Los economistas usan la Teoría de Juegos para analizar problemas como las subastas, la competencia entre empresas (como los duopolios u oligopolios) y los sistemas de votación. Buscan entender cómo las personas y las empresas toman decisiones para maximizar sus beneficios.
La teoría de juegos se usa de dos maneras principales en economía:
Descriptiva
Algunos investigadores creen que la Teoría de Juegos puede predecir cómo se comportarían las personas en situaciones reales. Sin embargo, a veces las personas no actúan de forma totalmente racional o egoísta, sino que también consideran el beneficio de un grupo más grande (altruismo). Por eso, esta aplicación tiene sus límites.
Normativa
| Cooperar | Traicionar | |
|---|---|---|
| Cooperar | 2 2 |
0 3 |
| Traicionar | 3 0 |
1 1 |
Otros ven la Teoría de Juegos como una guía de cómo las personas deberían comportarse para obtener los mejores resultados. Por ejemplo, si el Equilibrio de Nash es la mejor respuesta a las acciones de otros, seguirlo parece lo más lógico. Sin embargo, el Dilema del Prisionero muestra que a veces, si todos buscan solo su propio beneficio, el resultado final es peor para todos.
Psicología
La Teoría de Juegos se usa para estudiar cómo las personas toman decisiones, especialmente en situaciones donde se distribuyen recursos. Ayuda a entender cómo la confianza y la forma en que percibimos a los demás influyen en nuestras elecciones.
Biología
| Halcón | Paloma | |
|---|---|---|
| Halcón | (V-C)/2 (V-C)/2 |
V 0 |
| Paloma | 0 V |
V/2 V/2 |
En biología, las recompensas de los juegos se interpretan como la capacidad de un organismo para sobrevivir y reproducirse (adaptación). Se usa para entender la evolución biológica, como la proporción de machos y hembras en una especie. También ayuda a explicar cómo surge la comunicación animal y cómo los animales compiten por territorios.
Informática y lógica
La Teoría de Juegos es importante en la lógica y la informática. Se usa para modelar cómo interactúan los programas de computadora entre sí.
Ciencia política
En la ciencia política, la Teoría de Juegos ayuda a entender cómo los gobiernos y los grupos de interés toman decisiones. Por ejemplo, se usa para analizar las negociaciones y las decisiones públicas.
Derecho Penal y Criminología
Recientemente, la Teoría de Juegos se está usando para entender la responsabilidad de las empresas en ciertos problemas y para crear programas que ayuden a prevenir situaciones negativas. Ayuda a analizar cómo los individuos dentro de una organización toman decisiones y cómo estas decisiones interactúan entre sí.
Filosofía
| Ciervo | Liebre | |
|---|---|---|
| Ciervo | 3, 3 | 0, 2 |
| Liebre | 2, 0 | 2, 2 |
En filosofía, la Teoría de Juegos se ha usado para entender conceptos como la convención (acuerdos sociales) y el conocimiento común. También se ha explorado cómo la moralidad y el interés personal se relacionan, usando juegos como el dilema del prisionero y la caza del ciervo.
Música
Algunos compositores, como Iannis Xenakis, han usado ideas de la Teoría de Juegos en sus obras musicales, como Duel o Stratégie.
Historia de la Teoría de Juegos
| Año | Acontecimiento |
|---|---|
| 1713 | James Waldegrave hace la primera demostración matemática para un caso de dos jugadores. |
| 1838 | Antoine Augustin Cournot publica una solución teórica para dos jugadores. |
| 1928 | John von Neumann presenta artículos importantes sobre el tema. |
| 1944 | John von Neumann y Oskar Morgenstern publican Theory of Games and Economic Behavior. |
| 1950 | Albert W. Tucker presenta el "dilema del prisionero". John Forbes Nash desarrolla el equilibrio de Nash. |
| 1965 | Reinhard Selten introduce el concepto de equilibrios perfectos del subjuego. |
| 1967 | John Harsanyi desarrolla conceptos de información completa y juegos bayesianos. |
| 1982 | En biología, John Maynard Smith introduce la estrategia evolutivamente estable. |
| 1994 | John Harsanyi, John Forbes Nash y Reinhard Selten ganan el Premio en Ciencias Económicas en memoria de Alfred Nobel. |
| 2012 | Lloyd Stowell Shapley y Alvin E. Roth ganan el Premio en Ciencias Económicas en memoria de Alfred Nobel. |
La primera vez que se habló de la Teoría de Juegos fue en una carta de James Waldegrave en 1713. Sin embargo, no fue hasta 1838 que Antoine Augustin Cournot publicó un análisis más formal.
El campo de estudio de la Teoría de Juegos realmente comenzó con los trabajos de John von Neumann en 1928. Más tarde, en 1944, publicó un libro muy importante con Oskar Morgenstern llamado Theory of Games and Economic Behavior. Este libro mostraba cómo encontrar soluciones para juegos de suma cero con dos personas.
En 1950, Albert W. Tucker presentó formalmente el dilema del prisionero. Ese mismo año, John Forbes Nash desarrolló el concepto del equilibrio de Nash, que es una estrategia óptima para juegos con muchos jugadores.
Durante la década de 1950, la Teoría de Juegos creció mucho. Se desarrollaron conceptos clave y se empezó a aplicar en la filosofía y la ciencia política.
En los años siguientes, otros investigadores como Reinhard Selten y John Harsanyi hicieron contribuciones importantes. Por sus trabajos, John Harsanyi, John Forbes Nash y Reinhard Selten ganaron el Premio en Ciencias Económicas en memoria de Alfred Nobel en 1994.
En la década de 1970, la Teoría de Juegos se aplicó mucho a la biología, gracias al trabajo de John Maynard Smith y su idea de la estrategia evolutivamente estable.
Más tarde, otros expertos como Thomas Schelling, Robert Aumann, Roger Myerson, Lloyd Stowell Shapley y Alvin E. Roth también recibieron el Premio en Ciencias Económicas en memoria de Alfred Nobel por sus aportaciones a este campo.
Galería de imágenes
Véase también
 En inglés: Game theory Facts for Kids
En inglés: Game theory Facts for Kids
- Teoría de los juegos de rol
- Dinámica de sistemas
- Sistema dinámico
- Sistema complejo